Межа послідовності комплексних чисел

Послідовністю комплексних чисел називається перенумерована нескінченна множина комплексних чисел.

Надалі послідовність комплексних чисел ми будемо позначати символом . Комплексні числа , що утворять послідовність , називаються її елементами.

Число z називається межею послідовності , якщо для будь-якого позитивного числа можна вказати такий номер , починаючи з якого всі елементи цієї послідовності задовольняють нерівності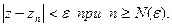

Послідовність , що має межу z, називається збіжною до числа z, що записується у вигляді .

Для геометричної інтерпретації граничного переходу в комплексній області зручним виявляється поняття околиці крапки комплексної площини.

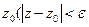Множина точок z комплексної площини, що лежать усередині окружності радіуса із центром у крапці ), називається - околицею точки .

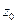Із цього визначення треба, що крапка z є межею збіжної послідовності , якщо в кожній - околиці крапки z лежать всі елементи цієї послідовності, починаючи з деякого номера, що залежить від .

Оскільки кожне комплексне число характеризується парою дійсних чисел 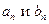, то послідовності комплексних чисел відповідають дві послідовності дійсних чисел й , складені відповідно з дійсних і мнимих частин елементів послідовності .

Має місце наступне твердження.

Теорема. Необхідною й достатньою умовою збіжності послідовності є збіжність послідовностей дійсних чисел й .

Послідовність називається обмеженою, якщо існує таке позитивне число М, що для всіх елементів цієї послідовності має місце нерівність .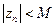

Основна властивість обмеженої послідовності характеризує наступна теорема.

Теорема. Із усякої обмеженої послідовності можна виділити збіжну підпослідовність.

При дослідженні збіжності послідовності в багатьох випадках зручним виявляється необхідна й достатня ознака збіжності послідовності, відомий за назвою критерію Коші.

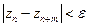Критерій Коші. Послідовність сходиться тоді й тільки тоді, коли для будь-якого > 0 можна вказати таке N(), що при 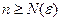й для будь-якого номера .

Дата добавления: 2014-12-07