Перетворення (перетвір) Лапласа. Оригінал і зображення

Операційне числення

Операційне (символічне) числення широко застосовується на практиці при розв¢язанні різних задач науки і техніки. Особливо широке застосування воно має при дослідженні перехідних процесів у лінійних фізичних системах електротехніки, автоматики, радіотехніки і телемеханіки.

Сучасний математичний апарат операційного числення дозволяє розв¢язувати задачі, математичними моделями яких є системи лінійних диференціальних рівнянь (звичайних і з частинними похідними), різницеві і диференційно-різницеві рівняння та деякі типи інтегральних рівнянь. Велика універсальність операційного числення при розв¢язанні задач пояснюється можливістю отримати їх розв¢язки найбільш раціональним шляхом.

Операційне числення засноване на так званому перетворенні Лапласа (операторові спеціального виду)

, (3.1)

яке є невласним інтегралом першого роду.

Тут , взагалі кажучи, комплексна функція-оригінал дійсного аргументу 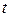, що найчастіше інтерпретується як час, а тому 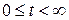. Функція 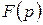комплексного аргументу 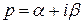, обумовлена інтегралом Лапласа (3.1), називається зображенням за Лапласом функції-оригіналу .

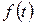Той факт, що функція 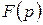є зображенням функції-оригіналу 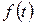символічно записується так:

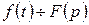або .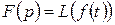

Функцією-оригіналом називається функція 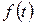, яка задовольнює наступні умови:

а) 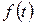інтегрована на будь-якому кінцевому інтервалі осі ;

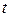б) для всіх від¢ємних : ;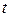

в) 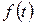зростає не швидше показникової (експоненціальної) функції, тобто існують такі дійсні сталі і , що

Умова а) означає, що функція – оригінал 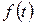на будь-якому кінцевому відрізку 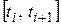додатної півосі задовольняє умови Діріхле, тобто, по-перше, обмежена, по-друге, або безперервна, або має лише кінцеве число точок розриву першого роду, і, по-третє, має кінцеве число екстремумів. При цьому за значення оригіналу 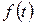у всякій його точці розриву 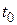першого роду приймається напівсума його граничних значень ліворуч і праворуч від цієї точки:

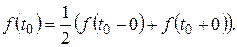
Так, зокрема, у силу умови б) за значення оригіналу в точці береться права границя:

.

Умова б) виправдана тим, що для фізики і техніки зовсім байдуже як поводяться об'єкти, що розглядаються до деякого початкового моменту часу, прийнятого за момент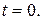

Умова в) накладає обмеження на характер росту оригіналу 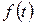, тобто, вимагає щоб 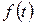при 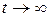зростала за абсолютною величиною не швидше показової експоненціальної функції, тому число називається показником росту оригіналу .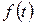

Більшість функцій, що зустрічається на практиці, задовольняє умові в). Як приклад функцій, для яких умова в) не виконується, можна навести функцію .

Далі показується, що обмеження в) накладається на оригінал 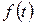для забезпечення збіжності інтегралу Лапласа (3.1).

Справді, якщо оригінал 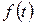задовольнює умову в) і 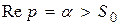, то інтеграли у правій частині рівності

збігаються абсолютно.

Спочатку оцінюється перший з цих інтегралів.

Аналогічно оцінюється і другий інтеграл.

Таким чином, для будь-якої функції-оригіналу 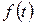зображення 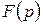визначене в напівплощині і є в цій напівплощині аналітичною функцією.

Дата добавления: 2014-12-07