Приклад 2. 3 страница

3.2 Класифікація математичних моделей

Математичні моделі класифікуються:

– по приналежності до ієрархічного рівня: на моделі мікрорівня, макрорівня, метарівня.

Математичні моделі на мікрорівні процесу відображають фізичні процеси, що протікають, наприклад, при різанні металів. Вони описують процеси на рівні переходу (проходу).

Математичні моделі на макрорівні процесу описують технологічні процеси.

Математичні моделі на метарівні процесу описують технологічні системи (ділянки, цехи, підприємство в цілому).

– по характеру властивостей об'єкту, що відображаються, моделі можна класифікувати на структурних і функціональних.

Модель структурна, – якщо вона представима структурою даних або структурами даних і відносинами між ними; наприклад, структурною моделлю може служити опис (табличний, графовий, функціональний або інше) структури екосистеми. У свою чергу, структурна модель може бути ієрархічною або мережевою.

Модель ієрархічна (деревовидна), – якщо представима деякою ієрархічною структурою (деревом); наприклад, для вирішення завдання знаходження маршруту в дереві пошуку можна побудувати деревовидну модель, приведену на рис.3.2

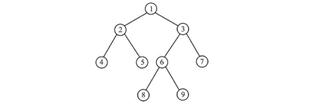
Рис.3.2 Модель ієрархічної структури

Модель мережева, – якщо вона представима деякою мережевою структурою. Наприклад, будівництво нового будинку включає операції, приведені в нижченаведеній таблиці 3.1.

Таблиця 3.1

№ операц	Операція	Час викон. (дні)	Попередні операції	Дуги графа
	Розчищення ділянки		немає	-
	Закладка фундаменту		Розчищення ділянки (1)	1-2
	Зведення стін		Закладка фундамен. (2)	2-3
	Монтаж електрики		Зведення стін (3)	3-4
	Штукатурні роботи		Монтаж електрики (4)	4-5
	Благоустрій території		Зведення стін (3)	3-6
	Оздоблювальні роботи		Штукатурні роботи (5)	5-7

Ці операції можна представити у вигляді мережевої моделі, приведеної на

рис. 3.3.

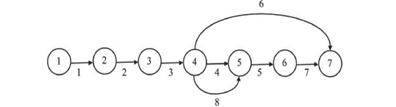
Рис. 3.3 Мережевий графік будівництва робіт

Модель функціональна, – якщо вона представима у вигляді системи функціональних співвідношень. Наприклад, закон Ньютона і модель виробництва товарів – функціональні.

– за способом представлення властивостей об'єкту моделі діляться на аналітичні, чисельні, алгоритмічні і імітаційні.

Аналітичними математичними моделями є явні математичні вирази вихідних параметрів як функцій від параметрів вхідних і внутрішніх і мають єдині рішення за будь-яких початкових умов. Наприклад, процес різання (точіння) з погляду сил, що діють, є аналітичною моделлю. Також квадратне рівняння, що має одне або декілька рішень, буде аналітичною моделлю.

Модель буде чисельною, якщо вона має рішення за конкретних початкових умов (диференціальні, інтегральні рівняння).

Модель алгоритмічна, – якщо вона описана деяким алгоритмом або комплексом алгоритмів, що визначає її функціонування і розвиток. Введення даного типу моделей (дійсно, здається, що будь-яка модель може бути представлена алгоритмом її дослідження) цілком обгрунтоване, оскільки не всі моделі можуть бути досліджені або реалізовані алгоритмічно. Наприклад, моделлю обчислення суми нескінченного убуваючого ряду чисел може служити алгоритм обчислення кінцевої суми ряду до деякої заданої міри точності. Алгоритмічною моделлю кореня квадратного з числа Х можеслужити алгоритм обчислення його наближеного скільки завгодно точного значення по відомій рекурентній формулі.

Модель імітаційна, – якщо вона призначена для випробування або вивчення можливих шляхів розвитку і поведінки об'єкту шляхом варіювання деяких або всіх параметрів моделі, наприклад модель економічної системи виробництва товарів двох видів. Таку модель можна використовувати як імітаційної, з метою визначення і варіювання загальної вартості залежно від тих або інших значень об'ємів вироблюваних товарів.

– за способом отримання моделі діляться на теоретичні і емпіричні.

Теоретичні математичні моделі створюються в результаті дослідження об'єктів (процесів) на теоретичному рівні. Наприклад, існують вирази для сил різання, отримане на основі узагальнення фізичних законів. Але вони неприйнятні для практичного використання, оскільки дуже громіздкі і не зовсім адаптовані до реальних процесів обробки матеріалів.

Емпіричні математичні моделі створюються в результаті проведення експериментів (вивчення зовнішніх проявів властивостей об'єкту за допомогою вимірювання його параметрів на вході і виході) і обробки їх результатів методами математичної статистики.

– за формою представлення властивостей об'єкту моделі діляться на логічні, теоретико-множинні і графові.

Модель логічна, якщо вона представима предикатами, логічними функціями, наприклад, сукупність двох логічних функцій може служити математичною моделлю однорозрядного суматора.

Модель теоретико-множинна, – якщо вона представима за допомогою деяких множин і відносин приналежності ним і між ними.

Модель графова, – якщо вона представима графом або графами і відносинами між ними.

3.3 Побудова і аналіз математичних моделей

Початковим пунктом для побудови моделі, як правило, буває деяка емпірична реальна картина явища, яка висуває перед дослідником задачу, на яку потрібно знайти відповідь.

Основні етапи побудови і аналізу конкретних моделей представлено на рис. 3.4. Опишемо стисло ці етапи.

Етап 1. При з'ясуванні і постановці задачі на фізичному рівні проходить процес схематизації і ідеалізація явища (рис. 3.4), тобто виділення його істотних особливостей. Деякі риси явища можуть виявитися важливими, інші - неістотними.

Етап 2. Після виявлення істотних чинників потрібні дані перекладаються мовою математичних понять і величин: складаються системи визначальних параметрів явища, формулюються співвідношення між величинами і параметрами.

Це найважча стадія процесу моделювання. Тут досліднику доводиться часто спиратися на фундаментальні фізичні закони.

Етапи 3,4. Після побудови моделі (етап 3) слід проводити перевірку адекватності моделі явищу і логічній несуперечності або коректності постановки задачі. Так, можна використовувати вельми просте і завжди ефективне правило перевірки фізичної розмірності всіх членів рівнянь.

Рис.3.4 Етапи побудови і аналізу моделей

Етапи 3,4. Після побудови моделі (етап 3) слід проводити перевірку адекватності моделі явищу і логічній несуперечності або коректності постановки задачі. Так, можна використовувати вельми просте і завжди ефективне правило перевірки фізичної розмірності всіх членів рівнянь.

Етапи 5,6. Перевіряється справедливість моделі і результатам рішення теоретичної задачі відповідно до математичної моделі і зіставлення їх з реальною ситуацією, яка вивчається. Глибина віддзеркалення моделлю дійсності залежить від цілей дослідження.

Вид математичної моделі визначається не тільки природою реального об'єкту, але і тими завданнями, для вирішення яких будується модель, а також необхідною точністю їх рішень. Тому необхідні дослідження отриманої моделі з метою визначення області її найбільш ефективного використання при рішенні інженерної задачі і встановлення меж зміни змінних, в яких вона справедлива.

Розглянемо як приклад побудову моделі Сонячної системи.

Спостереження за зоряним небом почалися ще в глибокій старовині. Первинний аналіз цих спостережень дозволив виділити планети зі всієї різноманітності небесних світил. Отже, першим кроком було виявлення об'єкту дослідження. Іншим кроком стало виявлення закономірності руху планет, тобто «аксіом» гіпотетичної моделі. З початку була створена модель Птолемея (II ст. до н.е.) – геоцентрична модель. У ній Сонце і планети рухалися навколо Землі. Ці рухи описувалися за допомогою правил (формул), але у міру накопичення результатів спостереження вони постійно ускладнювалися.

М.Копернік в 1543 роцізапропонував принципово нову модель Сонячної системи - геліоцентричну. У ній всі планети обертаються навколо Сонця. Проте ця модель ще не була математичною, поскільки не було параметрів моделі (швидкостей руху планет, параметрів орбіт і т.д).

У XVII ст. Кеплерсформулював закон руху планет. Вони описували кінематику руху кожної планети окремо, не стосуючись причин, що викликають це рух.

І. Ньютон в 2 - й половині XVII століттязапропонував динамічну модель Сонячної системи. Вона базувалася на відкритому ним законі усесвітнього тяжіння. Динамічна модель Ньютона узгоджувалася з кінематичною моделлю Кеплера.

Проте в 40годах XIX ст.результатыдинамічній моделі почали суперечити накопичені результати спостережень. Наприклад, рух планети Уран відхилявся від теоретично обчисленного руху на моделі. Це дозволило Леверьє в 1846г. передбачити нову планету – Нептун, яка впливає на рух планети Уран. Пізніше в тому місці, на яке указував Леверьє, дійсно була відкрита планета Нептун.

Так само була передбачена і пізніше відкрита в 1930р планета Плутон. Одночасно з відкриттям нових планет, удосконалювалася і модель Сонячної системи.

3.4 Компонентні і топологічні рівняння модельованого об'єкту.

Поведінку більшості фізичних систем можна охарактеризувати за допомогою фазових змінних. Фазова змінна (ФЗ) -цевеличина, що характеризує фізичний або інформаційний стан модельованого об'єкту. Так, в електричній системі ФЗ це струми і напруги, а в механічній системі – сили і швидкості.

Закони функціонування елементів системи задаються компонентними рівняннями. Вони описують зв'язок ФЗ різного типу для кожного елементу системи. Компонентні рівняння- це рівняння математичних моделей елементів системи. Вони можуть бути лінійними, нелінійними, алгебраїчними, диференціальними або інтегральними.

Кожен елемент модельованого об'єкту повинен мати компонентне рівняння. Для більшості елементів такі рівняння вже отримані, їх використовують при моделюванні. Наприклад, в гідравліці для дроселя є аналітичний вираз, який зв'язує витрату і тиск:

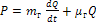, де Р – тиск, Па;

Q – витрата, м³ /c;

m _г ^– коефіцієнт маси, кг/м⁴ ;

μ _г – коефіцієнт демпфування, Н*с/м.

Зв'язок між однорідними ФЗ, які відносяться до різних елементів в підсистемах, встановлюється топологічними рівняннями. Вони відображають топологію взаємозв'язків елементів. Їх отримують на основі даних про структуру системи. Приклади топологічних рівнянь: у електричних системах – рівняння на основі законів Кірхгофа; у механічних системах – рівняння, що відображають принципи Д.Аламбераі додавання швидкостей і так далі. Очевидно, що процедура розробки топологічних рівнянь виконується для кожного моделюючого об'єкту, оскільки структури об'єктів різні.

Математичну модель системи отримують об'єднанням компонентних і топологічних рівнянь цієї системи.

4 Математичні схеми моделювання систем

4.1 Безперервно- детерміновані моделі ( D - схеми)

Розглянемо особливості безперервно-детермінованого підходу на прикладі використання в якості математичних моделей диференціальних рівнянь.

Зазвичай в таких математичних моделях незалежною змінною, від якої залежать невідомі шукані функції, служить час t. Тоді математичне співвідношення для детермінованих систем в загальному вигляді буде

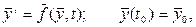
де y ' = d y /dt, y = (y₁, у₂,..., у_п) и f = (f₁,f₂,…,f_n) - n -мірні вектори; f( y, t ) — вектор-функція, яка визначена на деякій (п+ 1) - мірній (у, t) множині і є безперервною.

Оскільки математичні схеми такого вигляду відображають динаміку системи, що вивчається, тобто її поведінку в часі, то вони називаються

D - схемами (англ. dynamic).

У простому випадку звичайне диференціальне рівняння має вигляд

Найбільш важливе для системотехніки застосування D-схем як математичний апарат в теорії автоматичного управління.

Для ілюстрації особливостей побудови і застосування D-схем розглянемо простий приклад формалізації процесу функціонування двох елементарних систем різної фізичної природи: механічної S_М (коливання маятника) і електричної S_K (коливальний контур).

Процес малих коливань маятника описується звичайним диференціальним рівнянням

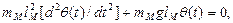
де т_м, l_М — маса і довжина підвісу маятника; g — прискорення вільного падіння; θ(t) - кут відхилення маятника у момент часу t.

З цього рівняння вільного коливання маятника можна знайти оцінки характеристик, які цікавлять. Наприклад, період коливання маятника

Аналогічно, процеси в електричному коливальному контурі описуються звичайним диференціальним рівнянням

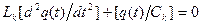
де L_K, С_K — індуктивність і ємкість конденсатора; q (t) — заряд конденсатора у момент часу t.

З цього рівняння можна отримати різні оцінки характеристик процесу в коливальному контурі. Наприклад, період характеристичних коливань

Очевидно, що, ввівши позначення h_o = m_M l ²_M = L_K, h₁ = 0, h₂ = m_M g l_M = 1/С_K, θ(t) = q(t)=z(t), отримаємо звичайне диференціальне рівняння другого порядку, що описує поведінку цієї замкнутої системи:

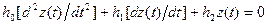(4.1)

де h₀, h₁ , h₂ — параметри системи; z(t) — стан системи у момент часу t.

Таким чином, поведінка цих двох об'єктів може бути досліджена на основі загальної математичної моделі (4.1). Крім того, необхідно відзначити, що поведінка однієї з систем може бути проаналізоване за допомогою іншої. Наприклад, поведінка маятника (системи S_М) може бути вивчене за допомогою електричного коливального контура (системи S_К).

Якщо система S, що вивчається, тобто маятник або контур, взаємодіє із зовнішнім середовищем Е, тоз'являється вхідна дія x(t) ( зовнішня сила для маятника і джерело енергії для контура) і безперервно-детермінована модель такої системи матиме вигляд

З погляду загальної схеми математичної моделі х(t) є вхідною (управляючою) дією, а стан системи S в даному випадку можна розглядати як вихідну характеристику, тобто вважати, що вихідна змінна співпадає із станом системи в даний момент часу у = z.

4.2 Безперервно- стохастичні моделі ( Q - схеми)

Особливості безперервно-стохастичного підходу розглянемо на прикладі використання в якості типових математичних схем систем масового обслуговування (англ. queueing system), які називатимемо Q-схемами. Системи масового обслуговування є класом математичних схем, розроблених в теорії масового обслуговування і різних застосуваннях для формалізації процесів функціонування систем, які за своєю суттю є процесами обслуговування. Системи масового обслуговування - це такі системи, в які у випадкові моменти часу поступають заявки на обслуговування. Заявки, що при цьому поступили, обслуговуються за допомогою каналів обслуговування, що є у розпорядженні системи.

В якості процеса обслуговування можуть бути представлені різні по своїй фізичній природі процеси функціонування економічних, виробничих, технічних і інших систем, наприклад потоки постачань продукції деякому підприємству, потоки деталей і комплектуючих виробів на складальному конвеєрі цеху, заявки на обробку інформації ЕОМ від віддалених терміналів і так далі. При цьому характерною для роботи таких об'єктів є випадкова поява заявок (вимог) на обслуговування і завершення обслуговування у випадкові моменти часу, тобто стохастичний характер процесу їх функціонування. Зупинимося на основних поняттях масового обслуговування, необхідних для використання Q-схем, якпри аналітичному, так і при імітаційному.

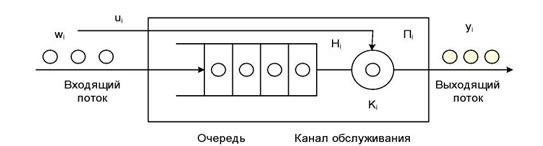
У будь-якому елементарному акті обслуговування можна виділити дві основні складові: очікування обслуговування заявкою і власне обслуговування заявки. Це можна зобразити у вигляді деякого i-го приладу обслуговування П_i (рис. 4.1), що складається з накопичувача заявок H_i (черга), і каналу обслуговування заявок (або просто каналу) K_i. На кожен елемент приладу обслуговування П_i поступають потоки подій: у накопичувач H_i — потік заявок w_i, на канал K_i — - потік обслуговувань u_i.

Потоком подій називається послідовність подій, що відбуваються одне за іншим в якісь випадкові моменти часу. Розрізняють потоки однорідних і неоднорідних подій. Потік подій називається однорідним, якщо він характеризується тільки моментами надходження цих подій (моментами появи) і задається послідовністю

{t_n} = { 0 ≤ t₁ ≤ t₂ ≤... ≤ t_n ≤... }, де t_n — момент настання n-ї події — ненегативне дійсне число. Однорідний потік подій також може бути заданий у вигляді послідовності проміжків часу між n-м і (n-1) -м подіями {τ_n}.

Рис. 4.1 Прилад обслуговування

Потоком неоднорідних подій називається послідовність (t_n, f_n), де t_n -вызывающие моменти; f_n — набір ознак події. Наприклад, стосовно процесу обслуговування для неоднорідного потоку заявок можуть бути задані приналежність до того або іншого джерела заявок, наявність пріоритету, можливість обслуговування тим або іншим типом каналу і тому подібне

Приклад потоку подій приведений на рис. 4.2, де позначене T_j - інтервал між подіями (випадкова величина); T_H - час спостереження, T_с - момент здійснення події.

Рис. 4.2 Схема потоку подій

Якщо T_j = const або визначено якою-небудь формулою T_j = f(T_j-1), то потік називається детермінованим. Інакше потік називається випадковим.

Заявки, обслужені каналом і заявки, що покинули прилад, з різних причин необслуженими (наприклад, через переповнювання накопичувача), утворюють вихідний потік. Інтервали часу між моментами виходу заявок утворюють підмножину вихідних змінних.

Процес функціонування пристрою обслуговування, можна представити як процес зміни станів його елементів в часі z_i(t). Перехід в новий стан системи означає зміна кількості заявок, які в нім знаходяться (у пристрої обслуговування і в черзі).

У практиці моделювання систем, що мають складніші структурні зв'язки і алгоритми поведінки, для формалізації використовуються не окремі прилади обслуговування, а Q-схемы, що утворюються композицією багатьох елементарних приладів обслуговування (мережі масового обслуговування). Якщо канали різних приладів обслуговування сполучені паралельно, то має місце багатоканальне обслуговування (багатоканальна Q-схема), а якщо прилади і їх паралельні композиції сполучені послідовно, то має місце багатофазне обслуговування (багатофазна Q-схема). Таким чином, для завдання Q-схемы необхідно використовувати оператор сполучення R, що відображає взаємозв'язок елементів структури (каналів і накопичувачів) між собою.

Зв'язки між елементами Q-схемы зображають у вигляді стрілок (ліній потоку, що відображають напрям руху заявок). Розрізняють розімкнені і замкнуті Q-схеми. У розімкненій Q-схемі вихідний потік обслужених заявок не може знову поступити на який-небудь елемент, тобто зворотній зв'язок відсутній, а в замкнутих Q-схемах єзворотні зв'язки, по яких заявки рухаються в напрямі, зворотному руху вхід-вихід.

Для завдання Q-схемы також необхідно описати алгоритми її функціонування, які визначають набір правил поведінки заявок в системі в різних неоднозначних ситуаціях. Залежно від місця виникнення таких ситуацій розрізняють алгоритми (дисципліни) очікування заявок в накопичувачі (черзі)і обслуговування заявок каналом кожного елементарного обслуговуючого приладу Q-схемы. Неоднорідність заявок, що відображає процес в тій або іншій реальній системі, враховується за допомогою введення класів пріоритетів.

Виходячи з правил вибору заявок з накопичувача H_i на обслуговування каналом K_i можна виділити відносні і абсолютні пріоритети. Відносний пріоритет означає, що заявка з вищим пріоритетом, що поступила в накопичувач, чекає закінчення обслуговування попередньої заявки каналом, і лише після цього займає канал. Абсолютний пріоритет означає, що заявка з вищим пріоритетом, що поступила в накопичувач перериває обслуговування каналом заявки з нижчим пріоритетом і сама займає канал (при цьому витіснена з каналу обслуговування заявка може або покинути систему, або може бути знову записана на якесь місце в накопичувач).

4.3 Дискретно-детерміновані моделі (F - схеми)

Особливості дискретно-детермінованого підходу на етапі формалізації процесу функціонування систем розглянемо на прикладі використання в якості математичного апарату теорії автоматів. Теорія автоматів - це розділ теоретичної кібернетики, в якому вивчаються математичні моделі - автомати. На основі цієї теорії система представляється у вигляді автомата, що переробляє дискретну інформацію і що міняє свої внутрішні стани лише в допустимі моменти часу. Поняття «автомат» варіюється залежно від характеру систем, що конкретно вивчаються, від прийнятого рівня абстракції і доцільного ступеня спільності.

Автомат можна представити як деякий пристрій (чорний ящик), на який подаються вхідні сигнали і знімаються вихідні і який може мати деякі внутрішні стани. Кінцевим автоматом називається автомат, у якого безліч внутрішніх станів і вхідних сигналів (а отже, і безліч вихідних сигналів) є кінцевими множинами.

Абстрактно кінцевий автомат (англ. finite automata) можна представити як математичну схему (F-схему), що характеризується шістьма елементами: кінцевою множиною X вхідних сигналів (вхідним алфавітом); кінцевою множиною Y вихідних сигналів (вихідним алфавітом); кінцевою множиною Z внутрішніх станів (внутрішнім алфавітом або алфавітом станів); початковим станом z₀, z_o є Z; функцією переходів φ (z, х); функцією виходів ψ (z, x). Автомат, що задається F-схемой: F=(Z, X, Y, φ, ψ, z_o) - функціонує в дискретному автоматному часі, моментами якого є такти, тобто рівні інтервали часу, що примикають один до одного, кожному з яких відповідають постійні значення вхідного і вихідного сигналів і внутрішні стани. Позначимо стан, а також вхідний і вихідний сигнали, відповідні t -му такту при t = 0, 1, 2..., через z(t), x(t), у(t). Прицьому, по умові, z(0)= z _o, а z(t) є Z, x(t) є X, у(t) є Y.

Абстрактний кінцевий автомат має один вхідний і один вихідний канали. У кожен момент t = 0, 1, 2... дискретного часу F-автомат знаходиться в певному стані z(t) з безлічі Z станів автомата, причому в початковий момент часу t=0 він завжди знаходиться в початковому стані z(0)=z_o. У момент t, будучи в стані z(t), автомат здатний сприйняти на вхідному каналі сигнал x(t) є X і видати на вихідному каналі сигнал y(t) = ψ [z (t), x (t) ], переходячи в стан z (t +1) = φ [z (t), x (t)], z (t) є Z, у (t) є Y. Абстрактний кінцевий автомат реалізує деяке відображення множини слів вхідного алфавіту X на множину слів вихідного алфавіту Y. Іншими словами, якщо на вхід кінцевого автомата, встановленого в початковий стан z₀, подавати в деякій послідовності букви вхідного алфавіту х(0), х(1), х(2)..., тобто вхідне слово, то на виході автомата послідовно з'являтимуться букви вихідного алфавіту у(0), у(1), у(2)..., утворюючи вихідне слово.

Таким чином, робота кінцевого автомата відбувається по наступній схемі: у кожному t-м такті на вхід автомата, що знаходиться в стані z(t), подається деякий сигнал x(t), на який він реагує переходом в (t+1) -му такті в новий стан z(t+1) і видачею деякого вихідного сигналу. Сказане вище можна описати наступними рівняннями:

для F – автомата першого роду, званого також автоматом Мілі

(4.2)

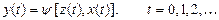(4.3)

для F – автомата другого роду:

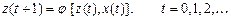(4.4)

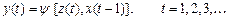(4.5)

Автомат другого роду, для якого

тобто функція виходів не залежить від вхідної змінної x(t), називається автоматом Мура.

По числу станів розрізняють кінцеві автомати з пам'яттю і без пам'яті. Автомати з пам'яттю мають більш за один стан, а автомати без пам'яті (комбінаційні або логічні схеми) володіють лише одним станом. Робота комбінаційної схеми полягає в тому, що вона ставить у відповідність кожному вхідному сигналу x(t) певний вихідний сигнал у(t), тобто реалізує логічну функцію вигляду

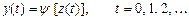
Ця функція називається булевою, якщо алфавіти X і У, яким належать значення сигналів х і у, складаються з двох букв.

Дата добавления: 2014-12-07