
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад 2. 5 страница
|
|
|
|
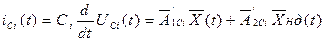
або
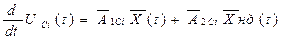
Склавши подібні рівняння для всіх індуктивних і ємкісних елементів в тій послідовності, в якій струми і напруга цих елементів представлені у векторі стану 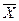 їх потім можна об'єднати в одне матричне рівняння:
їх потім можна об'єднати в одне матричне рівняння:
Дане рівняння носить назву рівняння стану. Значення матричних коефіцієнтів, які в нього входять, 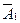 і
і 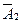 визначаються топологією ланцюга і параметрами елементів ланцюга.
визначаються топологією ланцюга і параметрами елементів ланцюга.
5.6.3 Рівняння виходу
Вихід аналізованого ланцюга позначимо через 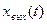 розуміючи під цим
розуміючи під цим 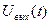 або
або 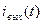 .
.
Вихід R – ланцюга лінійно пов'язаний з вектором стану 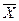 і вектором незалежних джерел
і вектором незалежних джерел 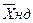 тобто
тобто
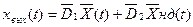
Це і є рівняння виходу. Тут 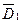 і
і 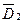 - матричні коефіцієнти, визначувані параметрами схеми.
- матричні коефіцієнти, визначувані параметрами схеми.
Слід відмітити, що схема зазвичай має один вихід, тому 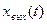 є скалярна, а не векторна величина.
є скалярна, а не векторна величина.
5.7 Матричні коефіцієнти математичної моделі електричноголанцюга
5.7.1 Матричні коефіцієнти рівняння струмів резистивних елементів
Користуючись правилом побудови топологічних рівнянь з використанням матриці головних перетинів 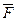
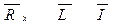
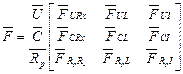 (5.3)
(5.3)
записуємо топологічні рівняння для струмів резистивних ребер і напруги резистивних хорд:
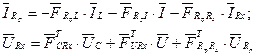 (5.4)
(5.4)
Топологічні рівняння (5.4) доповнимо компонентними рівняннями для резистивних елементів, що зв'язують напругу і струми цих елементів за законом Ома
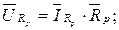
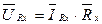 (5.5)
(5.5)
Тут 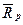 і
і 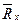 - матриці опорів резистивних ребер і резистивних хорд. У цих матрицях елементи, розташовані уздовж головної діагоналі, - опори відповідних резистивних елементів, решта елементів матриць має нульове значення.
- матриці опорів резистивних ребер і резистивних хорд. У цих матрицях елементи, розташовані уздовж головної діагоналі, - опори відповідних резистивних елементів, решта елементів матриць має нульове значення.
Виразимо в (5.4) напруги на резистивних елементах через струми цих елементів, використовуючи компонентні рівняння (5.5), після чого в (5.4) всі члени, що містять струми резистивних елементів, перенесемо в ліві частини рівності.
|
 (5.6)
(5.6)
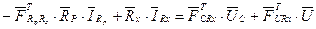 (5.7)
(5.7)
Об'єднаємо ці рівняння в одне матричне рівняння
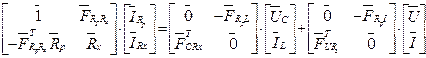
 |
Тут  - одинична матриця;
- одинична матриця;  - нульова матриця.
- нульова матриця.
З урахуванням введених позначень рівняння прийме вигляд
або
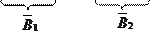
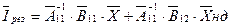
або
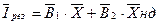
де 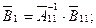
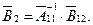
5.7.2 Матричні коефіцієнти рівняння стану
По матриці головних перетинів для довільної схеми
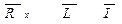
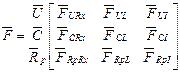
запишемо топологічні рівняння для 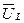 і
і 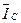 .
.
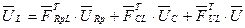 (5.8)
(5.8)
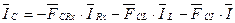 (5.9)
(5.9)
Компонентні рівняння для індуктивних і ємкісних елементів мають вигляд:
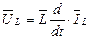 ;
; 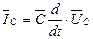 (5.10)
(5.10)
Підставимо в (5.8) і (5.9) вирази (5.10)
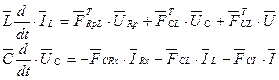 (5.11)
(5.11)
Далі виразимо 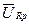 через
через 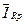 , використовуючи (5.5)
, використовуючи (5.5)
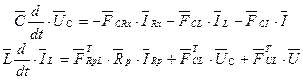 (5.12)
(5.12)
Об'єднаємо обидва рівняння в одне матричне. Отримаємо:
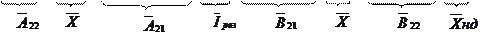
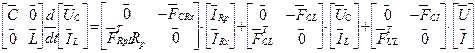
Тут 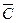 і
і 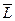 - матриці ємкостей і індуктивностей. У цих матрицях елементи розташовані уздовж головної діагоналі, решта елементів матриць має нульове значення.
- матриці ємкостей і індуктивностей. У цих матрицях елементи розташовані уздовж головної діагоналі, решта елементів матриць має нульове значення.
Таким чином
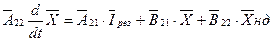 (5.13)
(5.13)
Раніше було виведено: 
Підставимо це рівняння в (5.13). Отримаємо
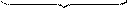
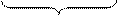
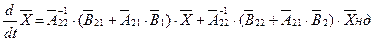
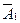
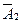
або 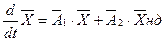
5.7.3 Матричні коефіцієнти рівняння виходу
Відгук Хвих на виході схеми може стати, як вже наголошувалося, напругою Uвих або струмом і вих. Якщо Хвих= Uвих, то його можна представити електричною сумою напруги гілок при обході деякого контура від однієї (початкової) вихідної клеми схеми до другої (кінцевої) клеми.
Якщо Хвих= і вих, то він може бути визначений алгебраїчним підсумовуванням струмів гілок, відповідних до вихідного ланцюга.
5.8 Математична модель електричного ланцюга з нелінійнимиелементами
Сформулюємо математичну модель електричного ланцюга, що має в своєму складі нелінійні резистори або нелінійні реактивні елементи – нелінійні конденсатори і нелінійні котушки індуктивностей.
5.8.1 Математична модель ланцюга з нелінійними резистивними елементами
Для виявлення загальної структури рівнянь математичної моделі ланцюга з нелінійними резистивними елементами скористаємося тим же прийомом, який був раніше використаний для отримання структури рівнянь лінійного ланцюга. Винесемо з аналізованої схеми незалежні джерела, реактивні елементи і нелінійні резистивні елементи.
При цьому частина схеми, що залишилася, є лінійною резистивною схемою. Далі проведемо еквівалентну заміну нелінійних резисторів джерелами напруги або струму. Підхід при цьому наступний:
а) якщо j -й нелінійний резистор заміщений джерелом напруги UH j, то струм цього джерела 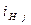 повинен виражатися через його напругу залежністю, відповідній вольт-амперній характеристиці j -го нелінійного резистивного елементу, тобто
повинен виражатися через його напругу залежністю, відповідній вольт-амперній характеристиці j -го нелінійного резистивного елементу, тобто 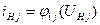 ;
;
б) якщо к -й нелінійний резистивний елемент заміщається джерелом струму 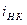 , то напруга на цьому джерелі повинна виражатися через струм джерела
, то напруга на цьому джерелі повинна виражатися через струм джерела 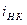 залежністю, що є вольт-амперною характеристикою к- гонелінійного резистивного элемента, тобто
залежністю, що є вольт-амперною характеристикою к- гонелінійного резистивного элемента, тобто 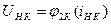 .
.
Представимо вектором 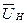 напруги джерел напруги, замінюючих групу нелінійних резистивних елементів, а вектором
напруги джерел напруги, замінюючих групу нелінійних резистивних елементів, а вектором 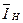 - струми джерел струму, що заміщають ці елементи. Ці вектори, у свою чергу, об'єднаємо у вектор
- струми джерел струму, що заміщають ці елементи. Ці вектори, у свою чергу, об'єднаємо у вектор
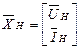
Таким чином, лінійна резистивна схема виявляється під впливом трьох груп джерел, напруги і струми яких представляються векторами 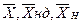 .
.
На підставі принципу лінійного зв'язку струмів в лінійній резистивній схемі з напругами і струмами джерел, що діють в схемі, можна структуру рівнянь математичній моделі ланцюга з нелінійними резистивними елементами представити в наступному вигляді:
а) рівняння струмів лінійних резистивних елементів
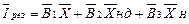 (5.14)
(5.14)
б) рівняння стану
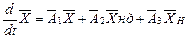 (5.15)
(5.15)
в) рівняння відгуку (виходу)
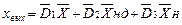 (5.16)
(5.16)
Як видно, особливість рівнянь математичної моделі ланцюга з нелінійними резистивними елементами, що відрізняє їх від рівнянь лінійного ланцюга, полягає в наявності в правій частині кожного з рівнянь третього члена, що містить вектор 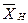 .
.
Система рівнянь (5.14) - (5.16) є неповною, оскільки число невідомих більше, ніж число рівнянь. Доповнимо цю систему рівнянням
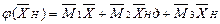 (5.17)
(5.17)
Воно відображає залежність струмів і напруг джерел що заміщають нелінійні резистивні елементів від напруги і струмів решти всіх джерел, що діють в схемі.
Система рівнянь (5.14) – (5.17) вже є повною. По рівняннях (5.15) і (5.17) знаходять спочатку вектори 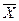 і
і 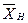 . Потім по значеннях цих векторів проводять обчислення по рівняннях (5.14) і (5.16).
. Потім по значеннях цих векторів проводять обчислення по рівняннях (5.14) і (5.16).
5.8.2 Математична модель ланцюга з нелінійними реактивними елементами
При розгляді ланцюгів, що містять нелінійні реактивні елементи, практичний інтерес представляє випадок, коли ємкість нелінійного ємкісного елементу є функцією напруги на цьому елементі
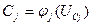 ,
,
а індуктивність нелінійного індуктивного елементу – функція струму в цьому елементі
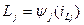
В цьому випадку значення нелінійних елементів залежать від вектора стану 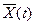 елементами якого є напруга на ємкісних елементах і струми в індуктивних елементах.
елементами якого є напруга на ємкісних елементах і струми в індуктивних елементах.
Структура рівняння стану ланцюга з нелінійними реактивними елементами може бути прийнята тією ж, що і структура рівняння стану ланцюга, що не містить нелінійних елементів, тобто
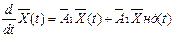 (5.18)
(5.18)
Проте матричні коефіцієнти 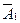 і
і 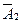 в цьому випадку є змінними, залежними від вектора стану
в цьому випадку є змінними, залежними від вектора стану 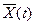 .
.
При інтегруванні рівняння (5.18) на кожному кроці інтеграції необхідно виконувати перерахунок коефіцієнтів 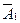 і
і 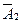 відповідно до нового стану вектора
відповідно до нового стану вектора 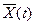 .
.
Матричні коефіцієнти  ,
, 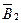 ,
, 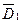 і
і 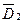 , що входять в рівняння
, що входять в рівняння
струмів резистивних елементів і рівнянь виходу не залежать від значень параметрів реактивних елементів.
5.9 Підготовка даних по електричній моделі для введення вЕОМ
Електричну модель аналізованої електронної схеми однозначно описує наступний набір даних:
а) топологічні дані (набір гілок і способи їх з'єднання);
б) компонентні дані (типи елементів в гілках і їх номінальні значення);
в) позитивні напрями струмів і напруги в гілках.
Щоб отримати топологічні дані, кожну гілку електричної моделі представляють у вигляді лінії, що сполучає відповідні вузли. Компонентні дані при цьому не враховуються. В результаті виходить так званий граф ланцюга.
Вузлом електричної моделі вважається всяке з'єднання двох і більше елементів, тобто кожен елемент має пару вузлів, між якими цей елемент включений.
Вузли на графі ланцюга нумеруються довільно.
При нумерації гілок графа необхідно дотримуватися наступної послідовності:
- спочатку нумеруються гілки з керованими джерелами напруги;
- потім йде нумерації гілок, що містять постійні джерела напруги;
- далі нумеруються гілки з ємкісними елементами;
- потім йде нумерація гілок з резистивними елементами;
- далі нумеруються гілки з індуктивними елементами;
- після цього йде нумерація гілок, що містять постійні джерела струму;
- закінчується нумерація гілок з керованими джерелами струму.
Нумерація гілок крізна, тобто пронумерувавши гілки однієї групи, переходять до нумерації гілок іншої групи, продовжуючи рахунок, поки не будуть пронумеровані всі гілки електричної моделі.
Позитивні напрями струму (напруга) в елементах моделі вибираються довільно. Вважається, що вибраний позитивний напрям для струму одночасно є і позитивним напрямом для напруги.
При підготовці компонентних даних може понадобитися масштабування параметрів елементів. Якщо цього не зробити, то при виконанні обчислень за допомогою ЕОМ можуть виникнути такі великі значення, які вийдуть за межі уявних в ЕОМ значень і приведуть до переповнювання розрядної сітки (великі значення, наприклад, можуть виникнути при багатократному множенні великих опорів 106·106·106) або можуть з'явитися дуже малі значення, що
розглядаються в ЕОМ як нуль (наприклад, при множенні малих ємкостей 10-12·10-12·10-12).
При масштабуванні для напруги, струмів, опорів, ємкостей, индуктивностей, частот і часу задаються відповідні масштабні коефіцієнти Mu, Mi, Mr, Mc, ML, Mf, Mt.
Якщо, наприклад, x – параметр якого-небудь елементу (наприклад, значення ємкості), а Mx – вибраний для нього масштабний коефіцієнт, то для ЕОМ цей параметр буде заданий значенням X:
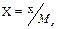
При виведенні цього параметра з ЕОМ виконується зворотне перетворення
x=Mx·X
Масштабні коефіцієнти повинні задовольняти очевидним співвідношенням
Mu=Mr·Mi; Mt=Mr·Mc; Mt=ML/Mr; Mf=1/Mt.
Звідси витікає, що з семи масштабних коефіцієнтів незалежно можуть бути вибрані лише три, чотири останніх знаходять за допомогою приведених виразів. Вибрати три незалежні масштабні коефіцієнти також потрібно правильно. Не можна вибирати як незалежні всі ті коефіцієнти, які входять в один вираз, який зв'язує ці коефіцієнти.
Зазвичай вибираються як незалежні Mu, Mr и Mc.
Масштабні коефіцієнти, значення яких задаються незалежно, доцільно вибирати такими, щоб в результаті масштабування набути значень параметрів Xі, найбільш близьких до одиниці. Крім того, самі масштабні коефіцієнти зручніше виражати числами, що є десять в якому-небудь цілому ступені.
При виборі значення масштабного коефіцієнта можна орієнтуватися на середнє геометричне найбільшого і найменшого значень параметрів елементів даного типу. Так, наприклад, при виборі Mс можна орієнтуватися на Cср, де
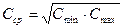
Тут Cmin и Cmax мінімальна і максимальна ємкості, що містяться в аналізованій схемі.
Дані, що вводяться в ЕОМ, повинні містити наступні відомості про кожну гілку схеми:
- вказівки про тип елементу гілки (U, C, R, L, I);
- порядковий номер гілки;
- номери вузлів, між якими розташована дана гілка;
- позитивний напрям гілки (він відображається тим, що на перше місце ставиться вузол, від якого гілка відходить і на друге місце – вузол, до якого гілка підходить);
- значення параметра елементу з урахуванням масштабування.
Повний набір даних по електричній моделі для введення в ЕОМ може бути представлений
таблицею 5.1
Таблиця 5.1
| Тип елемента | Номер гілки | Початковий вузол | Кінцевий вузол | Значення параметра |
Приклад
Дана електрична схема (рис.5.7). Вона ж є електричною моделлю. Необхідно підготувати дані про цю схему для введення в ЕОМ.
Граф даного ланцюга зображений на рис. 5.8. На графі показані вузли. Їх нумерація довільна (цифри в кружочках).
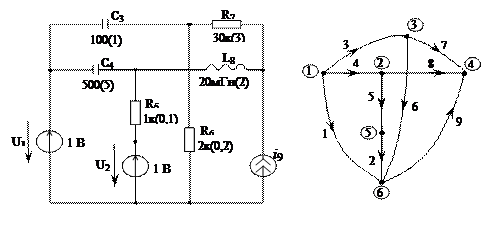
Рис.5.7 Схема електричого ланцюга Рис.5.8 Граф ланцюга
Пронумеруємо гілки графа відповідно до рекомендацій: постійні джерела напруги (їх два); ємкісні елементи (їх два); резистивні елементи (їх
три); індуктивні елементи (один); джерело струму (один).
Довільно указуємо на графі позитивний напрям струмів (напруг).
Приймемо незалежно вибираними масштабні коефіцієнти Mu, Mr, Mc.
Хай Mu=1. Для завдання Mr знайдемо середнє геометричне найбільшого і найменьшого значень резистивних елементів схеми і найближчий ступінь десяти приймемо в якості Mr:
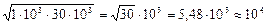 . Таким чином
. Таким чином 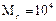 .
.
Аналогічно можна визначити масштабний коефіцієнт Mс:
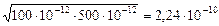 . Берем
. Берем  .
.
Решта масштабних коефіцієнтів обчислюється по виразах, які зв'язують масштабні коефіцієнти між собою
Mt=Mr·Mc=104·10-10=10-6;
Mf=1/Mt=106;
ML=Mt·Mr=10-6·104=10-2;
Mi=Mu/Mr=1/104=10-4.
На рис. 5.7 масштабовані значення елементів приведені в дужках.
Зведемо повний набір даних про електричну модель для введення в ЕОМ в таблицю
| Тип елементу | Номер гілки | Початковий вузол | Кінцевий вузол | Значення параметра |
| U | ||||
| U | ||||
| C | ||||
| C | ||||
| R | 0,1 | |||
| R | 0,2 | |||
| R | ||||
| L | ||||
| I |
6 Імовірнісне моделювання
6.1 Метод статистичних випробувань
Метод статистичних випробувань — це числовий метод математичного моделювання випадкових величин, який передбачає безпосереднє включення випадкового фактора в процес моделювання і є його істотним елементом. Вплив випадкових факторів на систему моделюється за допомогою випадкових чисел. Результатом моделювання є випадкові процеси або величини, які характеризують систему, що моделюється. Щоб їх імовірнісні характеристики (імовірність деяких подій, математичне сподівання, дисперсія випадкових величин, імовірності попадання випадкової величини в задану область та ін.) співпадали з аналогічними параметрами реальної системи або процесу під час моделювання потрібно отримати велику кількість реалізацій випадкових величин або процесів. Таким чином, метод полягає в багатократному проведенні випробувань побудованої ймовірнісної моделі і подальшій статистичній обробці результатів моделювання з метою визначення шуканих характеристик розглядуваного процесу у вигляді оцінок його параметрів. Точність оцінок цих параметрів визначає ступінь наближення розв'язку задачі до ймовірносних характеристик.
На практиці метод статистичних випробувань доцільно використовувати в таких випадках, коли:
♦ розв'язувати задачу цим методом простіше, ніж будь-яким іншим;
♦ досліджується система, функціонування якої визначається багатьма ймовірнісними параметрами елементарних явищ;
♦ важко або неможливо побудувати аналітичну ймовірнісну модель системи.
Важливою властивістю цього методу є те, що для звичайних числових методів обсяг обчислень зростає в разі збільшення розмірності задачі приблизно як показникова функція розмірності задачі, а для методу статистичних випробувань — лише як лінійна функція розмірності.
Незалежно від типу досліджуваної моделі системи, застосовуючи метод статистичних випробувань, необхідно виконати такі кроки.
1. Визначити, що являтиме собою кожне випробування і зазначити, яке випробування буде успішним, а яке — ні.
2. Обчислити кількість випробувань, які необхідно провести, щоб отримати результати із заданою точністю, і провести ці випробування.
3. Виконати статистичну обробку результатів випробувань та обчислити оцінки необхідних статистичних характеристик.
4. Проаналізувати точність отриманих статистичних характеристик.
Така послідовність кроків є обов'язковою під час розв'язування будь-якої задачі за допомогою методу статистичних випробувань. Однак конкретний зміст цих кроків залежить від поставленого завдання та типу досліджуваної системи. У цьому разі метод завжди потребує використання генераторів випадкових чисел із заданим законом розподілу.
У методі статистичних випробувань особливе значення відіграють випадкові числа, рівномірно розподілені в інтервалі [0,1]. Найважливіша їх властивість полягає в тому, що за їх допомогою можна отримати вибіркові значення, які мають будь-який інший розподіл, або промоделювати випадковий процес з різними статистичними властивостями.
Отже, для використання методу статистичних випробувань необхідні певні можливості, а саме:
♦ генерувати випадкові числа, рівномірно розподілені в інтервалі [0, 1];
♦ описувати модельовані випадкові явища функціями розподілу ймовірностей та ймовірнісними процесами;
♦ мати методи отримання випадкових величин функцій розподілу ймовірностей (дискретних і неперервних), які базуються на випадкових числах, рівномірно розподілених у інтервалі [0, 1];
♦ оцінювати статистичні характеристики випадкових величин з отриманих за допомогою методу статистичних випробувань чисел вибіркової послідовності;
Методи генерування випадкових чисел, рівномірно розподілених у інтервалі [0, 1], буде описано нижче.
За допомогою методу статистичних випробувань можна обчислити будь-які характеристики випадкових величин і процесів. Крім того, цей метод можна застосовувати для розв'язування не тільки ймовірнісних, а й детермінованих задач. Але під час його застосування слід пам'ятати, що для отримання результату з наперед заданою точністю необхідно провести велику кількість випробувань, для чого потрібні довгі послідовності випадкових чисел.
6.2 Генератори випадкових чисел
Найбільше прикладів генерування випадкових чисел можна знайти в ігровому бізнесі. Це номери в спортивних лотереях, числа, які випадають на рулетці, варіанти розкладу карт тощо. Більшість комп'ютерних ігор теж базується на випадкових числах.
6.2.1 Типи генераторів
Без комп'ютера використання випадкових чисел, передбачене методом статистичних випробувань, не має сенсу, тому генератори випадкових чисел повинні бути безпосередньо з'єднані з комп'ютером. Це можна зробити за допомогою апаратних приставок до комп'ютера (апаратні методи) або спеціальних програм (програмні методи). Крім того, під час моделювання можна використати готові таблиці випадкових чисел, які слід розміщати в пам'яті комп'ютера або на зовнішньому накопичувачі.
Апаратні методи генерування випадкових чисел базуються на використанні деяких фізичних явищ (наприклад, шумів електронних приладів, радіоактивного випромінення та ін.). Під час застосування апаратних генераторів випадковий електричний сигнал перетворюють у двійковий код, який уводиться в комп'ютер за допомогою спеціальних аналого-цифрових перетворювачів. Один з найбільш поширених методів — це використання шумів електронних приладів. Якщо на підсилювач не подавати ніякого сигналу та увімкнути його на повну потужність, то буде чутно шипіння (шум). Це і є шум електронних елементів підсилювача, який є випадковим процесом. Цей неперервний сигнал можна перетворити в дискретний. Існують різні схеми перетворення випадкового сигналу в послідовність двійкових цифр. У більшості випадків його підсилюють і встановлюють граничне значення напруги шумового сигналу, перевищення якого можна вважати значенням двійкової одиниці на деякому малому проміжку часу t. У протилежному випадку отримуємо двійковий нуль. Для отримання m - розрядного випадкового двійкового числа провадиться т вимірювань неперервного сигналу у фіксовані моменти часу t1, t2,..., tт-
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 390; Нарушение авторских прав?; Мы поможем в написании вашей работы!