Приклад 2. 4 страница

По характеру відліку дискретного часу кінцеві автомати діляться на синхронні і асинхронні. У синхронних F-aвmoматах моменти часу, в які автомат «прочитує» вхідні сигнали, визначаються примусово синхронізуючими сигналами. Після чергового синхронізуючого сигналу з урахуванням «считаного» і відповідно до рівнянь (4.2) — (4.5) відбувається перехід в новий стан і видача сигналу на виході, після чого автомат може сприймати наступне значення вхідного сигналу. Таким чином, реакція автомата на кожне значення вхідного сигналу закінчується за один такт, тривалість якого визначається інтервалом між сусідніми синхронізуючими сигналами. Асинхронний F-автомат прочитує вхідний сигнал безперервно, і тому, реагуючи на достатньо довгий вхідний сигнал постійної величини х, він може, як випливає з (4.2) — (4.5), кілька разів змінювати стан, видаючи відповідне число вихідних сигналів, поки не перейде в стійке, яке вже не може бути змінене даним вхідним сигналом.

Щоб задати кінцевий F-автомат, необхідно описати всі елементи множини F= (Z, X, Y,φ, ψ, z_o) тобто вхідний, внутрішній і вихідний алфавіти, а також функції переходів і виходів, причому серед множини станів необхідно виділити стан z_0, в якому автомат знаходився у момент часу t=0. Існуєдекілька способів завдання роботи F-автоматів, але найчастіше використовуються табличний, графічний і матричний.

Простий табличний спосіб завдання кінцевого автомата заснований на використанні таблиць переходів і виходів, рядки яких відповідають вхідним сигналам автомата, а стовпці - його станам.

При іншому способі завдання кінцевого автомата використовується поняття направленого графа. Граф автомата є набором вершин, відповідних різним станам автомата, і дуг графа, що сполучають вершини, відповідних тим або іншим переходам автомата.

При вирішенні завдань моделювання систем часто зручнішою формою є матричне завдання кінцевого автомата. При цьому матриця з'єднань автомата є квадратна матриця С=||сij||, рядки якої відповідають початковим станам, а стовпці — станам переходу.

Таким чином, поняття F-автомата в дискретно-детермінованому підході до дослідження на моделях властивостей об'єктів є математичною абстракцією, зручною для опису широкого класу процесів функціонування реальних об'єктів в автоматизованих системах обробки інформації і управління. Як такі об'єкти в першу чергу слід назвати елементи і вузли ЕОМ, пристрої контролю, регулювання і управління, системи часової і просторової комутації в техніці обміну інформацією і так далі. Для всіх перерахованих об'єктів характерна наявність дискретних станів і дискретний характер роботи в часі, тобто їх опис за допомогою F-схем єефективним. Але широта їх застосування не означає універсальності цих математичних схем. Наприклад, цей підхід непридатний для опису процесів ухвалення рішень, процесів в динамічних системах з наявністю перехідних процесів і стохастичних елементів.

4.4 Дискретно-стохастичні моделі ( P -схеми)

Розглянемо особливості побудови математичних схем при дискретно-стохастичному підході до формалізації процесу функціонування досліджуваної системи S. Оскільки суть дискретизації часу при цьому підході залишається аналогічною розглянутим в 4.3 кінцевим автоматам, той вплив чинника стохастичності прослідкуємо також на різновиді таких автоматів, а саме на імовірнісних (стохастическиих) автоматах.

У загальному вигляді імовірнісний автомат (англ. probabilistic automat) можна визначити як дискретний потактный перетворювач інформації з пам'яттю, функціонування якого в кожному такті залежить тільки від стану пам'яті в нім і може бути описане статистично.

Застосування схем імовірнісних автоматів (Р-схем) має важливе значення для розробки методів проектування дискретних систем, що проявляють статистично закономірну випадкову поведінку, для з'ясування алгоритмічних можливостей таких систем в обгрунтування меж доцільності їх використання, а також для вирішення завдань синтезу по вибраному критерію дискретних стохастичних систем, які задовольняють заданим обмеженням.

Введемо математичне поняття Р-автомата, використовуючи поняття, введені для F-автомата. Розглянемо множину G, елементами якої є всілякі пари (х_i, z_s), де х_i і z_s - елементи вхідної підмножини X і підмножини станів Z відповідно. Якщо існують дві такі функції φі ψ, і з їх допомогою здійснюються відображення G → Z і G → Y, то говорять, що F= (Z, X, Y,φ, ψ) визначає автомат детермінованого типу.

Введемо в розгляд більш загальну математичну схему. Хай Ф - множина всіляких пар виду (z_k, у_j), де у_j - елемент вихідної підмножини Y. Зажадаємо, щоб будь-який елемент множини G індукував на множині Ф деякий закон розподілу наступного вигляду:

Елементи з Ф …(z₁ y₁) … (z₁ y₂) … … (z_K y_J-1)(z_K y_J)
(х_i z_s) … b₁₁ b ₁₂ … b_K(J-1) b_kJ.

При цьому 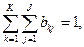де b_kj — вірогідність переходу автомата в стан z_k і появи на виході сигналу у_j якщо він був в змозі z_s, і на його вхід у цей момент часу поступив сигнал x_i. Число таких розподілів, представлених у вигляді таблиць, рівне числу елементів множини G. Позначимо множину цих таблиць через В. Тоді четвірка елементів P=(Z, X, Y, В) називається імовірнісним автоматом (Р-автоматом).

Хай елементи множини G індукують деякі закони розподілу на підмножинах Y і Z, що можна представити відповідно у вигляді:

Елементи з У … y₁ … y₂ … y _{J - 1} … y _J

(x_i, z_s) … q₁ … q₂ … q _{J - 1} … q _J

Елементи з Z … z₁ … z₂ … z _{k - 1} … z _k

(x_i, z_s) … z₁ … z₂ … z _{k - 1} … z _k

При цьому 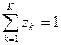і 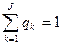де z_k і q_k — вірогідність переходу Р- автомата в стан z_k і появи вихідного сигналу у_к за умови, що Р-автомат знаходився в стані z_s і на його вхід поступив вхідний сигнал x_i.

Якщо для всіх k і j має місце співвідношення q_k z_i = b_kj, то такий Р-автомат називається імовірнісним автоматом Мілі. Ця вимога означає виконання умови незалежності розподілів для нового стану Р-автомата і його вихідного сигналу.

Хай тепер визначення вихідного сигналу Р-автомата залежить лише від того стану, в якому знаходиться автомат в даному такті роботи. Іншими словами, хай кожен елемент вихідної підмножини Y індикує розподіл вірогідності виходів, що має наступний вигляд:

Елементи з У … y₁ … y₂ … y_k-1 … y_k
(x_i, z_s) … s₁ … s₂ … s_I-1 … s_I

Тут де s_i — вірогідність появи вихідного сигналу y_s за умови, що Р-автомат знаходився в стані z_k.

Якщо для всіх k і i має місце співвідношення z_k s_i = b_ki, то такий Р-автомат називається імовірнісним автоматом Мура. Поняття Р-автоматів Мілі і Мура введене по аналогії з детермінованим F-автоматом, який задається F= (Z, X, Y, φ,ψ). Окремим випадком Р-автомата, що задається як Р= (Z. X, Y, В), є автомати, у яких або перехід в новий стан, або вихідний сигнал визначаються детерміновано. Якщо вихідний сигнал Р-автомата визначається детерміновано, то такий автомат називається Y-детерминированным імовірнісним автоматом. Аналогічно, Z-детерминированным імовірнісним автоматом називається Р-автомат, у якого вибір нового стану є детермінованим.

5 Математична модель електричного ланцюга

5.1 Компонентні і топологічні рівняння електричного ланцюга

Математична модель будь-якого електричного ланцюга складається з компонентних і топологічних рівнянь цього ланцюга.

5.1.1 Компонентні рівняння

Ці рівняння відображають залежність між струмом і напругою для елемента схеми:

а) для лінійного резистивного елементу:

U_R(t)=Ri_R(t);

б) для лінійного індуктивного елементу:

U_L(t)=L 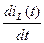; i_L(t)=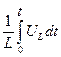

в) для лінійного ємкісного елементу:

i_c(t)=c 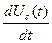; U_c(t)=

5.1.2 Топологичні рівняння

Ці рівняння характеризують спосіб з'єднання гілок, не відображаючи їх вмісту. Топологічні рівняння зазвичай будуються на законах Кирхгофа. Як відомо, є закон Кирхгофа для струмів (ЗКС) і закон Кирхгофа для напруг (ЗКН). ЗКТ формулюється так: алгебраїчна сума струмів пов'язаних з вузлом, рівна нулю. На рис 5.1a. показаний вузол. Для нього ЗКС записується так:

і₁ + i₂ - i₃ = 0; (5.1)

Струми, які втікають в вузол мають один знак (наприклад, знак «+»), а струми, які витікають з вузла – протилежний.

ЗКН звучить так: в замкнутому контурі алгебраїчна сума напруг на елементах контура рівна алгебраїчній сумі ЕРС, діючих в цьому контурі. Якщо в контурі вісутні ЕРС, то алгебраїчна суманапруг на елементах контура рівна нулю. Для контура, зображеного на рис 5.1б. ЗКС записують так:

U₁ + U₃ - U₂ = 0; (5.2)

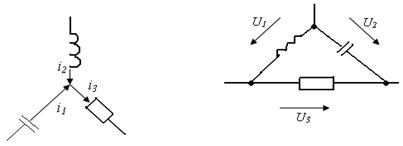
а) б)

Рис.5.1 Вузол і контур електричного ланцюга

Напруга, позитивний напрям якої співпадає з напрямом обходу контура, береться з одним знаком (наприклад, з знаком «+»), а напруга, позитивний напрям якої протилежний напряму обхода контура, - з протилежним знаком.

Рівняння (5.1) і (5.2) не містить відомостей про те, які типи елементів включені в гілці і які їх параметри. Відомо, що якщо в схемі n- вузлів, то по ЗКC можна скласти (n-1) незалежних рівнянь. Для складання рівнянь по ЗКН в схемі повинні бути знайдені незалежні замкнуті контури, тобто такі контура, в кожному з яких є хоч би одна гілка, що не входить у всі інші контури. Пошук незалежних контурів для ланцюга з складною конфігурацією (топологією) є відносно великою трудністю. Щоб отримати топологічні рівняння кожну гілку електричного ланцюга представляють лінією, яка сполучає відповідні вузли. Виходить так званий граф ланцюга.

Приклад:

Рис.5.2 Електричний ланцюг і його граф

Вибір позитивного напряму струму і напруги на графі робиться довільно. При цьому вважається, що выбраное позитивний напрям струму одночасно є і позитивним напрямом напруги.

5.2 Матриця головних перетинів і її властивості

Візьмемо граф деякого ланцюга (рис. 5.3а).

Рис.5.3 Граф електричного ланцюга і його дерева

Сукупність гілок графа, в якій опиняються представленими всі вузли, але при цьому не утворюється жодного замкнутого контура, називають деревом графа. На рис 5.3б,в представлено два варіанти дерев графа, побудовані з графа ланцюга (можна побудувати і інші варіанти дерева). Гілки, що входять у вибране дерево називаються ребрами. Гілки, що не увійшли до вибраного дерева, називаються хордами. Таким чином, кожна гілка графа є або його ребром, або хордою.

Замкнута лінія, яка одноразово перетинає гілки деякої сукупності гілок графа і розділяє граф на дві незв'язані частини називається перетином. Якщо така лінія перетинає одне ребро, то перетин вважається головним. На рис. 5.4 показаний приклад побудови головних перетинів. Тут головним перетинам привласнена нумерація тих ребер, які входять в ці перетини.

Зазвичай ЗКС формулюється щодо вузлів, але його можна формулювати і щодо головних перетинів. ЗКС для перетинів звучить так: алгебраїчна сума струмів щодо головного перетину рівна нулю.

Дотримуючись такого формулювання ЗКС, отримуємо наступну систему рівнянь для головних перетинів, показаних на рис. 5.4.

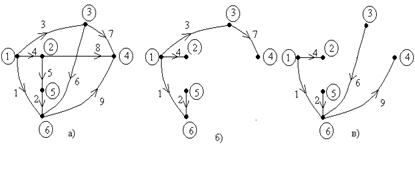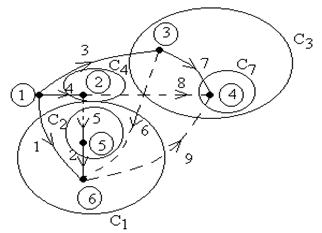
Рис.5.4 Приклад побудови головних перетинів

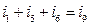або

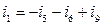(для головного перетину С₁);

(для головного перетину С₂);

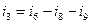(для главного сечения С₃);

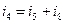(для головного перетину С₄);

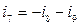(для головного перетину С₇).

Запишемо цю систему рівнянь в матричній формі:

Ввівши позначення для вхідних у вираз матриць, можна подібну систему рівнянь представити в загальному вигляді, справедливому для довільної схеми:

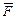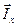Матриця називається матрицею головних перетинів. Вона визначає зв'язок між струмами ребер і струмами хорд . Рядки матриці головних перетинів належать ребрам, а стовпці - хордам графа.

З матриці витікає не тільки система рівнянь по ЗКС, але і система рівнянь по ЗКН. Елементи стовпців матриці є коефіцієнтами, що лінійно зв'язують напругу хорд, відповідних стовпцям, з напругою ребер. Так, для вказаної вище матриці можна записати наступну систему рівнянь для ЗКН:

У матричній формі цю систему рівнянь можна записати так:

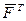де - вектор напруги хорд; - транспонована матриця ;

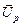- вектор напруги ребер.

Таким чином, матриця головних перетинів визначає повну систему топологічних рівнянь.

5.3 Матриця головних перетинів довільної схеми

У матриці головних перетинів, як вже наголошувалося, стовпці належать хордам, а рядки – ребрам дерева графа. При побудові дерева графа зазвичай в ребрах групують:

- джерела напруги;

- конденсатори;

- резистори.

У хордах, як правило, залишаються:

- резистори;

- індуктивності;

- джерела струмів.

Візьмемо узагальнену матрицю головних перетинів і виділимо в ній стовпці і рядки, що належать конкретним елементам.

Тут 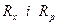- резистори, включені відповідно в хорди і ребра.

Враховуючи таке позначення, можна матрицю розбити на підматриці.

Індекси підматриць указують типи гілок, яким належать рядки і стовпці підматриці.

Сформоване вище правило побудови рівнянь струмів і напруги з використанням матриці 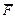можна розповсюдити і на випадок, коли ця матриця представлена підматрицями.

Підматриці, розташовані в рядку і узяті із зворотним знаком, є коефіцієнтами, що зв'язують вектор струму групи ребер, якій належить рядок, з вектором струму відповідних груп хорд. Наприклад:

Підматриці, розташовані уздовж стовпця деякої групи однотипних хорд, після транспортування є коефіцієнтами, що лінійно зв'язують вектор напруги цих хорд з вектором напруги відповідних груп ребер. Наприклад:

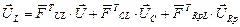
5.4 Формування матриці головних перетинів

Формування матриці 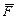проводиться в два етапи. На першому етапі по введених в ЕОМ даним ланцюга формується структурна матриця (матриця інциденцій). На другому етапі шляхом перетворення із структурної матриці будують матрицю .

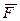5.4.1 Формування структурної матриці

Розглянемо побудову матриці на прикладі графа ланцюга, представленого на рис.5.3а. Складемо матрицю наступного вигляду. Припишемо стовпці матриці певним гілкам графа, а рядки – його вузлам. Дамо елементам 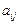цієї матриці наступні значення:

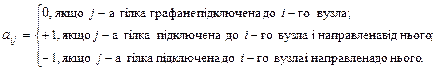
При нумерації гілок дотримуються наступної ієрархії: керовані джерела напруги, незалежні джерела напруги, ємкісні, резистивні, індуктивні елементи, незалежні джерела струму, керовані джерела струму.

Нумерація починається з гілок, що належать вищому ступеню ієрархії. Вичерпавши їх продовжать нумерацію, перейшовши до гілок наступного ступеня ієрархи і так далі, поки не буде пронумеровані всі гілки схеми. Саме так були пронумеровані гілки в графі на рис.5.3а. Для цього графа побудуємо наступну матрицю:

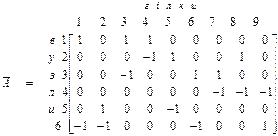
Кожен i - й рядок такої матриці показує, які гілки підключені до i - го вузла і який їх напрям щодо вузла; а кожен j - й стовпець указує, з якими вузлами сполучена j - а гілка.

Слід зазначити, що один з рядків матриці не є незалежним, він не несе інформації і може бути без наслідків вилучений з матриці. Викресливши в 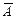останній рядок, отримуємо:

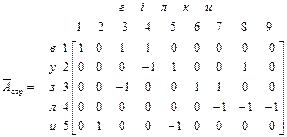
Цю матрицю називають структурною і вона дає топологічний опис ланцюга. Оскільки рядки матриці указують гілки, підключені до відповідних вузлів, і їх напрям щодо вузлів, то перемножаючи рядки матриці на вектор струмів гілок , отримуємо алгебраїчну суму струмів у вузлах, рівну нулю (відповідно до ЗКC). Отже

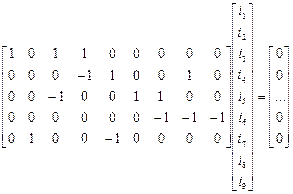
Цей матричний запис відповідає наступній системі рівнянь:

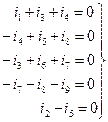
5.4.2. Отримання матриці головних перетинів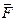

Для отримання матриці 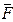необхідно дану систему рівнянь вирішити щодо струмів ребер. Цю операцію можна виконати методом виключення змінних: зі всіх рівнянь, окрім першого, виключається струм i_{1 ,} потім зі всіх рівнянь, окрім другого виключаємо струм i₂, і так далі Виключення змінних дозволяє перетворити матрицю 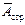так, що в її лівій частині утворюється одинична матриця, а права частина буде шуканою матрицею головних перетинів 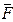. В ході перетворення використовується перестановка рядків і стовпців матриці, підсумовування або віднімання рядків. Покажемо це на прикладі перетворення матриці

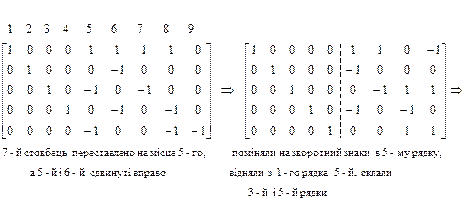
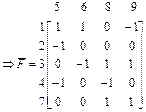
Така сама матриця була отримана раніше.

5.5 Вектор стану електричного ланцюга

Візьмемо лінійний RLC – ланцюг. Винесемо за межі аналізованого лінійного RLC – ланцюга (рис. 5.5а) незалежні джерела і реактивніелементи L і C.

Рис.5.5 Лінійий електричний ланцюг

До числа незалежних джерел входять джерела живлення і джерела вхідних сигналів. При цьому вважаємо, що аналізована схема не містить керованих джерел і не містить особливостей. Під особливостями зазвичай розуміють замкнуті контури, складені:

а) тільки з джерел напруги (U- контури);

б) тільки з ємкісних елементів (C - контури);

в) з джерел напруги і ємкісних елементів (UC - контури);

або гілки, що містять:

а) тільки джерела струму (J - перетини);

б) тільки індуктивні елементи (L - перетини);

в) джерела струму і індуктивні елементи (JL - перетини).

Частина схеми, що залишилася, після винесення з неї вказаних елементів буде лінійним пасивним R - ланцюгом (рис 5.5.б).

Струми (напруги) в елементах R – ланцюга не змінюються, якщо індуктивні елементи замінити джерелами струму , а ємкісні елементи – джерелами напруги (рис. 5.6).

При цьому джерела, що заміщають реактивні елементи, повинні бути такими, щоб їх струми і напруги в кожен момент часу мали ті ж значення, що і струми і напруги відповідних елементів.

Рис.5.6 Пасивний резистивний ланцюг

Пасивний лінійний R - ланцюг, представлений на рис.5.6, знаходиться під впливом джерел двох типів:

а) незалежних джерел живлення і джерел вхідних дій, представлених вектором:

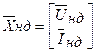
б) джерел заміщення реактивних елементів, представлених вектором:

Останній вектор називається вектором стану.

Напруги і струми незалежних джерел вважаються відомими. Тому напруги і струми елементів RLC - ланцюгa у будь-який момент часу визначаються вектором стану для цього моменту часу.

Метод аналізу схеми, заснований на використанні вектора стану, як незалежна змінна, називається методом змінних стану.

5.6 Математична модель лінійного електричного ланцюга

Математична модель лінійного електричного ланцюга включає:

- рівняння струмів резистивних елементів;

- рівняння стану;

- рівняння виходу.

Розглянемо загальну структуру цих рівнянь.

5.6.1 Рівняння струмів резистивних елементів

Ха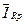й и - вектори струмів, які включають струми резистивних ребер і струми резистивних хорд. Введемо вектор струмів резистивних елементів

Очевидно

,

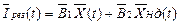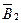де и - матричні коефіцієнти, значення яких визначається топологією ланцюга і значеннями резистивних елементів ланцюга.

Отримане вище рівняння і є рівнянням струмів резистивних елементів.

5.6.2 Рівняння стану

Напруга на індуктивному елементі 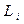, как відомо, пов'язана із струмом в цьому елементі співвідношенням

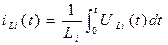
Ця напруга діє між відповідними вузлами R - ланцюга, до яких підключений елемент 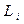. Очевидно, ця напруга зв'язана лінійною залежністю з векторами 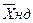і .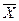

або

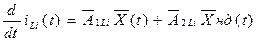
Струм ємкісного елементу як відомо, пов'язаний з напругою на цьому елементі співвідношенням

,

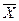Цей струм належить R – ланцюгу, витікаючи з вузла і втікаючи у вузол, між якими включений ємкісною елемент . Отже, струм може бути зв'язаний лінійною залежністю з векторами і .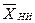

Дата добавления: 2014-12-07