Рішення. Розділ 1.4. Знаходження ймовірності появи події з застосуванням елементів комбінаторики

Розділ 1.4. Знаходження ймовірності появи події з застосуванням елементів комбінаторики

Рішення

За формулою (1.4)

Задача:

Нехай маємо множину із п елементів, які мають властивість рівноможливості випадкового вибору кожного з них. Нехай серед цих заданих п елементів маємо т (т п), які мають задану ознаку (наприклад, номер, колір, якість, тощо). Випадково здійснюється вибір k елементів (k п). Знайти ймовірність того, що серед обраних k елементів буде l елементів (l ) і які мають задану ознаку. Тоді ймовірність цієї події визначається за формулою:

(1.5)

Наприклад:

В партії з 10 деталей знаходиться 7 стандартних. Знайти ймовірність того, що серед 6 взятих навмання деталей 4 стандартні.

Подія А – серед 6 взятих деталей 4 стандартні.

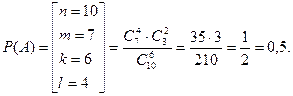
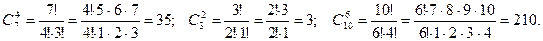
Задачі до розділу 1.4

Задача 1.4.1

У відділі працює 6 чоловіків і 4 жінки, за табельними номерами навмання відібрано 7 людей. Знайти ймовірність того, що серед відібраних будуть 3 жінки.

Рішення

Загальне число можливих елементарних результатів випробувань дорівнює числу способів, якими можна з загальної кількості чоловік (10) обрати 7, тобто - кількості сполучень з 7 по 10. Підрахуємо число результатів, що сприятимуть події „серед обраних три жінки”: обрати 3 жінки з 4 можна способами, при цьому ті, що лишилися 10 – 4 = 6, повинні бути чоловіками, з яких буде обрано 7 – 3 = 4, яких можна обрати 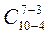= 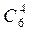способами. Відповідно число сприятливих випадків дорівнює .

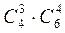Шукана ймовірність дорівнює відношенню кількості сприятливих випадків до загальної кількості випадків:

.

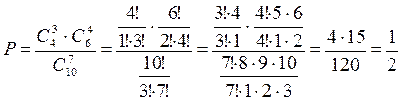Задача 1.4.2

В ящику 5 стандартних і 3 браковані деталі. Навмання витягли 4 деталі. Знайти ймовірність того, що серед них буде 3 стандартні і 1 бракована деталь.

Рішення

Подія А – серед чотирьох вилучених деталей три стандартні і одна бракована.

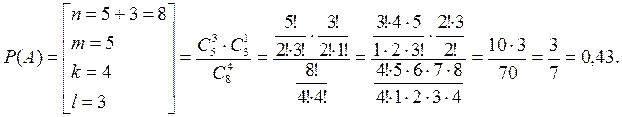
Задача 1.4.3

В коробці 15 калькуляторів, серед яких 10 інженерних. Службовець навмання обирає 3 калькулятора. Знайти ймовірність того, що обрані калькулятори будуть інженерними.

Задача 1.4.4

В групі 11 студентів, серед яких 6 навчаються на „відмінно” і „добре”. За списком обрано 8 студентів. Знайти ймовірність того, що серед обраних студентів 5 навчаються на „відмінно” і „добре”.

Задача 1.4.5

В партії з 50 деталей, 47 стандартних. Навмання обрано 43 деталі. Знайти ймовірність того, що серед обраних деталей 45 стандартних.

Дата добавления: 2014-12-07