Розв’язання. 1. Ідентифікуємо змінні моделі:

1. Ідентифікуємо змінні моделі:

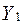— рівноважна кількість споживання продукту, ендогенна змінна;

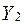— ціна за одиницю продукції, ендогенна змінна;

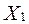–– дохід на душу населення, екзогенна змінна;

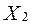–– витрати на виробництво одиниці продукції, екзогенна змінна.

Функція попиту: .

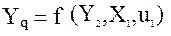Функція пропозиції: .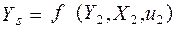

Умова ринкової рівноваги: .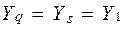

2. Специфікуємо модель на основі системи одночасових структурних рівнянь:

;

;

.

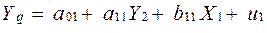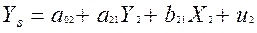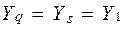Цю систему одночасових структурних рівнянь можна переписати у вигляді:

;

.

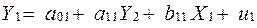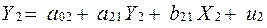3. Розглянемо умови ідентифікованості кожного рівняння моделі:

3.1. ;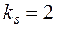

;

;

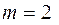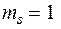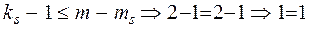, звідси перше рівняння системи є точноідентифікованим.

3.2. ;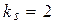

;

;

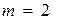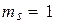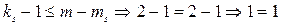, звідси друге рівняння системи є також точно ідентифікованим.

Оскільки обидва рівняння системи є точно ідентифікованими, то оцінку параметрів моделі можна виконати непрямим методом найменших квадратів.

4. Оцінимо параметри моделі НМНК.

4.1. Перейдемо від структурної до приведеної форми рівнянь. Для цього в другому рівнянні замість 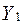підставимо вираз у правій частині першого рівняння.

Запишемо:

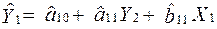(1); (1)

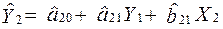(2). (2)

Підставимо значення 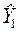у друге рівняння, звідси:

;

;

;

.

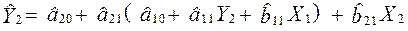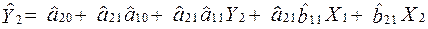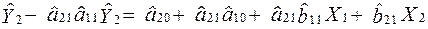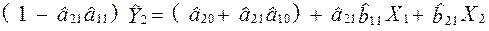Розділимо обидві частини рівняння на 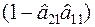та отримаємо:

.

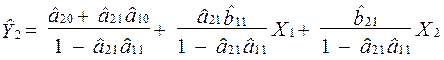Замінимо

;

;

.

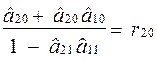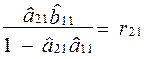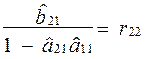У результаті отримаємо друге рівняння моделі в приведеній формі:

.

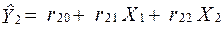А тепер значення структурного рівняння 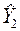(2) підставимо в перше рівняння моделі (1) і наведемо його у приведеній форми.

;

.

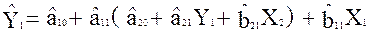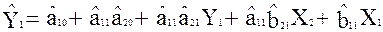Перенесемо 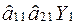в ліву частину рівняння:

.

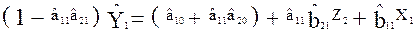Розділимо обидві частини рівняння на 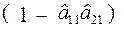і отримаємо:

.

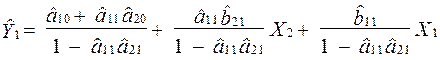Замінимо:

;

;

.

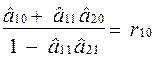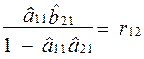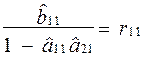У результаті отримаємо перше рівняння моделі в приведеній формі:

.

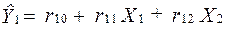Таким чином, економетрична модель у приведеній формі:

;

.

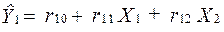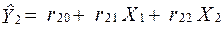Оцінимо параметри кожного рівняння цієї моделі за методом 1МНК:

.

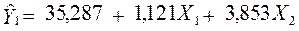Стандартні помилки:

;

.

.

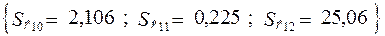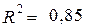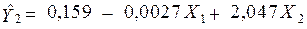Стандартні помилки:

;

.

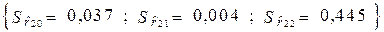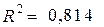Перейдемо від приведеної форми до структурної. Для цього розв’яжемо систему рівнянь:

,

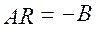де

;

;

.

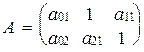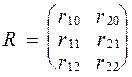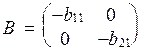Звідси:

;

.

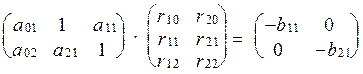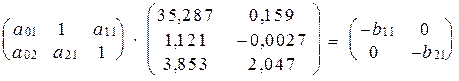Перемноживши матриці, одержимо систему рівнянь:

.

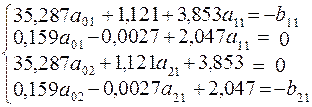Ця система містить шість невідомих параметрів. Виразивши два з них через два інші (друге та третє рівняння) перейдемо до системи чотирьох лінійних рівнянь з чотирма невідомими. Розв’язавши її, знайдемо невідомі параметри економетричної моделі в структурній формі.

Отримати економетричні рівняння в структурній формі можна також виключивши змінну 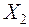з першого рівняння в приведеній формі та 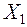з другого.

Визначимо 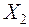з другого рівняння приведеної форми моделі:

;

;

.

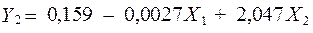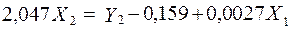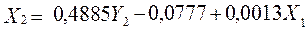Підставимо це значення в перше рівняння приведеної форми моделі:

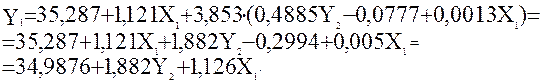
Звідси: .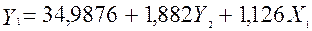

Визначимо 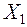з першого рівняння приведеної форми моделі:

;

;

.

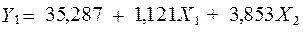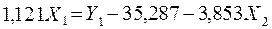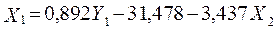Підставимо це значення в друге рівняння приведеної форми моделі:

;

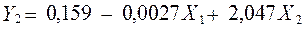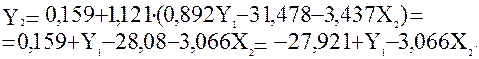
Звідси .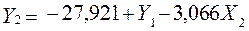

Таким чином, економетрична модель у структурній формі запишеться так:

;

.

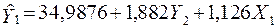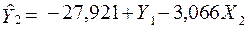Визначимо коефіцієнти еластичності:

;

;

.

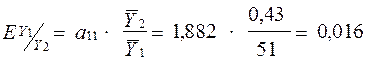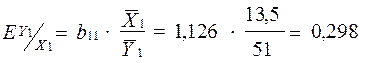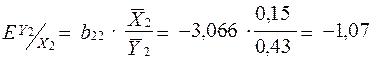На основі коефіцієнтів еластичності можна зробити висновок, що при зростанні ціни на 1 % рівноважна кількість споживання продукту збільшиться на 0,016 %. При збільшенні доходу на 1 % рівноважна кількість споживання збільшиться на 0,298 %. Зростання затрат на виробництво на 1% сприятиме зниженню ціни на 1,07%.

Серед цих співвідношень лише друге, яке характеризує зв’язок між доходом і кількістю споживання, може відповідати реальним умовам. Перше та третє співвідношення не відповідають теоретичним уявленням про цей зв’язок. На практиці, як правило, він має протилежний напрямок. Зростання цін може знижувати споживання, а збільшення затрат на виробництво буде сприяти зростанню цін, а не навпаки. Але тут треба мати на увазі, що дані розглянутого прикладу є умовними, які використані для відпрацювання методики використання НМНК.

Дата добавления: 2014-12-07