Тема 10. Економетричне моделювання на основі виробничої функції Кобба-Дугласа

1.Виробнича функція – це економетрична модель, яка кількісно описує зв’язок основних результативних показників виробничо-гос­подарської діяльності з факторами, що визначають ці показники. До основних показників належать дохід, прибуток, рентабельність, продуктивність праці, собівартість тощо.

Перше поняття виробничої функції пов’язане з математичним моделюванням технологічної залежності між обсягом продукції, що випускається, і кількісними характеристиками витрат ресурсів. Звідси і назва функції «виробнича». Уперше така функція була побудована американськими дослідниками Коббом і Дугласом ще в 30-ті роки ХХ ст. за даними про функціонування обробної промисловості США протягом двадцяти років і є класичним прикладом економетричного моделювання.

Функція Кобба–Дугласа (CDPF) належить до найвідоміших виробничих функцій, що набули широкого застосування в економічних дослідженнях, особливо на макрорівні. Класична виробнича функція Кобба–Дугласа має вигляд:

Y = aF ^a L ^{1 – a},(1)

де Y – обсяг продукції; F – основний капітал; L – робоча сила.

Сума параметрів або степінь однорідності класичної функції Коб­ба–Дугласа дорівнює одиниці. А це означає, що при збільшенні обох виробничих ресурсів на одиницю обсяг продукції також збільшиться на одиницю. Отже, ефективність ресурсів у такому разі стала.

2.Практичні дослідження функції Кобба–Дугласа показали, що припущення про лінійну однорідність на практиці виконується рідко. Тому була запропонована виробнича функція загальнішого вигляду:

Y = aF ^a L ^b. (2)

Сума параметрів (a + b) на відміну від попереднього випадку може бути як меншою, так і більшою від одиниці. Якщо (a + b) > 1, то темпи росту обсягу продукції вищі за темпи росту виробничих ресурсів, а якщо (a + b) < 1, то, навпаки, темпи росту продукції нижчі за темпи росту ресурсів.

Припустимо, що рівень кожного виробничого ресурсу збільшився на r %, тоді величини їх відповідно дорівнюватимуть і .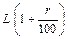

Обсяг продукції на основі виробничої функції запишеться так:

Звідси при a + b > 1 обсяг продукції зростає більш ніж на r %; при a + b < 1 – менш ніж на r %; при a + b = 1 продукція збільшиться на r %. Узявши частинні похідні від виробничої функції Кобба–Дугласа, одержимо:

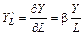; (3).

Це означає, що граничний приріст продукції за рахунок приросту кожного ресурсу визначається як добуток коефіцієнта еластичності на середню ефективність ресурсу. Параметр a у функції Кобба–
Дугласа залежить від вибраних одиниць вимірювання Y, F, L; водночас числове значення цього параметра визначається також ефективністю виробничого процесу. У цьому можна переконатись, порівняв­ши дві виробничі функції, які відрізняються одна від одної лише значенням параметра a.

Для фіксованих значень F і L тій функції, в якої більше числове значення параметра a, відповідає більше значення Y. Отже, і виробничий процес, який описується цією функцією, буде ефективнішим. Другі похідні функції Кобба–Дугласа мають такий вигляд:

; (4).

Беручи до уваги, що 0 < a < 1 і 0 < b < 1, Y_FF < 0 і Y_LL < 0, то справедливий висновок: при збільшенні ресурсів граничний приріст обсягу продукції зменшуватиметься. Якщо обсяг продукції у функції Кобба–Дугласа вважати сталим (const), то можна обчислити граничні норми заміщення ресурсів:

(5).

Звідси бачимо, що гранична норма заміщення ресурсів у функції
Кобба–Дугласа визначається як добуток співвідношень величин ресурсів та їх коефіцієнтів еластичності.

Швидкість зміни норми заміщення ресурсів у зв’язку зі зміною величини ресурсів обчислюється так:

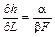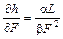; (6).

Мірою швидкості зміни h є еластичність заміщення ресурсів F і L, що визначається як відношення зміни величини ресурсів до зміни величини h:

(7).

Отже, еластичність заміщення в кожній точці кривої, що характеризує виробничу функцію Кобба–Дугласа, дорівнює одиниці.

Розглянемо тепер поводження функції при зміні масштабу виробництва. Для цього припустимо, що витрати кожного ресурсу виробництва збільшилися в l раз, тоді нове значення Y¢ визначатиметься так:

Y ¢ = a (l F)^a (l L) ^b = l^{a + b} Y (8).

Ступінь однорідності цієї функції дорівнює a + b. Якщо a + b = 1, то рівень ефективності ресурсів не залежить від масштабів виробництва. Якщо a + b < 1, то, як уже стверджувалось, з розширенням масштабів виробництва середні витрати ресурсів в розрахунку на одиницю продукції зменшуються, а при a + b > 1 – збільшуються. Причому ці властивості не залежать від числових значень F і L і зберігаються в кожній точці виробничої функції.

За припущення, що мета господарської діяльності – максимізація прибутку, можна проілюструвати інші властивості виробничої функції. Запишемо функцію прибутку:

П = bY ^{r + 1} – wL – rF + l[ f (F, L) – Y ].

Підприємець вибирає такі значення Y, L, F, які максимізують прибуток при обмеженнях, що накладаються виробничою функцією. Величини b, w, r – параметри функції прибутку, l – множник Лагранжа. Якщо виробничий процес у даному співвідношенні опису-
ється функцією Кобба–Дугласа, то можна записати умови максимізації прибутку:

; ; ,

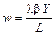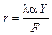l = (r + 1) P при r ¹ – 1, де P = bY ^r.

Звідси обсяги ресурсів такі:

; .

У такому випадку максимальне значення випуску продукції, якщо a + b ¹ 1, можна записати так:

.

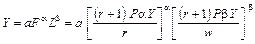При r = 1згідно із записаними щойно умовами максимізації
одержимо:

; .

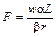Отже, необхідні умови для забезпечення максимізації прибутку дають змогу визначити відповідні витрати робочої сили і основного капіталу. З розширенням масштабів виробництва ефективність витрат ресурсів падає, що відповідає максимізації прибутку в умовах досконалої конкуренції.

3.Найпридатнішими для побудови економетричної моделі продуктивності праці є такі аналітичні форми функцій:

· лінійна;

· степенева.

Запишемо загальний вигляд цих функцій:

лінійна – 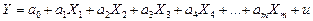; (9)

степенева – 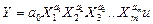, (10)

де Y – продуктивність праці, залежна змінна;

– чинники економічної діяльності, що впли­вають на продуктивність праці (незалежні або пояснювальні змінні);

u – стохастична складова, яка акумулює в собі вплив усіх випадкових чинників;

– параметри моделі продуктивності праці.

Лінійна форма моделі продуктивності праці відтворює адитив­ний закон формування продуктивності праці (рівень продуктивності праці є сума часток, що їх вносить у загальний рівень кожний чинник).

Степенева форма відтворює мультиплікативний закон формування продуктивності праці (рівень продуктивності праці є добуток часток, що їх вносить у загальний рівень кожний чинник).

Як було зазначено раніше, що узявши логарифми (натуральні або десяткові) лівої та правої частин виразу (4), можна перейти від степеневої до лінійно-логарифмічної моделі продуктивності праці:

,

тобто степенева функція реалізується як лінійна, якщо вихідні дані для побудови моделі брати не в абсолютних одиницях їх виміру, а в логарифмах.

3.Побудувати модель продуктивності праці – це означає оцінити параметри моделі .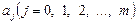

1. Побудувати модель продуктивності праці, що характеризує залежність між продуктивністю праці та основними чинниками, які впливають на неї.

2. Оцінити статистичну значущість моделі та оцінок її параметрів і зробити висновки.

3. Обчислити всі економічні характеристики взаємозв’язку і зробити економічний аналіз.

4. Виконати прогноз продуктивності праці на наступні чотири місяці, якщо задані очікувані значення чинників, що впливають на неї.

Вихідні дані наведені в табл. 10.1.

Дата добавления: 2014-12-07