Пример дискретного вариационного ряда

xi	1,5	3,5	5,5	7,5	9,5
ni	4	10	3	2	1
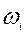
	0,2	0,5	0,15	0,1	0,05

Строим соответствующий полигон частот.

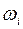
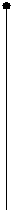
0.5

0.3

0.2

0.1

1 2 3 4 5 6 7 8 9 10 X_i

Рисунок 1.Полигон частот

Полигон используется при графическом представлении дискретных вариационных рядов, когда число вариант невелико (n≤30).

Для графического представления интервального вариационного ряда служит гистограмма - ступенчатая фигура, которая состоит из прямоугольников, основаниями которых являются интервалы длиной 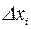, а высоты равны отношению 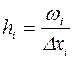(см. рис. 2). Площадь 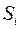i -го частичного прямоугольника численно равна относительной частоте попадания в интервал :

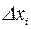(3)

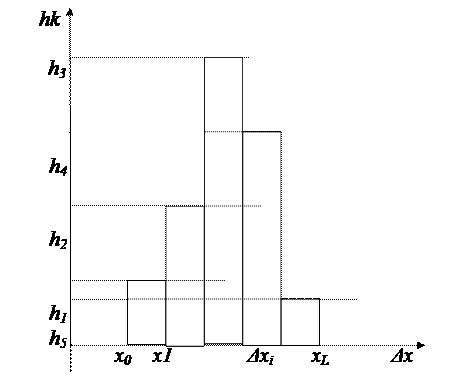
Рисунок 2.Гистограмма

Площадь всей гистограммы численно равна суме всех частот ряда, т.е. должна быть равна единице (исходя из условия нормировки):

где к =1,2,3,…, L.

Интервальный вариационный ряд можно преобразовать в дискретный.

Для этого надо вычислить в каждом интервале среднее значение 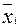и :

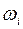; , (4)

где 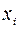- значения вариант, попавших в i -ый интервал, 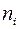- количество вариант, попавших в i -ый интервал.

Полигон и гистограмма являются приближенными оценками плотности распределения вероятностей.

Среднее арифметическое значений вариант характеризует приближенно математическое ожидание случайной величины, т.е. является его оценкой:

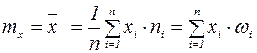(5)

Оценка дисперсии. Исправленная дисперсия характеризует рассеивание случайной величины и находится по формуле:

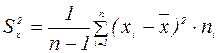(6)

или 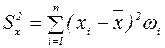для n >30 (7)

Дисперсия имеет размерность квадрата измеряемой величины. Чтобы характеризовать рассеивание в тех же единицах, что и измеряемая величина, вычисляют среднее квадратичное отклонение:

(8)

Все эти величины необходимо вычислить, т.е. определить характеристики экспериментального распределения заданных х _i, а также определить, отличается ли полученная эмпирически оценка плотности распределения от нормального закона.

Порядок расчета этих характеристик поясним на примере. По известным данным измерения роста 1000 взрослых мужчин оценим характеристики распределения и сравним его с нормальным.

В первой строке таблицы приводятся интервалы роста в сантиметрах, во второй – число мужчин, имеющих рост в пределах этого интервала.

Рост x (см)	143-152	152-161	161-170	170-179	179-188
Число ni мужчин

Таблица 2

Дата добавления: 2014-12-07