П Л А Н. 11. Дуденко Н.В., Павлоцька Л.Ф., Вялкіна С.П

Методичні матеріали

11. Дуденко Н.В., Павлоцька Л.Ф., Вялкіна С.П. – Практикум для проведення тестового контролю знань з дисципліни «Біохімія». – Х.: 2004. – 107 с.

1. Визначники 2-го та 3-го порядків.

2. Властивості визначників. Розклад визначників за елементами рядка (стовпця.

3. Визначники n-го порядку та їх обчислення.

1. Матриця розміром m x n –це сукупність чисел, розміщених у вигляді прямокутної таблиці, яка має m рядків та n стовпців.

Матриці позначають великими літерами латинського алфавіту та круглими дужками. Така матриця має вигляд:

А=

або А= 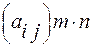, A=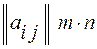

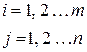
Кожен елемент матриці А має два індекси: перший вказує номер рядка, другий –номер стовпця

Якщо m=n, то матриця буде квадратною.

n –порядок матриці.

Визначник – це число, яке знаходиться з елементів квадратної матриці за певним правилом.

Якщо квадратна матриця позначена літерою , то її визначник позначається 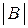або 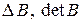. Друга назва – детермінант.

Визначники 2-го порядку:

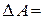
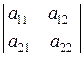
допоміжна головна

діагональ діагональ

(-) (+)

(дорівнює різниці добутків елементів головної та допоміжної діагоналей)

Приклад: =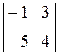

Визначники 3-го порядку:

а) Обчислення за правилом трикутників:

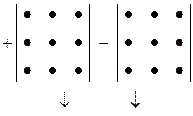
головна допоміжна

діагональ діагональ

(-) (+)

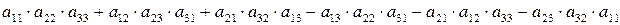
б) Обчислення за правилом Саріуса:

гол. діаг. допом. діаг.

Приклад:

2. Властивості визначників.

1) Визначник при транспонуванні не змінюється (при заміні рядків на стовпці).

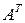- транспонована матриця

2) Якщо у визначнику поміняти місцями будь-які рядки (або стовпці), то визначник змінить знак на протилежний.

3) Якщо визначник має два однакових рядки (або стовпці), то він дорівнює нулю.

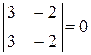
4) Якщо у визначнику усі елементи одного рядка (або стовпця) помножити на дійсне число k, то визначник зміниться також в k разів

Наслідок 1. Спільний множник усіх елементів будь-якого рядка (або стовпця)

визначника можна винести за знак визначника

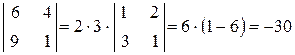
Наслідок 2. Якщо усі елементи будь-якого рядка (або стовпця) визначника

дорівнюють нулю, то визначник дорівнює нулю.

5) Визначник, у якого відповідні елементи двох будь-яких рядків (або стовпців) пропорційні, дорівнює нулю.

Доведення випливає з властивостей 3, 4

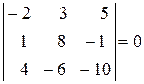
6) Якщо у визначнику елементи будь-якого рядка (або стовпця) є сумою двох доданків, то він дорівнює сумі двох відповідних визначників,

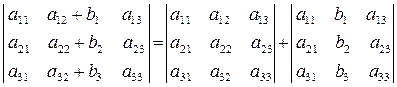
7) Якщо до всіх елементів будь-якого рядка (або стовпця) визначника додати відповідні елементи іншого рядка (або стовпця) цього визначника, помножені на одне й те ж саме число, то визначник не зміниться

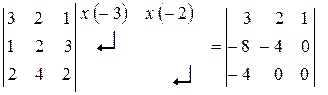
-16 = -16

Для обчислення визначників порядка n > 3 використовують алгебраїчне доповнення.

Мінором 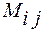елемента з визначника n-го порядку, називається визначник n-1 порядку, який одержуємо з визначника шляхом викреслювання і-го рядка та j-го стовпця, на перетині яких знаходиться елемент

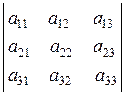
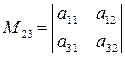
Алгебраїчним доповненням визначника називається мінор цього елемента, взятий зі знаком , тобто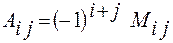

Приклад: Знайти алгебраїчні доповнення до елементів 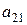та

визначника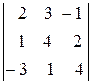

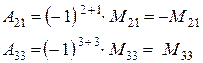
Теорема Лапласа (розкладання визначника за елементами будь-якого рядка або стовпця).

Визначник n-го порядку дорівнює сумі добутків усіх елементів будь-якого рядка (або стовпця) на відповідні їм алгебраїчні доповнення.

3. Для того, щоб обчислити визначник n-го порядку потрібно до нього застосовувати властивість 7 та теорему Лапласа.

Для скорочення обчислень визначника доцільно його розкласти за елементами такого рядка чи стовпця, який містить найбільшу кількість нулів.

У такому випадку не треба знаходити алгебраїчні доповнення до елементів, що дорівнюють 0 (добуток 0 на будь-яке алгебраїчне доповнення дорівнює 0). Треба навчитись виконувати еквівалентні перетворення визначника, які дають можливість одержати нулі у деякому рядку або стовпці.

Приклад: Обчислити визначник 4 порядку

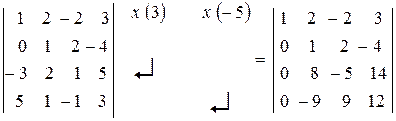
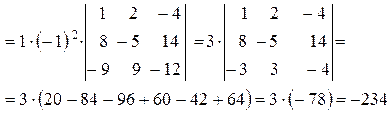
Дата добавления: 2014-12-07