
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Обчислення площ плоских фігур
|
|
|
|
Довжина дуги.
Х
A b
0 1 4
A b х
У
Довжина дуги.
П Л А Н
1. Обчислення площ плоских фігур.
3. Об’єм тіла обертання.
4. Площа поверхні обертання.
 |







 у=f (x)
у=f (x)
 |
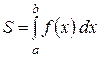

 1) 2)
1) 2)
у y







 y= f (x) y=
y= f (x) y= 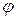 (x)
(x)


 y= f (x)
y= f (x)
 |  | ||||
 | |||||
 y=
y= 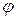 (x)
(x)
 | |||
 | |||
0 a b x 0 a c b x
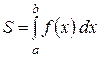



 3) 4) y a b
3) 4) y a b



 у a b
у a b




 х x
х x




 y=f (x)
y=f (x)
 |  | ||
y= 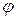 (x)
(x)
 y= f (x)
y= f (x)


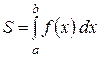

 Приклад: Обчислити площу фігури, обмеженої лініями ху=1, х=1, х=4, у=0.
Приклад: Обчислити площу фігури, обмеженої лініями ху=1, х=1, х=4, у=0.
 у
у
ху=1

 (кв. од.)
(кв. од.)
 3.
3.
у
 | |||
 |



 0 x
0 x
 |
 - об’єм тіла обертання навколо осі Ох.
- об’єм тіла обертання навколо осі Ох.
 |
у
d



 x=
x= 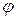 (y)
(y)

 - об’єм тіла обертання навколо осі Оy.
- об’єм тіла обертання навколо осі Оy.
Приклад: Обчислити об’єм тіла обертання навколо осі Ох трапеції, обмеженої лініями 
 у Тіло обертання має назву катеноїд
у Тіло обертання має назву катеноїд
 |
0 4 х
 |


 =
=
= 
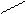
 =
= 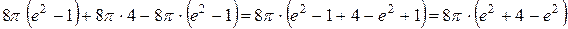 (куб. од.)
(куб. од.)
 2. у
2. у



 y= f (x)
y= f (x)
 |
0 a b х

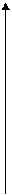 у
у
4.

0 a b x

Питання для самоконтролю
1. Обчислення площ плоских фігур.
3. Об’єм тіла обертання.
4. Площа поверхні обертання.
Л Е К Ц І Я 25
Тема: Невласні інтеграли.
Мета: ознайомити з нескінченними межами інтегрування (першого роду), невласного інтеграла від необмежених функцій (другого роду).
Література: [1, с. 385-394]; [6, с. 415-420].
1. Невласні інтеграли з нескінченними межами інтегрування (першого роду).
2. Невласні інтеграли від необмежених функцій (другого роду).
1. у

 1)
1)
 y= f (x)
y= f (x)
 0 а х
0 а х
Якщо верхня межа визначеного інтеграла  , то одержуємо невласний інтеграл з нескінченною верхньою межею інтегрування:
, то одержуємо невласний інтеграл з нескінченною верхньою межею інтегрування:


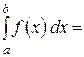



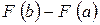
Якщо границя існує (дорівнює певному числу), то невласний інтеграл називається збіжним;
Якщо ж границя не існує або нескінченна – розбіжним.
 2) у
2) у

 y= f (x)
y= f (x)
 0 b х
0 b х


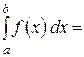


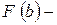

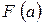
 3)
3)
y
 |
0 c x
 , с – довільне число
, с – довільне число
Даний інтеграл існує або є збіжним лише тоді, коли є збіжними обидва інтеграли – доданки. Якщо ж хоча б один з інтегралів розбіжний, то даний інтеграл також буде розбіжним.
2. у



 1)
1)

0 а b-  b x
b x
Нехай функція y=f (x) визначена на проміжку [a; b).
Точку b назвемо особливою точкою функції, якщо f (x)  при
при 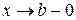
Невласним інтегралом від необмеженої функції (справа) називають
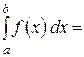

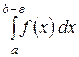 , де
, де 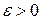 - довільне
- довільне
 2)
2)

 у
у
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 | |||||||||||||
 |  |  | |||||||||||

 0 а а+
0 а а+  b х
b х
Якщо  - особлива точка функції, то
- особлива точка функції, то
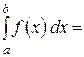


(функція необмежена зліва).



 3)у
3)у
 |  |
 0 а с b х
0 а с b х
Якщо f (x) необмежена в околі якої-небудь внутрішньої точки (розривна), то
 , с – точка розриву
, с – точка розриву
Приклад: 
= 
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 270; Нарушение авторских прав?; Мы поможем в написании вашей работы!