В векторной форме. где m - масса материальной точки;

L = [ r´p ] = [ r´ m v ], (1.56)

где m - масса материальной точки;

v - скорость материальной точки;

l – плечо (кратчайшее расстояние от направления импульса до оси вращения).

Момент импульса системы относительно неподвижной оси вращения z -проекция на эту ось вектора L (момента импульса системы):

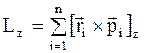, (1.57)

где r _i, p _i - радиус-вектор и импульс i-й материальной точки;

n - общее число точек в системе.

Связь момента импульса тела с вектором угловой скорости ω и моментом инерции:

L = I∙ ω. (1.58)

Основной закон динамики вращательного движения твердых (недеформирующихся) тел, для которых I = const (второй закон динамики для вращательного движения):

M = I∙ ε; . (1.59)

Импульс вращающего момента - произведение вращающего момента на время его действия:

M× dt = d L. (1.60)

Главные оси инерции – три взаимно перпендикулярных свободных оси вращения тела произвольной формы, проходящие через его центр масс.

Осциллятор – физическая система, совершающая колебания. Система, у которой величины, описывающие ее, периодически меняются с течением времени.

Гармонический осциллятор – механическая система, совершающая колебания около положения устойчивого равновесия, описывающие величины которой изменяются по гармоническому закону (закону синуса или косинуса).

Уравнение движения гармонического осциллятора:

, (1.61)

где a = d²x/dt² = - ω₀²x - ускорение материальной точки;

F - возвращающая сила, которая стремится вернуть систему в положение равновесия (F = - mω₀²x = - kx);

x – смещение;

k = mω₀² - коэффициент возвращающей силы. Он численно равен возвращающей силе, вызывающей единичное смещение.

Решение уравнения движения гармонического осциллятора:

x = x₀×sin(ω₀t + φ₀). (1.62)

Примеры гармонических осцилляторов: физический, математический и пружинный маятники:

а) пружинный маятник - тело массой m, подвешенное на пружине, совершающее гармоническое колебание.

Уравнение движения пружинного маятника:

; , (1.63)

где d²(Dl)/dt² = - ω₀²(Dl);

Dl – величина деформации.

Решение уравнения движения пружинного маятника:

Dl = (Dl)₀×sin(ω₀t + φ₀). (1.64)

Круговая частота, частота и период колебаний пружинного маятника:

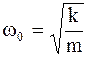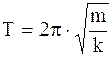; ; ; (1.65)

б) физический маятник - твердое тело, совершающее гармоническое колебательное движение относительно оси, не совпадающей с центром масс.

Уравнение движения физического маятника:

. (1.66)

Решение уравнения движения физического маятника:

j = j₀×sin(ω₀t + α), (1.67)

где α - начальная фаза колебаний.

Круговая частота, частота и период колебаний физического маятника:

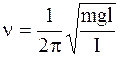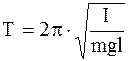; ; ; (1.68)

в) математический маятник - тело массой m, размерами которого можно пренебречь, подвешенное на невесомой, нерастяжимой нити.

Круговая частота, частота и период колебаний математического маятника:

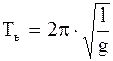; ; . (1.69)

Приведенная длина физического маятника - величина, численно равная длине такого математического маятника, период колебаний которого равен периоду колебаний физического маятника:

L_пр = I/ml. (1.70)

Затухающие (свободные) колебания - движения реальной колебательной системы, сопровождающиеся силами трения и сопротивления, которые приводят к уменьшению амплитуды колебаний. При этом энергия, потерянная системой, не восполняется за счет внешних сил.

Уравнение затухающих колебаний:

, (1.71)

где r - коэффициент сопротивления.

Решение уравнения затухающих колебаний:

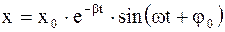, (1.72)

где А = x₀×e^-βt - амплитуда колебаний, убывающая по экспоненциальному закону;

β = r/(2m) - коэффициент затухания, характеризующий быстроту убывания амплитуды с течением времени;

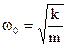– собственная частота колебаний системы, т.е. та частота, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (r = 0).

Круговая частота, частота и период затухающих колебаний:

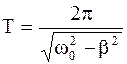; ; . (1.73)

Характеристики затухающих колебаний:

1) декремент затухания - отношение двух смещений, отличающихся друг от друга по времени на период. Декремент затухания характеризует быстроту затухания в зависимости от числа колебаний:

. (1.74)

2) логарифмический декремент затухания - величина, равная натуральному логарифму от декремента затухания. Логарифмический декремент затухания характеризует затухание колебаний за период:

l = lnD = ln(e^βΤ) = βT. (1.75)

Вынужденные колебания – колебания, совершаемые системами под действием внешней (вынуждающей) силы, изменяющейся по какому-либо закону, например гармоническому:

F = F ₀×sinwt, (1.76)

гдеF₀ - амплитудное значение вынуждающей силы;

w - частота вынуждающей силы.

Уравнение вынужденных колебаний:

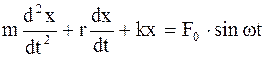. (1.77)

Решение уравнения вынужденных колебаний:

X = X₁ + X₂ = x₀×e^-bt×sin(ω't + φ₀') + x₀×sin(ωt + φ), (1.78)

где .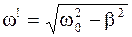

Амплитуда и начальная фаза вынужденных колебаний:

; (1.79)

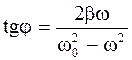. (1.80)

Резонанс – явление резкого возрастания амплитуды колебаний при некоторой определенной для данной системы частоте (резонансной частоте).

Резонансная частота

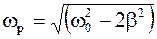. (1.81)

1.3. Энергия, работа, мощность

Энергия - количественная мера и качественная характеристика движения и взаимодействия материи во всех ее превращениях. Она является функцией состояния системы и характеризует способности системы к совершению работы при переходе из одного состояния в другое.

Изменение энергии при переходе системы из одного состояния в другое равно работе, совершаемой системой в процессе перехода:

DW = W₁ – W₂ = A. (1.82)

Диссипация (рассеяние) энергии механических систем -процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления).

Диссипативные системы -системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.

Механическая энергия - физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи.

Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения.

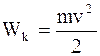. (1.83)

Кинетическая энергия системы - сумма кинетических энергий отдельных тел (материальных точек) этой системы:

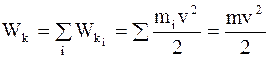, (1.84)

где m = åm_i - масса тела (системы);

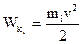- кинетическая энергия i-го тела системы.

Связь между кинетической энергией тела (системы) и его импульсом:

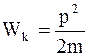. (1.85)

Кинетическая энергия при вращательном движении:

1) элементарной массы Dm_i:

, (1.86)

где I_i = Dm_i∙r_i² - момент инерции материальной точки, относительно выбранной оси вращения;

2) тела (системы):

, (1.87)

где - момент инерции тела относительно той же оси вращения.

Потенциальная энергия -физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе.

Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком:

dW_p = - dA. (1.88)

Потенциальная энергия тяготеющих масс:

. (1.89)

Потенциальная энергия системы «тело-Земля», если тело находится на некоторой высоте h над поверхностью Земли:

, (1.90)

где - потенциальная энергия системы «тело – Земля», если тело находится на поверхности Земли.

Изменение потенциальной энергии в том случае, когда тело поднимается на некоторую высоту h над поверхностью Земли:

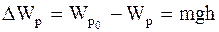. (1.91)

Потенциальная энергия упругой деформации:

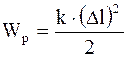. (1.92)

Связь потенциальной энергии материальной точки (тела, системы) во внешнем силовом поле с силой, действующей на материальную точку (тело, систему):

dWp = - F_r×dr, 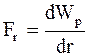. (1.93)

Дата добавления: 2014-12-07