Динамика потока в рабочем колесе, Уравнение Эйлера

Увеличение энергии перемещающегося через РК потока жидкости, т.е. появление напора, происходит путем силового воздействия на нее стенок каналов. Для осуществления этого воздействия необходимо приложить к вращающемуся валу момент внешних сил. Этот момент рассчитывается по теореме об изменении момента количества движения системы (МКДС) материальных точек. Момент количества движения системы относительно оси х - Кх равен алгебраической сумме моментов количества движения точек системы относительно той же оси. Если в качестве системы точек имеем тело определенной конфигурации, вращающееся вокруг оси х с угловой скоростью вращения ω, то МКДС рассчитывается как произведение момента инерции тела относительно оси вращения J_х на ω:

Кх = J_х ω.

Для кольца массой m и радиусом R - J_х = m R ² (относительно оси х, перпендикулярной плоскости кольца и проходящей через его центр), а при его вращении с угловой скоростью ω величина МКДС - Кх = m R V, где V= R ω –линейная скорость.

Согласно теореме об изменении МКДС: производная по времени момента количества движения системы относительно неподвижной оси равняется главному моменту внешних сил, действующих на материальные точки системы, вычисленному относительно той же точки.

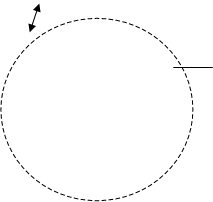
Применим эту теорему для установившегося движения потока в РК, равномерно вращающемуся с угловой скоростью вращения ω вокруг оси х, направленной к зрителю (см. рис. 4.1). Входные кромки лопастей РК размещены на окружности радиуса R _1, выходные – радиуса R ₂.

Сумма моментов действующих на поток жидкости Q _РК сил равна моменту, приложенному к валу насоса от двигателя - М, поскольку РК вращается равномерно.

Система материальных точек движущейся через РК жидкой среды представлена в произвольно выбранный момент времени τ и спустя бесконечно малый промежуток d τ. Обозначенные векторы абсолютных скоростей С ₁ и С ₂ формируются как результат вращения РК и перемещения жидкости в его межлопастном пространстве.

За промежуток времени d τ заполняющая МЛП масса жидкости переместится в радиальном направлении на расстояния dR ₁ и dR _2, что приведет к изменению МКДС на величину dКх.

Сравнение правого и левого рис. 4.1 позволяет для искомой величины dКх записать:

dКх = (К₂ + dК₂ ) - (К₂ + dК₁)= dК₂ -dК₁, (4.1)

где К ₂ –МКДС жидкости, находящейся окружностью радиуса R₂ и R₁+ dR_{1 ,}

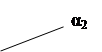
а dК ₂= dm₂ R₂ С₂ Cos α ₂

и dК₁= dm₁ R₁ С₁ Cos α ₁

МКДС бесконечно тонких колец, изображенных на рис. 4.1.

		dК 1

τ

dК ₁  

С2uС1u

С ₂  

С ₂

К ₂  

К ₂  

С₁

С ₁

ω

α ₁

Q _рк

R ₁  

R ₁

R ₂

dm₁ = dm₂= dm

τ+ d τ

dК ₃  

	Рис 4.1.

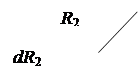В силу неразрывности потока жидкости элементарная масса выделенных колец, т.е. количество жидкости, перетекшей через РК за время d τ:

dm= dm₁ = dm₂= d( ρ Q _РК)= ρ Q _РК d τ, (4.2)

поэтому:

dК ₂ = dm₂ R ₂ С ₂ Cos α₂ = R ₂ С ₂ Cos α ₂ρ Q _РК d τ,

dК ₁ = dm ₁ R ₁ С ₁ Cos α₁ = R ₁ С ₁ Cos α₁ ρ Q _РК d τ.

Выполняя вычисления по зависимости (4.1) получаем производную и равный ей момент внешних сил:

dКх / d τ = М = ρ Q _РК(R ₂ С ₂ Cos α₂- R₁ С ₁ Cos α₁) = ρ Q _РК (R ₂ С ₂ u - R ₁ С ₁ u). (4.3)

Умножая левую и правую части 4.3 на ω получаем:

М ω = N _РК= ρ Q _РК (U ₂ С ₂ u -U ₁ С ₁ u), (4.4)

где U _2, U ₁ - окружные скорости на радиусах выхода и входа в РК,

а С₁ u и С ₂ u –соответствующие проекции абсолютной скорости на касательные к входной и выходной окружностям РК

С другой стороны, используя понятие мощности РК, аналогичное определению мощности насоса:

N _РК= ρ Q _РК g Н _РК (4.5)

и сопоставляя 4.4 и 4.5, получаем выражение для теоретического напора РК:

Н _РК,т.∞.= (U ₂ С 2 u - U ₁ С 1 u)/ g (*)

Это основное уравнение центробежного насоса называется уравнением Эйлера.

При его выводе предполагалось:

- отсутствие гидравлических потерь при течении,

- наличие осевой симметрии потока в виде бесконечного множества струй (т.е. бесконечного числа лопастей нулевой толщины), повторяющих геометрическую форму лопастей.

Наличие этих упрощающих допущений обозначается присвоением индексов т и ∞.

При отсутствии закрутки потока на входе в РК С₁u = 0 и уравнение (*) имеет вид:

Н _РК,т.∞.= U ₂ С 2 u / g (**)

Согласно определению напора, теоретическое давление записывается в виде:

Р _РК,т.∞.= ρ (U ₂ С ₂ u - U ₁ С ₁ u). (***)

Рассматривая параллелограммы скоростей центробежного колеса на входе и выходе из РК (см. рис. 3.2 а, б, в, г) при острых углах α и β, и вычисляя величины векторов W ₁ и W ₂ как гипотенузы прямоугольных треугольников, имеем:

W ²₁= U ²₁+ С ²₁ - 2 U ₁ С ₁ u,

W ²₂= U²₂+ С ²₂ - 2 U ₂ С ₂ u.

Подставляя из этих выражений произведения U Сu в соотношение (*), получим соотношение, раскрывающее механизм создания напора в центробежном РК:

Н _РК,т.∞.=[(U ²₂ - U ²₁) + (С ²₂ - С ²₁) + (W ²₁ - W ²₂)]/2 g (4.6)

Нетрудно видеть, что полный напор центробежного колеса складывается из двух:

-скоростного напора вследствие прироста абсолютной скорости частиц жидкости:

Н _{ск РК,}т.∞.= (С ²₂ - С ²₁) /2 g,

-статического напора, обусловленного работой центробежных сил и повышением давления за счет кинетической энергии относительного движения:

Н _{ст РК,}т.∞.= [(U ²₂ - U ²₁) + (W ²₁ - W ² 2)]/2 g.

При малых подачах, т.е. малых значениях W ≈ 0 и С ≈ U реализуется только напор, равный:

(С ²₂ - С ²₁) /2 g + (U ²₂ - U ²₁) /2 g = (U ²₂ - U ²₁) / g. (4.7)

Дата добавления: 2014-12-07