Информационные характеристики непрерывных

каналов связи [1 и др.].

Модели непрерывных каналов связи. Каналы, используемые для передачи непрерывных сигналов, принято называть непрерывными. Такие каналы до сих пор находят широкое применение, например, в технике телефонной связи, радиовещании.

Реальные непрерывные каналы представляют собой сложные инерционные нелинейные объекты, характеристики которых случайным образом изменяются во времени. Для анализа таких каналов разработаны математические модели различных уровней сложности и степени адекватности реальным каналам. Модели, получившие наиболее широкое распространение, - это разновидности гауссова канала.

Под гауссовым каналом понимают математическую модель реального канала, построенную при следующих допущениях:

1) основные физические параметры канала являются известными детерминированными величинами;

2) полоса пропускания канала ограничена частотой F_K, Гц;

3) в канале действует аддитивный гауссовый (имеющий нормальный закон распределения) белый шум – аддитивная флюктуационная помеха ограниченной мощности с равномерным частотным спектром и нормальным распределением амплитуд.

Предполагается также, что по каналу передаются сигналы с постоянной средней мощностью, статистические связи между сигналами и шумом отсутствуют, ширина спектра сигнала и помехи ограничена полосой пропускания канала.

При рассмотрении информационных характеристик канала (скорости передачи, пропускной способности, коэффициента использования) основное внимание будет уделено каналу.

Скорость передачи информации по непрерывному каналу. Скорость передачи информации по непрерывному каналу – это количество информации, которое передается в среднем принятыми непрерывными сигналами s(t), относительно переданных z(t) в единицу времени.

Поскольку полоса пропускания канала всегда ограничена, непрерывные сообщения на достаточно продолжительном интервале времени T с некоторой погрешностью могут быть представлены последовательностями отсчетов. С учетом наличия корреляционных связей между отсчетами и конечной верности воспроизведения, обусловленной воздействием помехи, для средней скорости R(SZ) передачи информации дискретизованным сигналом получим

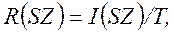(4.20)

где I(SZ) – количество информации, определяемое выражением, аналогичным (3.40).

По мере увеличения длительности T эта скорость возрастает, так как при каждом новом отсчете реализация уточняется. В пределе при T→∞ N-мерные распределения становятся бесконечными и выражение (4.20) будет определять среднюю [R(SZ)] скоростью передачи информации по непрерывному каналу:

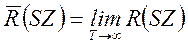
Переход к пределу при T→∞ также означает усреднение скорости по всем возможным сигналам.

Степень вредного воздействия помехи с известными статистическими свойствами на различные ансамбли входных сигналов различна. Вследствие этого различны и значения скорости передачи информации.

Пропускная способность непрерывного канала связи. Максимально возможную скорость C_Н передачи информации по непрерывному каналу с известными техническими характеристиками называют пропускной способностью непрерывного канала:

(4.21)

где максимум находят по всем возможным ансамблям плотности вероятности (дифференциальных законов распределения) входных сигналов

Так же, как и в случае дискретных каналов, скорость передачи информации по непрерывному каналу зависит от выбора ансамбля входных сигналов. Максимальная скорость передачи информации реализуется при максимальной скорости поступления информации на вход канала, которая соответствует случаю выбора ансамбля входных сигналов с максимальной энтропией. Для дискретных каналов, когда заданным для ансамбля сигналов является объем алфавита канала, максимальная скорость поступления информации обеспечивается при равномерном использовании символов алфавита. Для непрерывных сигналов, когда заданной следует считать среднюю мощность сигнала, максимальная скорость поступления информации соответствует использованию нормальных центрированных случайных сигналов. Условие центрированности обеспечивает при этом максимум дисперсии при заданной средней мощности сигнала, а его нормальность – наибольшую априорную энтропию каждого отсчета при данном значении дисперсии (см. п.3.4). Поэтому при определении пропускной способности непрерывного канала входных сигналов будем считать стационарными случайными центрированными нормальными.

Шум будем считать нормальным белым, что соответствует максимальной энтропии, вносимой шумом в полученное непрерывное сообщение, т.е. максимальной ненадежности канала по Шеннону при заданном отношении сигнал/шум. Принимаемый сигнал имеет вид:

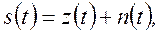(4.22)

где z(t) – передаваемый сигнал, несущий полезную информацию; n(t) – шумы в канале.

Ширина спектра сигнала ограничивается верхней частотой F_K, определяемой полосой пропускания канала. Поэтому согласно теореме Котельникова сигнал полностью определяется дискретными отсчетами s_i, следующими с частотой 2F_K. Значения белого шума при такой частоте отсчетов будет некоррелированными [13]. Дискретные отсчеты передаваемого сигнала будем также считать некоррелированными, что соответствует условию максимума его энтропии (для нормальных сигналов, как было показано в п.3.4, некоррелированность отсчетов означает и их независимость). Тогда и дискретные отсчеты принимаемого сигнала будут некоррелированными (а значит, и независимыми), и количество информации, содержащейся в принимаемом сигнале, будет равно сумме количеств информации, содержащихся в независимых его отсчетах, следующих с частотой 2F_K. Количество информации о текущем значении передаваемого сигнала z_i, вносимое дискретным отсчетам принимаемого сигнала s_i, может быть представлено в виде разности априорной энтропии этого отсчета и апостериорной его энтропии при известном отсчете передаваемого сигнала. Заменяя разности энтропий разность соответствующих дифференциальных энтропий по [13], получаем информацию вносимую общим дискретным отсчетом сигнала

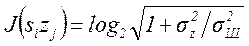(4.23)

где σ²_ш – дисперсия шума, имеющего нормальное распределение, а величина σ²_z/σ²_ш=P_c/P_ш характеризует отношение сигнал/шум в канале.

Пропускная способность канала, определяемая количеством информации, передаваемой по каналу в единицу времени при рассмотренных условиях, равна информации, содержащейся в 2F_K независимых дискретных отсчетах сигнала:

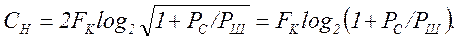(4.24)

Формула (4.24) называется формулой Шеннона.

Если распределение аддитивной помехи не является нормальным или же спектр ее неравномерный (шум не белый, и имеется корреляция между его отсчетами), то формула (4.24) занижает пропускную способность канала.

Нетрудно видеть, что при P_c/P_ш→0 С_Н→0. Формулу (4.24) можно трактовать следующим образом. Величина (1+ P_c/P_ш) характеризует количество уровней непрерывного сигнала, различимых на фоне шума при данном отношении P_c/P_ш. Поэтому количество информации, приходящееся на один отсчет, будет в данном случае таким же, как для дискретного источника с числом состояний (1+ P_c/P_ш).

Преобразуем (4.24), приняв P_ш=N₀F_K, где N₀ – спектральная плотность белого шума (для одностороннего спектра):

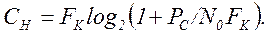(4.25)

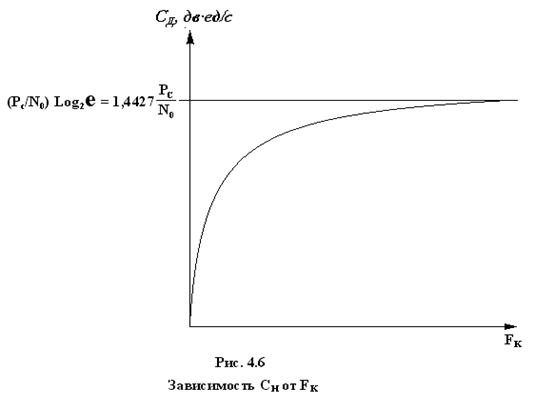
Раскрывая по правилу Лопиталя неопределенность при F_K→∞, в правой части (4.25) получаем C_H=(P_C/N₀)log₂e, т. е. пропускная способность стремится к фиксированной величине, определяемой отношением средней мощности сигнала к спектральной плотности шума. Таким образом, обмен мощности сигнала на полосу пропускания для обеспечения заданной пропускной способности непрерывного канала возможен лишь в некоторых границах, за которыми дальнейшее расширение полосы пропускания дает уже малый эффект.

О характере зависимости C_H=f(F_K) можно судить по графику на рис. 4.6

4.4 Согласование физических характеристик сигнала и канала [1 и др.].

Конкретный канала связи обладает определенными физическими параметрами, от которых зависит возможность передачи по нему тех или иных сигналов. Независимо от назначения непрерывного канала его можно характеризовать тремя основными параметрами: временем, в течении которого он предоставляется для передачи сигнала T_K, шириной полосы пропускания сигнала F_K и допустимым превышением сигнала над помехой в канале H_K. Превышение H_K характеризуется разностью максимально допустимого сигнала в канале P_Zmax и уровня помехи P_Ш (в логарифмическом масштабе). Для проводных каналов превышение в основном определяется пробивным напряжением и уровнем перекрестных помех, для радиоканалов – возможностями выявления сигнала на соответствующих расстояниях.

Произведение указанных основных параметров канала связи принято называть объемом (емкостью) канала и обозначать V_K:

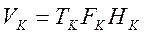(4.26)

При оценке возможностей передачи сигнала по каналу с заданными физическими характеристиками также ограничиваются рассмотрением трех основных параметров сигнала: его длительности T_C, ширины спектра F_C и превышения над помехой H_C, причем

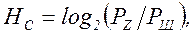(4.27)

где P_Z – средняя мощность передаваемого сигнала; P_Ш – средняя мощность помехи (шума) в канале.

Превышение H_C связано с возможностями передатчика и дальностью передачи. Чем больше H_C, тем меньше вероятность ошибочного приема. Аналогично объему канала вводится понятие объема (емкости) V_С передаваемого сигнала:

(4.28)

Как объем сигнала, так и объем канала может быть представлен в трехмерном пространстве с соответствующими координатами T, F, H (рис. 4.7).

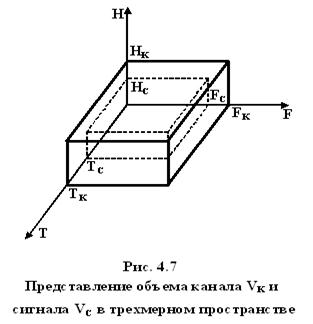
Необходимым условием принципиальной возможности неискаженной передачи сигнала по данному каналу является выполнение соотношения

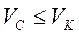(4.29)

При этом, однако, могут потребоваться преобразования для обеспечения достаточных условий передачи, а именно

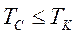
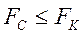
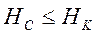(4.30)

Когда канал имеет меньшую полосу пропускания, чем практическая ширина спектра, подлежащего передаче сигнала, последнюю можно уменьшить за счет увеличения длительности сигнала. Объем сигнала при этом сохраняется неизменным. Практически такое преобразование можно осуществить, например, посредством записи сигнала на магнитную ленту с высокой скоростью, при которой ширина его спектра равна полосе пропускания канала.

Если, наоборот, широкополосный канал представляется на время меньшее длительности сигнала, то согласования осуществляется за счет расширения спектра сигнала. Для реализации также можно использоваться накопитель на магнитной ленте, однако в данном случае скорость воспроизведения должна быть выше скорости записи.

При низком доступном уровне превышения сигнала в канале преобразование заключается в уменьшении уровня превышения передаваемого сигнала с одновременным увеличением его длительности путем многократного повторения передачи. Возможны и другие виды преобразования.

Рассмотрим, какова связь между объемом канала и количеством информации, которое можно получить о передаваемом по этому каналу сигнале.

Предельное количество информации, которое может быть передано по каналу связи за время T_K,

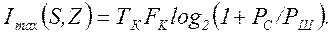(4.31)

Отсюда следует, что если P_C/P_Ш » 1, то при условии обеспечения посредством преобразования сигнала полного использования физических возможностей канала максимальное количество информации, которое можно получить о сигнале, близко к емкости канала:

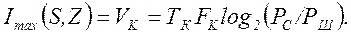(4.32)

4.5 Согласование статистических свойств источника сообщений и канала связи [1 и др.].

Согласование статистических свойств и отражающих их информационных характеристик источника сообщений и канала связи проводится с целью улучшения качества системы передачи. Оценка качества осуществляется по трем основным показателям: достоверности, средней скорости передачи и сложности технической реализации системы, определяющей ее стоимость и надежность. Хотя с точки зрения практики сложность технической реализации может иметь решающее значение, при определении предельных возможностей системы целесообразно ограничится только первыми двумя показателями.

Достоверность дискретного канала обычно оценивается значением вероятности ошибочного приема одного символа (элементарного символа). В случае передачи непрерывного сообщений о достоверности судят по значению среднеквадратической ошибки при воспроизведении сообщения

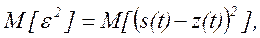
где s(t) – сообщение, поступающее с выхода канала; z(t) – сообщение на входе канала.

Достоверность характеризует помехоустойчивость информационной системы.

Под скоростью передачи подразумевается среднее количество информации, передаваемое по каналу в единицу времени. Именно эта (а не техническая) скорость формирования символа подлежит согласованию с пропускной способности канала.

Скорость передачи информации характеризует эффективность системы.

Если высоких требований в отношении скорости передачи и достоверности к системе передачи не предъявляется, то согласование статистических (информационных) характеристик источника сообщений и канала связи не является принципиально необходимым.

При преобразовании сообщений в сигналы в этом случае могут преследоваться две основные цели. Одна из них заключается в том, чтобы преобразовать сообщения в такую систему символов (код), чтобы она обеспечивала простоту и надежность аппаратурной реализации информационных устройств, и приемлемую их эффективность: простоту аппаратуры различения элементарных сигналов, соответствующих отдельным символам, приемлемое время при их передаче, простоту выполнения в этой системе арифметических и логических действий. Техническая реализация процесса кодирования в таким простейшем виде при непрерывном входном сигнале осуществляется аналого-цифровыми преобразователями.

Другой целью преобразования сообщений является защита их от несанкционированного доступа. Такое преобразование называют шифрованием. Оно может проводится как на уровне знаков, так и на уровне символов.

В случае отсутствия необходимости в статистическом согласовании источника сообщений с каналом связи вопрос повышения качества функционирования системы решаются для дискретного канала от входа модулятора до выхода демодулятора.

Считается, что символы на входе модулятора поступают равновероятно и статистические связи между ними отсутствуют. Из множества сигналов, удовлетворяющих заданным ограничениям по мощности и полосе частот, для отображения символов отбираются такие, которые в предположении воздействия на них аддитивного гауссова шума обеспечивают наибольшую достоверность приема каждого отдельного символа. Одновременно определяется структура оптимального приемника. Наиболее полно эти вопросы рассмотрены для случая двоичного канала (m=2).

Увеличение эффективности и помехоустойчивости системы передачи информации, как показал Шеннон, возможно за счет введения в канал связи кодирующего, а следовательно, и декодирующего устройств, цель которых состоится в статистическом согласовании свойств источника сообщений и канала связи.

Доказанными им теоремами обосновано существование оптимального способа кодирования, при котором достигается скорость передачи информации, сколь угодно близкая к пропускной способности данного канала связи. Под способом кодирования при этом подразумевается совокупность операций по преобразованию сообщений в сигналы и обратного преобразования смеси сигнала с помехами в сообщения, включая операции в частности канала «модулятор-демодулятор».

4.6 Контрольные вопросы к разделам 3 и 4 в форме «Задание – тест»

ТЕМА: «Количественная оценка информации».

1. Определите количество возможных сообщений источника, создаваемых из «m» равновероятных элементов для данного источника, по «n» букв в комбинации определяется как:

1) mⁿ; 2)m∙n; 3)m+n.

2. Количественная мера неопределенности определяется по формуле Хартли: H(x) = logM (где М = mⁿ, здесь m – число возможных равновероятных элементов источника, n число букв в комбинации) при основании логарифма 2 имеет меру (размерность) измерения:

Дата добавления: 2014-12-07