Кодирование как процесс выражения информации в цифровой форме

С точки зрения теории информации кодирование есть процесс сопоставления элементов алфавита источника цифрам. Правило сопоставления называется кодом. Цифры, сопоставленные элементам алфавита, называются кодовыми словами. Например, измерение аналоговой величины, выражающееся в сравнении ее с образцовыми мерами, также приводит к числовому представлению информации. Передача или хранение сообщений при этом сводится к передаче или хранению чисел. Числа можно выразить в какой-либо системе счисления. Таким образом, будет получен один из кодов, основанный на данной системе счисления.

Сравним системы счисления и построенные на их основе коды с позиций применения в системах передачи, хранения и преобразования информации.

Общепризнанным в настоящее время является позиционный принцип образования системы счисления. Значение каждого символа (цифры) зависит от его положения – позиции в ряду символов, представляющих число.

Единица каждого следующего разряда больше единицы предыдущего разряда в m раз, где m – основание системы счисления. Полное число получаем, суммируя значения по разрядам:

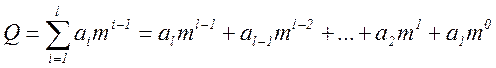
где i – номер разряда данного числа; – количество разрядов; a_i – множитель, принимающий любые целочисленные значения в пределах от 0 до m-1 и показывающий, сколько единиц i-го разряда содержится в числе.

Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи.

Однако с ростом основания существенно повышаются требования к линии связи и аппаратуре создания и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.

Учитывая оба обстоятельства, целесообразно выбирать систему, обеспечивающую минимум произведения количества различных символов m на количество разрядов l для выражения любого числа. Найдем этот минимум по графику и таблице на рис. 5.1, где показана связь между величинами m и l при воспроизведении определенного достаточно большего числа Q (Q ≈ 60000).

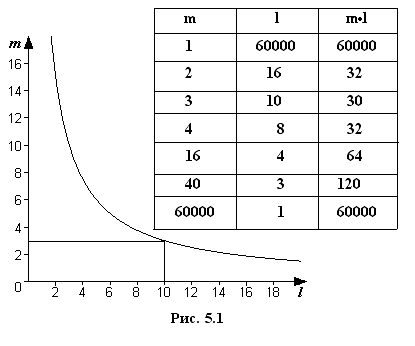
Зависимость m от l для представления числа Q = 60000.

Из графика следует, что наиболее эффективной системой является система с основанием три. Незначительно уступают ей двоичная и четверичная системы. Системы с основанием 10 и более существенно менее эффективны. Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе. Действительно, логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов сводится в этом случае к задаче обнаружения (если импульс или нет импульса), что значительно проще.

Арифметические и логические действия также наиболее просто осуществляется в двоичной системе. В таблицы сложения, вычитания и умножения входит всего по четыре равенства:

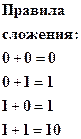
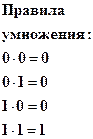
Наиболее распространенная при кодировании и декодировании логическая операция – сложение по модулю. В двоичной системе она также наиболее проста и определяется равенствами:

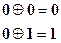
Алгоритм перевода из двоичной в привычную для человека десятичную систему несложен. Пересчет начинается со старшего разряда. Если в следующем разряде стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу.

Пример 5.1 Найдем десятичный эквивалент двоичного числа 1001. После первой единицы слева стоит 0. Удваиваем эту единицу. Получаем число 2. Цифрой следующего младшего разряда также является 0. Удваивая число 2, получаем 4. В самом младшем разряде стоит единица. Удваивая число 4 и прибавляя 1, окончательно получаем 9.

Итак, для передачи и проведения логических и арифметических операций наиболее целесообразен двоичный код. Однако он неудобен при вводе и выводе информации, так как трудно оперировать с непривычными двоичными числами. Кроме того, запись таких чисел на бумаге оказывается слишком громоздкой. Поэтому, помимо двоичной, получили распространение системы, которые, с одной стороны, легко сводятся как к двоичной, так и к десятичной системе, а с другой стороны, дают более компактную запись. К таким системам относятся восьмеричная, шестнадцатеричная и двоично-десятичная.

В восьмеричной системе для записи всех возможных чисел используется восемь цифр от 0 до 7 включительно. Перевод чисел из восьмеричной системы в двоичную крайне прост и сводится к замене каждой восьмеричной цифры равным ей трехразрядным двоичным числом. Например, для восьмеричного числа 745 получаем:

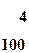
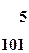
Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании.

Чтобы сохранить преимущества двоичной системы и удобство десятичной системы, используют двоично-десятичные коды. В таком коде каждую цифру десятичного числа записывают в виде четырехразрядного двоичного числа (тетрады). С помощью четырех разрядов можно образовать 16 различных комбинаций, из которых любые 10 могут составить двоично-десятичный код. Наиболее целесообразным является код 8-4-2-1 (табл. 5.1). Этот код относится к числу взвешенных кодов. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Двоично-десятичный код обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.

В табл. 5.1 представлены два других двоично-десятичных кода с весами 5-1-2-1 и 1-4-2-1, которые широко используются при поразрядном уравновешивании в цифровых измерительных приборах.

Среди кодов, отходящих от систем счисления, большое практическое значение имеют такие, у которых при переходе от одного числа к другому изменение происходит только в одном разряде.

Таблица 5.1

Число в десятичном коде	Двоично-десятичный код с весами 8-4-2-1	Двоично-десятичный код с весами 5-1-2-1	Двоично-десятичный код с весами 2-4-2-1
	0000 0000	0000 0000	0000 0000
	0000 0001	0000 0001	0000 0001
	0000 0010	0000 0010	0000 0010
	0000 0011	0000 0011	0000 0011
	0000 0100	0000 0111	0000 0100
	0000 0101	0000 1000	0000 1011
	0000 0110	0000 1001	0000 1100
	0000 0111	0000 1010	0000 1101
	0000 1000	0000 1011	0000 1110
	0000 1001	0000 1111	0000 1111
	0001 0000	0001 0000	0001 0000

Наибольшее распространение получил код Грея, часто называемый циклическим или рефлексно-двоичным. Код Грея используется в технике аналого-цифрового преобразования, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в табл. 5.2.

Правила перевода числа из кода Грея в обычный двоичный сводится к следующему: первая единица со стороны старших разрядов остается без изменения, последующие цифры (0 и 1) остаются без изменения, если число единиц, им предшествующих, четно, инвертируется, если число единиц нечетно.

Таблица 5.2

Число в десятичном коде	Код Грея	Число в десятичном коде	Код Грея	Число в десятичном коде	Код Грея

Пример 5.2. Выразим кодовое число единиц, записанное в коде Грея, в обычном двоичном коде.

Первая единица слева переписываем. Следующая цифра будет единицей, так как в этом разряде кода Грея стоит нуль и впереди только одна единица. Далее необходимо записать нуль, так как в следующем разряде исходного числа стоит единица и впереди снова имеется только одна единица. Поскольку перед последней цифрой числа в коде Грея стоят две единицы, то она должна остаться неизменной, т.е. нулем. Таким образом, число 1010 в коде Грея соответствует обычное двоичное число 1100.

5.2. Классификация кодов [4 и др.].

Теория кодирования развивается в двух главных направлениях: во-первых, поиск кодов, позволяющих в каналах без шумов максимально устранить избыточность источника (экономное кодирование) и тем самым повысить эффективность системы передачи информации, и, во-вторых поиск кодов, повышающих верность в канале с шумами (помехоустойчивое кодирование). Помехоустойчивые коды называют также корректирующими (они способны обнаруживать или исправлять ошибки и стирания канала), они возможны лишь при внесении определенной избыточности в используемых кодовых последовательностях.

При помехоустойчивом кодировании чаще считают, что избыточность источника на входе кодера K_И=0. Для этого имеются следующие основания: во-первых, очень многие дискретные источники (например, информация на выходе ЭВМ) обладают малой избыточностью; во-вторых если избыточность источников существенна, она обычно порождается сложными связями, которые в месте приема затруднительно использовать для повышения верности. Разумно поэтому в таких случаях сначала по возможности уменьшить избыточность первичного источника, а затем методами помехоустойчивого кодирования внести такую избыточность в сигнале, которая позволяет достаточно простыми средствами поднять верность.

Из сказанного следует, что экономное кодирование вполне может сочетаться с помехоустойчивым.

Коды можно классифицировать по весьма различным признакам. Одним из основных является основание кода m или число различных используемых в нем символов. Наиболее простыми являются двоичные (бинарные) коды, у которых m=2. Коды с m>2 называют многопозиционными. Мы будем интересоваться в основном двоичными кодами, нашедшими преимущественное применение на практике.

Далее коды можно разделять на блочные и непрерывные. Блочными называют коды, в которых каждый элемент («буква»)сообщения a_k(k=1, 2, 3, …, K) преобразуется в определенную последовательность (блок) кодовых символов {b_i}, называемую кодовой комбинацией b_k(k=1, 2, 3, …, K). Непрерывные коды образуют последовательность символов {b_i}, не разделяемую на последовательные кодовые комбинации: здесь в процессе кодирования символы определяются не одним, а целой группой элементов сообщения.

Пока что на практике чаще всего используются блочные коды, равномерные и неравномерные. В равномерных кодах, в отличие от неравномерных, все кодовые комбинации содержат одинаковое число символов (разрядов), передаваемых по каналу элементарными сигналами неизменной длительности. Это обстоятельство существенно упрощает технику передачи и приема сообщений и повышает помехоустойчивость системы связи.

Ко всякому коду обязательно предъявляется требование однозначности декодирования. В случае блочных кодов это значит, что всякой последовательности или группе последовательностей кодовых символов должна однозначно соответствовать последовательность элементов передаваемого сообщения, что всегда выполняется при использовании равномерных кодов.

Если объем (число возможных элементов-букв) алфавита источника сообщений равен K, то каждую букву можно закодировать с помощью n- разрядного равномерного кода с основанием m при

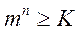(5.2)

Если в (5.2) имеет место равенство, т.е. все возможные кодовые комбинации используются для передачи сообщений, то в этом случае код называется безызбыточным или примитивным. Если же число возможных кодовых комбинаций больше числа различных букв и, следовательно, часть из них можно не задействовать при передачи сообщений, код называется избыточным или корректирующим.

5.3. Представление кодов [4 и др.].

Всякий блочный код можно представить:

- в виде таблицы;

- графически с помощью, так называемого «кодового дерева» (понятие «кодового дерева» является частным случаем более общего понятия – граф. При решении многих практических задач широко используется математическая теория графов [12]);

- аналитически с помощью полиномов, матриц, множеств и т.п.;

- и других способов.

Представление в виде таблицы основано на том, что в ней каждой букве, цифре алфавита источника сообщений сопоставляется определенная кодовая комбинация.

Для алфавита, содержащегося 8 букв (цифр), при равномерном десятичном, четверичном и двоичном кодах показано в таблице 5.3

Таблица 5.3

Буква	Число	m=10	m=4	m=2
А
Б
В
Г
Д
Е
Ж
З

Помимо представления таблицей, код очень часто представляют графически с помощью так называемого «кодового дерева».

Рассмотрим построение кодового дерева для наиболее простого и наиболее распространенного двоичного кода.

Для этого, начиная с определенной точки(«корня»), будем проводить отрезки прямой (ветви), наклоненные влево или вправо, если кодовым символом является соответственно «0» или «1». На рис. 5.2 построено три «кодовых дерева» для двоичного кода из табл. 5.3. На вершинах этого дерева написаны буквы алфавита источника, соответствующие данным кодовым комбинациям. Обратим внимание на то, что здесь каждой букве соответствует своя вершина «кодового дерева». С помощью «кодового дерева» (рис. 5.2 а) можно однозначно декодировать любую последовательность символов, если только она принята с самого начала. Это справедливо для любого равномерного кода.

Рассмотри теперь неравномерный двоичный код. Пусть он, например, задан «кодовым деревом» (рис. 5.2. б). В данном случае некоторым буквам сообщения соответствуют не вершины, а узловые точки дерева. Но тогда декодирование будет неоднозначным. Действительно, приняв в начале кодовой последовательности символ «0», мы не знаем, означает ли он букву «Б» или является началом кодовой комбинации, означающей буквы «Д» или «Е».

Однако можно построить неравномерные коды, допускающие однозначное декодирование, для этого достаточно, чтобы в кодовом дереве всем буквам источника соответствовали бы только вершины. Тогда ни одна кодовая комбинация не будет являться началом другой, более длинной комбинации. Такой код называется неприводимым.

Пример неприводимого кода представлен «кодовым деревом» (рис. 5.2 в). Если последовательность символов принятая с начала, то, начав при декодировании движение с «корня дерева», мы сумеем образовать законченную кодовую комбинацию только дойдя до какой-либо вершины. Затем мы возвращаемся к «корню дерева», выполняем декодирование следующей кодовой комбинации и т.д. Заметим, что всякий равномерный код является неприводимым.

Аналитически формирование кодовых комбинаций основано на отображении кодовых слов элементами алгебры полиномов. Комбинации, например корректирующего циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:

(5.3)

Для того чтобы в результате операций, используемых для формирования циклических кодов, получились полиномы, описывающие данный код, при всех операциях над полиномами должны выполнятся два условия:

1) действия над коэффициентами полиномов (сложение, вычитание, умножение на символ λ) должны производится по модулю m; 2) умножение полиномов должно производится по модулю Zⁿ-1, т.е. за результат умножения должен приниматься остаток от деления обычного произведения полиномов на двучлен Zⁿ-1. Первое условие необходимо для того, чтобы коэффициенты получаемых полиномов принадлежали алфавиту канала, а второе – чтобы степень этих полиномов соответствовала длине данного кода n.

5.4. Оптимальное (эффективное) статистическое кодирование [3 и др.].

При передаче знаки сообщений источника преобразуются в последовательность двоичных сигналов. Учитывая статистические свойства источника сообщений, можно минимизировать среднее число символов, требующихся для выражения одного знака сообщения, что при отсутствии шума позволяет уменьшить время передачи или объем запоминающего устройства.

Одной из характеристик сообщений является избыточность. Коэффициент избыточности определяется как

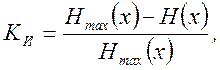(5.4)

где H(x) – энтропия, которую имеет сообщение источника; H_max(x) – максимальная энтропия.

Под избыточным понимают такие сообщения, для представления которых используются больше символов, чем это минимально необходимо. Решение задачи устранения избыточности сообщений выполняется с помощью эффективного кодирования.

Статистическое (оптимальное) кодирование сообщений для передачи их по дискретному каналу без помех базируется на теореме К. Шеннона, которую можно сформулировать так [3]: «Если производительность источника , где ε – сколь угодно малая величина, то всегда существует способ кодирования, позволяющий передавать по каналу все сообщения источника». Передачу всех сообщений при 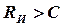осуществить невозможно.

Смысл теоремы сводится к тому, что как бы ни была велика избыточность источника, все его сообщения могут быть переданы по каналу, если 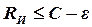. Здесь С – пропускная способность. По определению пропускная способность

(5.5)

где R_max – максимальная скорость передачи информации.

Кодирование по методу Шеннона-Фано-Хаффмена называется оптимальным, так как при этом повышается производительность дискретного источника

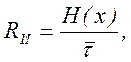(5.6)

где 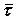- средняя длительность сообщения и наилучшим образом используется пропускная способность канала без помех.

Структура оптимального кода зависит от статистических характеристик источника, так и от особенности канала. Оптимальное кодирование называют статистическим потому, что для реализации кодирования необходимо учитывать вероятности появления на выходе источника каждого элемента сообщения (учитывать статистику сообщений).

Рассмотрим основные принципы оптимального (эффективного) кодирования на примере источника независимых сообщений X={x₁, x₂, …, x_r}. Под элементами множества X можно понимать, например, буквы алфавита естественного языка, пары, тройки и вообще любые блоки символов какого-либо алфавита, слова, предложения – словом, любые знаки.

Источник независимых сообщений необходимо согласовать с двоичным каналом без помех. При этих условиях процесс кодирования заключается в преобразовании сообщений источника в двоичные кодовые комбинации. Поскольку имеет место однозначное соответствие между сообщениями источника и комбинациями кода, то энтропия кодовых комбинаций: H(u), где u -выходной алфавит, равна энтропии источника

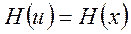(5.7)

а скорость передачи информации в канале

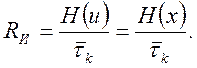(5.8)

здесь - средняя длительность кодовой комбинации, которая в общем случае неравномерного кода определяется выражением

(5.9)

где 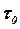- длительность одного элемента кода и 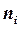- число элементов в комбинации, присеваемой сообщению .

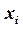Подстановка в формулу (5.8) выражений энтропии H(x) [] и (5.9) приводит к соотношению

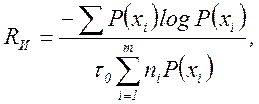(5.10)

в котором числитель определяется исключительно статистическими свойствами источника, а величина τ₀ – характеристика канала. При этом возникает вопрос, можно ли так закодировать сообщения, чтобы скорость передачи R достигала своего максимального значения, равного пропускной способности двоичного канала

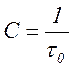(5.11)

Легко заметить, что это условие выполняется, если

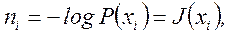(5.12)

где J(x_i) – количество информации в x_i сообщении.

Из (5.12) следует, что количество символов в кодовом слове соответствует минимальному 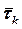и максимальному R. Очевидно, выбор n_i<J(x_i) не имеет смысла, так как в этом случае R>C, что противоречит выше доказанному утверждению теоремы Шеннона.

5.4.1 Методы эффективного кодирования некоррелированной последовательности знаков [1 и др.].

Для случая отсутствия статистической взаимосвязи между знаками конструктивные методы построения эффективных кодов были даны впервые американскими учеными Шенноном и Фано. Их методики существенно не различаются и поэтому соответствующий код получил название кода Шеннона – Фано.

Методика построения кода Шеннона – Фано [1].

Код строят следующим образом: знаки алфавита сообщений выписываются в таблицу в порядке убывания вероятности. Затем их разделяют на две группы так, чтобы суммы вероятностей каждой из групп были по возможности одинаковы. Всем знакам верхней половины в качестве первого символа приписывают 0, а всем нижним – 1. Каждую из полученных групп, в свою очередь, разбивают на две подгруппы с одинаковыми суммарными вероятностями и т.д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одному знаку.

Пример 5.3 Проведем эффективное кодирование ансамбля из восьми знаков с вероятностями, которые представлены в таблице 5.4.

Знаки xi	Вероят- ность P(xi)	Группы	Комбина-ция	ni	J(xi)
I	II	III	IV	V	VI	VII
x1	1/2	0							0	1	1
x2	1/4	1	0						10	2	2
x3	1/8	1	1	0					110	3	3
x4	1/16	1	1	1	0				1110	4	4
x5	1/32	1	1	1	1	0			11110	5	5
x6	1/64	1	1	1	1	1	0		111110	6	6
x7	1/128	1	1	1	1	1	1	0	1111110	7	7
x8	1/128	1	1	1	1	1	1	1	1111111	7	7

Таблица 5.4.

Ясно, что при обычном (не учитывая статистических характеристик) кодирования для представления каждого знака требуется три двоичных символа. Используя методику Шеннона – Фано, получаем совокупность кодовых комбинаций, приведенных в таблице 5.4.

При заданном распределении вероятностей сообщений код получается неравномерным. Его комбинации имеют различное число элементов n_i, причем, как ни трудно заметить, такой способ кодирования обеспечивает выполнения условия (5.12) полностью для всех сообщений.

В неравномерных кодах при декодировании возникает трудность в определении границ между комбинациями. Для устранения возможных ошибок обычно применяются специальные знаки. Так, в коде Морзе между буквами предается разделительный знак в виде паузы длительностью в одно тире. Передача разделительных знаков занимает длительное время, что снижает скорость передачи информации.

Важным свойством кода Шеннона – Фано является то, что ни смотря на его неравномерность, здесь не требуется разделительных знаков. Это обусловлено тем, что короткие комбинации не являются началом наиболее длинных комбинаций. Указанное свойство легко проверить на примере любой последовательности:

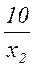
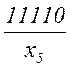
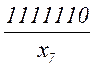
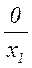
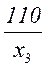
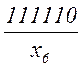
Таким образом, все элементы закодированного сообщения несут полезную информацию, что при выполнении условия (5.12) позволяет получить максимальную скорость передачи. Она может быть найдена также путем непосредственного вычисления по формуле (5.10)

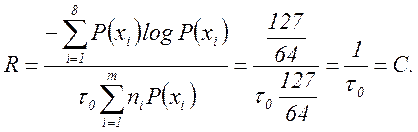(5.13)

Для сравнения рассмотрим кодирование тех же восьми сообщений {x₁, x₂, …, x₈} с применением обычного равномерного двоичного кода. Количество комбинаций при этом определяется выражением M=2ⁿ, где n – число элементов в комбинации. Так как M = 8, то n = log(M) = 3, а длительность каждой комбинации 3τ₀. Производя вычисления по аналогии с (5.13), получим

(5.14)

Пропускная способность в этом случае используется только частично. Из выражения (5.12) вытекает основной принцип оптимального кодирования. Он сводится к тому, что наиболее вероятным сообщениям должны присваиваться короткие комбинации, а сообщениям с малой вероятностью – более длинные комбинации.

Возможность оптимального кодирования по методу Шеннона – Фано доказывает, что сформулированная выше теорема справедлива, по крайней мере, для источников независимых сообщений. Теорема Шеннона может быть доказана и для общего случая зависимых сообщений.

Рассмотренная методика Шеннона – Фано не всегда приводит к однозначному построению кода. Ведь при разбиении на подгруппы можно сделать большей по вероятности, как верхнюю, так и нижнюю подгруппы. Например, множество вероятностей приведенных в таблице 5.5 можно было бы разбить двумя вариантами.

Таблица 5.5.

Знаки	x1	x2	x3	x4	x5	x6	x7	x8
Вероятности	0.22	0.2	0.16	0.16	0.1	0.1	0.04	0.02
Вариант	I	|-------------------------| |---------------------------------------------------|
II	|----------------| |------------------------------------------------------------|

От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшим для данного распределения вероятностей средним числом символов на букву.

Методика построения кода Хаффмена [2 и др.].

Для двоичного кода методика сводится к следующему алгоритму 1:

Шаг 1. Буквы алфавита сообщении X={x₁, x₂, …, x_r}, имеющие соответствующие вероятности их появления p(x₁), p(x₂), …, p(x_r), выписывают в основной столбец в порядке убывания вероятностей.

Шаг 2. Две последние самые маловероятные буквы x_r-1 и x_r объединяют в одну вспомогательную (укрупненную) букву а, которой приписывают суммарную вероятность, равную сумме вероятностей букв x_r-1 и x_r, т.е. p(a)=p(x_r-1)+p(x_r). Вероятности букв, не участвовавших в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце.

Шаг 3. Повторяем шаги 1 и2 до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.

Шаг 4. Для наглядности строим дерево. Двигаясь по кодовому дереву от корня к вершинам, т.е. сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию.

Пример 5.4. Используя методику Хаффмена, осуществим эффективное кодирование ансамбля знаков, приведенных в таблице 5.6.

Процесс кодирования в соответствии выше приведенному алгоритму поясняется таблицей 5.6. Для составления кодовой комбинации, соответствующей данному знаку, необходимо проследить путь знака по строкам и столбцам таблицы.

Таблица 5.6.

Знаки	Вероят-ности	Вспомогательные столбцы
1	2	3	4	5	6	7
z1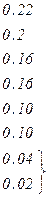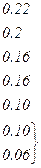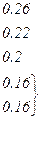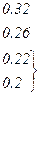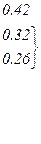
z2
z3
z4
z5
z6
z7
Z8

Для наглядности строим кодовое дерево. Из точки, соответствующей вероятности 1, направляем на две ветви, причем ветви с большей вероятностью присваиваем символ 1, а меньшей 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдет до вероятности каждой буквы. Кодовое дерево для алфавита букв, рассматриваемого в таблице 5.6, представлено на рисунке 5.2.

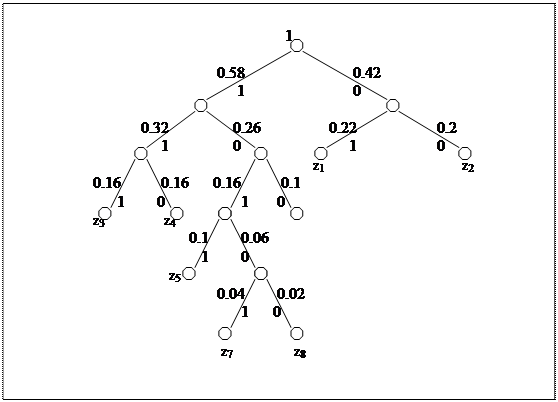
Рис. 5.2.

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:

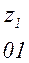
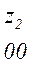
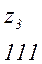
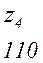
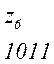
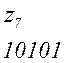
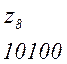
Задача построения кода Хаффмена может решатся непосредственно через построение кодового дерева по алгоритму 2:

Построение графа-дерева начинается с висячих вершин, которым в качестве весов назначают вероятности p(x_i), i = 1, …, r. Висячие вершины графа упорядочивают в соответствии с их весом. Это позволяет в дальнейшем уменьшить число пересечений ребер или вовсе исключить их.

Далее дерево строится по следующему алгоритму.

Шаг 1. Определяется число поддеревьев графа. Если оно меньше двух, то дерево построено и на этом действие алгоритма заканчивается. Если число поддеревьев равно или больше двух, то осуществляется переход к шагу 2. (Замечание. В начале построения имеется r изолированных вершин графа, являющихся поддеревьями и одновременно корнями поддеревьев.)

Шаг 2. Выбираются корни двух поддеревьев графа с минимальными весами и осуществляется сращение выбранных поддеревьев с добавлением при этом одной вершины и двух ребер. Вес вновь образованной вершины определяется как сумма весов корней выбранных поддеревьев, левому добавленному ребру приписывается вес, равный единице, правому – равный нулю. Далее переход к шагу 1.

В результате применения алгоритма образуется кодовое дерево-граф со взвешенными ребрами. Для получения кода сообщения x_i, достаточно выписать веса ребер, составляющих путь из корня дерева в соответствующую висячую вершину.

Проиллюстрируем метод Хаффмена построение кода по алгоритму 2.

Пример 5.5 Разработать код с использованием метода Хаффмена для входного алфавита x={x₁, x₂, …, x₈} и выходного алфавита B={0, 1}, если p(x₁)=0.19; p(x₂)=0.16; p(x₃)=0.16; p(x₄)=0.15; p(x₅)=0.12; p(x₆)=0.11; p(x₇)=0.09; p(x₈)=0.02, и определить коэффициент избыточности полученного кода.

Построим кодовое дерево (рис. 5.3) и в соответствии с ним составим кодовую таблицу, дополнив ее промежуточными вычислениями, необходимыми для определения коэффициента избыточности (табл. 5.7).

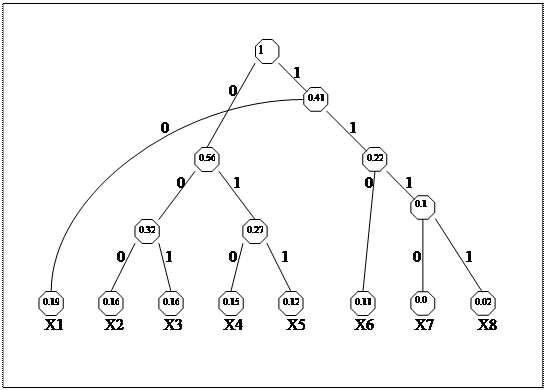
Рисунок 5.3.

Таблица 5.7

Знаки xi	Вероятности p(xi)	Кодовая комбинация	ni	ni p(xi)	p(xi)logp(xi)
x1	0.19	10	2	0.38	-0.45522
x2	0.16	000	3	0.48	-0.42301
x3	0.16	001	3	0.48	-0.42301
x4	0.15	010	3	0.45	-0.41054
x5	0.12	011	3	0.36	-0.36706
x6	0.11	110	3	0.33	-0.35028
x7	0.09	1110	4	0.36	-0.31265
x8	0.02	1111	4	0.08	-0.11288

Средняя длина кодовой комбинации

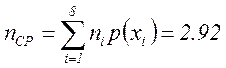(5.15)

Энтропия сообщения источника

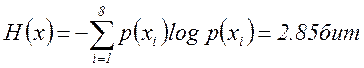(5.16)

Минимальная средняя длина кодовой комбинации определяется из равенства:

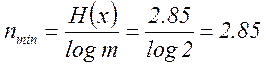(5.17)

Коэффициент избыточности

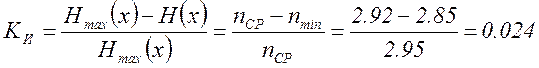(5.18)

Как видно из (5.18) построенный код практически не имеет избыточности.

5.4.2 Свойство префиксности эффективных кодов [1 и др.].

Рассмотрев методики построения эффективных кодов, нетрудно убедится в том, что эффект достигается благодаря присвоению более коротких комбинаций более вероятным знакам. Таким образом, эффект связан с различием в числе символов кодовых комбинаций. А это приводит к трудностям при декодировании. Конечно, для различия кодовых комбинаций можно ставить специальный разделительный символ, но при этом значительно снижается эффект, которого мы добивались, так как средняя длина кодовой комбинации по существу увеличивается на символ.

Более целесообразно обеспечить однозначное декодирование без введения дополнительных символов. Для этого эффективный код необходимо строить так, чтобы ни одна комбинация кода не совпадает с началом более длинной комбинации. Коды, удовлетворяющие этому условию, называют префиксными кодами. Последовательность 100000110110110100 комбинаций префиксного кода например кода

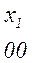
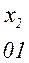
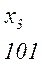
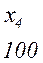
Декодируется однозначно

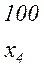
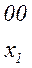
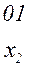
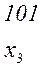
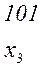
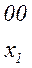
Последовательность 000101010101 комбинаций непрерывного кода, например кода

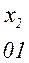
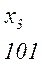
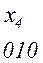
(комбинация 01 является началом комбинации 010) может быть декодирована по-разному:

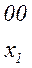
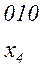
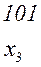
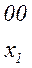
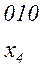
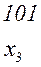
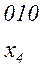
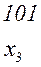
или

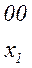
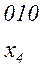
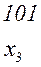
Нетрудно убедится, что коды, получаемые в результате применения методики Шеннона – Фано или Хаффмена, являются префиксными.

Дата добавления: 2014-12-07