
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Десятичные
|
|
|
|
Восьмеричные; 2) двоично-десятичные;
1) 28; 2) 11; 3) 13.
1) 19; 2) 9; 3) 11.
Десятичной; 2) троичной; 3) двоичной.
Меньше; 2) больше; 3) не изменяется.
Множитель, принимающий целочисленные значения.
Количество разрядов; 2) номер разряда;
Множитель, принимающий целочисленные значения.
Количество разрядов; 2) основание системы счисления;
Номер разряда.
Основание системы счисления; 2) количество разрядов;
4. Число Q, представленное в позиционной системе счисления, определяется по формуле:
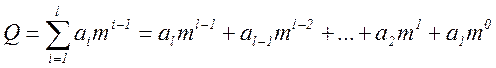
где  - представляет собой:
- представляет собой:
5. Число Q, представленное в позиционной системе счисления, определяется по формуле:

где 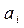 - представляет собой:
- представляет собой:
6. Число Q, представленное в позиционной системе счисления, определяется по формуле:
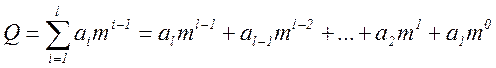
где чем больше основание  системы счисления, тем числом разрядов для представления данного числа Q требуется:
системы счисления, тем числом разрядов для представления данного числа Q требуется:
7. Физическая реализация соответствующих аппаратных средств, выполняющих логические и арифметические действия при преобразовании сообщений в цифру наиболее предпочтительная в системе счисления:
8. Наиболее удобно и просто арифметические и логические действия осуществлять в двоичной системе счисления.
Таблица сложения.
| 0 + 0 =? 0 + 1 =? 1 + 0 =? 1 + 1 =? | Правила сложения имеют решение | 1) 0 2) 1 3)0 1 0 1 1 0 1 0 10 10 |
9. Правила вычитания в двоичной системе счисления.
| 0 - 0 =? 0 - 1 =? 1 - 0 =? 1 - 1 =? | Имеет решение | 1) 0 2) 0 3)0 1 1 1 0 0 0 0 1 0 |
10. Наиболее распространенная при кодировании и декодировании логическая операция – сложение по модулю 2 – « ». В двоичной системе счисления таблица сложения по модулю 2 имеет вид:
». В двоичной системе счисления таблица сложения по модулю 2 имеет вид:
0 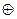 0 =?
0 0 =?
0 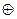 1 =?
1 1 =?
1 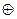 0 =?
1 0 =?
1 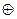 1 =? 1 =?
| Имеет решение | 1) 0 2) 0 3)1 1 1 1 1 1 0 1 0 1 |
11. Алгоритм перевода из двоичной системы счисления в привычную для человека десятичную систему счисления следующий: «Пересчет начинается со старшего разряда. Если в следующем разряде стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу». Найдите десятичный эквивалент двоичного числа 1001:
|
|
|
12. Алгоритм перевода из двоичной системы счисления в привычную для человека десятичную систему счисления следующий: «Пересчет начинается со старшего разряда. Если в следующем разряде стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу». Найдите десятичный эквивалент двоичного числа 1101:
13. Чтобы сохранить преимущества двоичной системы и удобство для человека десятичной системы при кодировании используют по наименованию промежуточные коды:
14. При программировании машинных логических и арифметических операций широко используются при кодировании как вспомогательная система счисления:
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 395; Нарушение авторских прав?; Мы поможем в написании вашей работы!