Совместной энтропией

Безусловной энтропией; 2) условной энтропией;

Сумма; 2) произведение; 3) разность.

1) 8; 2) 3; 3) 4.

Бод; 2) бит (двоичная цифра); 3) байт.

3. Неопределенность источника, приходящаяся на одно сообщение определяется по формуле Хартли:

(где p(x_i) – вероятность появления x_i -го сообщения) при p(x_i)= равна бит:

4. Энтропия H(x) как средняя мера неопределенности, приходящаяся на одно неравновероятное сообщение (независимые и несовместные) источника в соответствии с правилами теории вероятности определяется по формуле (p(x_i) – вероятности появления i-го сообщения источника):

1) 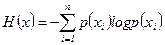; 2) ; 3) .

5. Энтропия ансамбля двух сообщений x₁ и x₂ (с априорной вероятностью p(x₁) = p и p(x₂) = 1 – p(x₁) = 1 – p) определяемая по формуле: достигает максимального значения H(x) = 1 бит при априорной вероятности p равной:

1) 0; 2) 1; 3) .

6. Энтропия источника равновероятных сообщений H₀(x)=logM=-logp(x) и неравновероятных сообщений (p(x_i) – вероятности появления i-го сообщения) между собой находится:

1) H₀(x) = H _i(x); 2) H₀(x) < H _i(x); 3) H₀(x) > H _i(x).

7. Энтропия двоичного источника с независимым выбором элементов, определяемой по формуле: H(x) = -plog₂p - (1-p)log₂(1-p) (здесь p – вероятность выбора одного элемента), при p = равна бит:

1) ; 2) 1; 3) .

8. Энтропия (если вероятность одного из состояний источника сообщений равна единица) равна бит:

1) 0; 2)1; 3) .

9. Энтропия объединения нескольких статистически независимых источников информации определяется как ________ энтропий источников:

10. Энтропия объединения двух зависимых сигналов {X, Y} определяется по формуле: H(X, Y) = H(X) + H(Y/X) = H(Y) + H(X/Y), где H(X/Y) или H(Y/X) называется:

11. Энтропия объединения двух зависимых сигналов {X, Y} определяется по формуле: H(X, Y) = H(X) + H(Y/X) (1).

В случае независимости сигналов X и Y формула энтропии объединения (1) примет вид:

1) H(X, Y) = H(X); 2) H(X, Y) = H(X) +H(Y);

3) H(X, Y) = H(Y) + H(X/Y).

12. Энтропия объединения двух зависимых сигналов {X, Y} определяется по формуле: H(X, Y) = H(X) + H(Y/X) (1).

В случае когда сигнал X принял значение x_K. При этом известно, что сигнал Y с необходимостью примет значение y_K. Формула энтропии объединения (1) примет вид:

1) H(X, Y) = H(X); 2) H(X, Y) = H(X) + H(Y);

3) H(X, Y) = H(X) + H(Y/X).

13. Совокупность устройств и физических сред, обеспечивающих передачу дискретных сообщений из одного места в другое называется:

Дата добавления: 2014-12-07