Дискретизация сигнала, при условии его восстановления методом интерполяции

Если функция x(t), удовлетворяющая условиям Дирихле и обладающая спектром с граничной частотой, дискретизирована циклически, с периодом, то она может быть восстановлена по этой совокупности ее мгновенных значений без погрешности. (сек) (Гц).

Представление сигнала посредством выборок. Теорема В.А.Котельникова

Как мы уже говорили, при оцифровывании сигнала делаются выборки, при этом, для получения значения сигнала применяют дискретизацию и квантование. В ряде случаев, моменты взятия выборок устанавливаются на оси времени случайно, при этом информация о форме сигнала теряется. По случайным выборкам мы можем определить только плотность распределения вероятностей. Таким образом, случайные выборки дают нам статистическую информацию о величине входного сигнала. Это означает, что таким способом мы можем измерить среднеквадратическое и пиковое значения входного сигнала, определить диапазон принимаемых им значений, но форму сигнала и его спектр мы определить не сможем.

Во многих случаях взятие выборок сигнала осуществляется в равноотстоящие моменты времени. Тогда важно решить вопрос о том, как много выборок надо брать в единицу времени, чтобы иметь возможность достаточно полно описать непрерывный по времени сигнал. Ответ на этот вопрос даёт теорема В.А.Котельникова. В иностранной технической литературе Вы можете столкнуться с другим названием этой теоремы, которая трактуется как теорема Шеннона о выборках.

В этой теореме утверждается, что для восстановления без ошибок исходного сигнала по его выборочным значениям, взятым через равные промежутки времени, частота взятия выборок должна более, чем вдвое превосходить частоту самой высокочастотной составляющей, присутствующей в непрерывном входном сигнале. Строго говоря, текст теоремы В.А.Котельникова звучит следующим образом:

Условие Дирихле означает, что функция ограничена, кусочно непрерывна и имеет ограниченное число экстремумов.

Особенностью сигнала, дискретизированного в соответствие с теоремой Котельникова является то, что он может быть восстановлен с помощью фильтра нижних частот. Следовательно, если дискретизированный с шагом 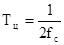сигнал х(t)дискр. подать на вход идеального фильтра с верхней границей пропускания 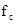, то на выходе получается восстановленный без погрешностей непрерывный сигнал х(t) (Рис)

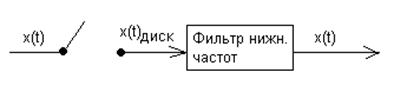
Рис.. Схема дискретизации и восстановления сигнала

Рассмотрим передачу нескольких сигналов по одной линии связи, для этого их необходимо дискретизировать. Эта операция реализуется с помощью коммутатора, затем информация передаётся по линии связи и далее, зная частоту работы коммутатора, мы можем восстановить её на другом конце линии связи (рис.). Частота опроса коммутатора должна быть 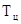n, где n — число измерительных преобразователей.

Теорема Котельникова позволяет производить преобразования аналогового сигнала в цифровой, необходимый для его дальнейшей обработки с помощью средств вычислительной техники. Выбор шага дискретизации по Котельникову гарантирует сохранность в дискретном представлении сигнала, всей информации о его спектральном составе. Для преобразования аналогового сигнала в цифровой используют АЦП. Частота дискретизации АЦП в соответствии с теоремой Котельникова 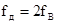, где — верхняя граничная частота сигнала.

Рис. Передача информации по одной линии связи

При обратном цифро-аналоговом преобразовании роль фильтра нижних частот выполняет микросхема ЦАП. Число разрядов АЦП и ЦАП преобразования определяют точность передачи амплитуды сигнала, т.к. определяют уровни дискретизации амплитуды сигнала. Таким образом, в компьютер поступает информация о сигнале в виде точек.

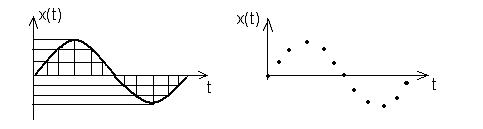
Рис. Дискретизация сигнала после АЦП

Обычно микросхемы АЦП выпускаются в одном корпусе с коммутаторами на n каналов. При этом в паспорте регламентируется частота опроса, которая может использоваться как для опроса n каналов, так и для опроса 1 канала. Ввод в компьютер информации производится через последовательный порт, например в стандарте RS-232.

В связи с этим проектант в каждом конкретном случае принимает решение об использовании нужной микросхемы с необходимым числом каналов, необходимой частотой опроса и числом разрядов АЦП преобразования.

Следует отметить, что дополнять измерительную схему фильтром нижних частот не всегда удобно, кроме того, наличие такого фильтра приводит к фазовым искажениям сигнала. От этих недостатков свободно восстановление сигнала методом простейшей интерполяции.

При этом методе полученные точки просто соединяются между собой отрезками прямых линий. Очевидно, что в этом случае плавные участки, близкие к прямым линиям, восстанавливаются с малыми погрешностями, а максимальная погрешность восстановления получается на участках с максимальной кривизной (рис.).

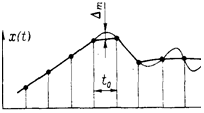Известно, что любую кривую x(t) на некотором участке можно разложить по степеням t, т. е. описать многочленом. В простейшем случае, используя лишь первые члены разложения, участок кривой между отсчетами можно представить в виде параболы, тогда погрешность линейной интерполяции будет представлять собой разность между этой параболой и ее хордой, соединяющей смежные отсчеты. Как известно, парабола имеет наибольшее отклонение от хорды в середине интервала интерполяции t₀ с абсолютным значением (D_m на рис.)

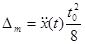
где 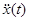- значение второй производной процесса х(t) т. е. оценка его кривизны. Отсюда максимальное значение погрешности восстановления наблюдается на участках кривой с наибольшей кривизной (в области максимумов и минимумов процесса предст. на рис.).

Если нас интересует не абсолютная погрешность D_m, а ее приведенное значение 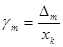, где x_k — предел измерений, то можно определить максимальный допустимый период дискретизации t_ц при котором погрешность восстановления не будет превышать g_m:

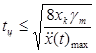
Так как любую сложную кривую можно разложить на ряд гармонических составляющих, то определим необходимый период дискретизации для синусоидального процесса. При x(t)=x_ksinwt оценка текущей кривизны 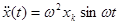, а ее максимальное значение 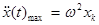. Отсюда необходимый период дискретизации для синусоидального процесса

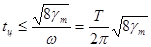(3)

Соотношение (3) воспринимается более наглядно, если его помощью вычислить число точек п, приходящихся на каждый период Т синусоидального процесса:

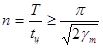(4)

Это соотношение дает:

gm	0,1
n

Таким образом, для восстановления синусоидального процесса с максимальной погрешностью 1 % при равномерной дискретизации необходимо иметь 22 отсчета на период процесса, но для представления с погрешностью 0,1% нужно не менее 70 отсчетов на каждый период, а для g_m =20% достаточно пяти отсчетов на период.

Исходя из соотношения (4), можно подсчитать минимальный период или максимальную частоту процесса, который может быть зарегистрирован с заданной максимальной погрешностью g_m. Данные о максимальных погрешностях при использовании некоторых приёмов и средств приведены в табл. и свидетельствуют о том, что без использования специальных средств могут быть зарегистрированы лишь очень медленные процессы (с периодом 0,2—2 с).

Метод регистрации	t0 с	Период или частота процесса при gm, % равной
0,1
Запись в журнал с показывающего прибора		7 мин.	2,2 мин.	42 с
Цифропечать	0,5	35 с	11 с	3,5 с
Перфоратор	0,027	1,9 с	0,6 с	0,2 с
АЦП с компьтером (условно)	30 ×10^-6	500 Гц	1,5 кГц	5 кГц

Выражая g_m из выражения (3) или (4) получаем

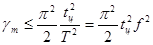(5)

т. е. динамическая погрешность восстановления g_m возрастает е квадратом частоты восстанавливаемого процесса.

На практике чаще всего приходится измерять существенно несинусоидальные процессы, содержащие гармонические составляющие или высокочастотные составляющие шумов, помех или наводок. В этих случаях динамическая погрешность восстановления процесса по дискретным отсчетам резко возрастает, о чем исследователь должен всегда помнить.

Рассмотрим это свойство погрешности восстановления на конкретном примере. Так, в табл. указано, что при использовании АЦП с периодом дискретизации t_ц =30 мкс исследуемый процесс с частотой f₁ =500 Гц восстанавливается с g_m1»0,1%. Действительно, рассчитывая g_m1 по формуле (5), получаем

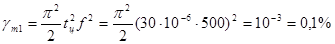
что часто можно считать достаточно высокой точностью восстановления. Однако если в кривой этого процесса содержится дополнительно еще 10-я гармоника с частотой f₁₀ =5000 Гц и амплитудой в 0,1 основной волны, она будет восстанавливаться с относительной погрешностью g_m10, в 100 раз большей, чем g_m1, т. е. равной 10%. Правда, так как амплитуда этой гармоники в 10 раз меньше амплитуды основной волны, то приведенное значение этой погрешности составит лишь g_m10 =1% • Тем не менее результирующая погрешность восстановления всего процесса будет в 10 раз (!) больше, чем погрешность восстановления g_m1 =0,1% процесса, не содержащего этой высокочастотной составляющей.

Погрешность восстановления для основной волны и ее гармоник является систематической (она всегда отрицательна, см. рис. и приводит к уменьшению восстанавливаемой амплитуды кривой), однако если высокочастотная составляющая вызвана шумом или другими помехами и не синхронна с основной волной, то и погрешность восстановления оказывается случайной и наблюдается в виде случайного разброса отсчетов.

При ручной регистрации наблюдений подобный разброс данных будет сразу замечен экспериментатором и он примет соответствующее решение о ходе эксперимента. Рассмотренное явление особенно опасно при автоматическом вводе данных в компьютер и подчеркивает крайнюю важность метрологического анализа динамических погрешностей в этом случае.

Однако в связи с постоянным увеличением быстродействия компьютеров этот способ дискретизации и восстановления становится очень привлекательным.

5.5 Фильтрация сигналов

Операция выделения из спектра сигнала определенной полосы частот называется фильтрацией. Фильтры подразделяются на фильтры низких частот (а), фильтры высоких частот (б) и полосовые фильтры (в).

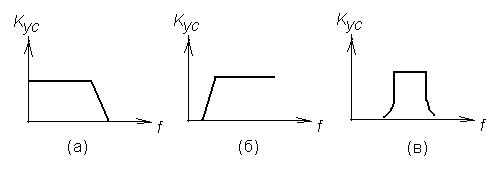
Рис. Виды фильтров.

Фильтры низких частот (а), фильтры высоких частот (б), полосовые фильтры (в)

Простейшие аналоговые фильтры состоят из R-C цепочек, для увеличения крутизны фильтры делают многозвенными.

Цифровая фильтрация заключается в том, что сигнал x(t) пропускают через математический фильтр, в котором реализуется требуемая характеристика.

5.6 Модуляция и детектирование

Воздействие измерительного сигнала x(t) на какой-либо стационарный сигнал называют модуляцией.

В качестве стационарного сигнала, называемого носителем, выбирают синусоидальное колебание

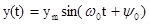(6)

и последовательность импульсов

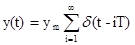
Выделение из модулированного сигнала составляющей, пропорциональной измеряемому сигналу, называется детектированием.

Синусоидальное колебание (6) определяется амплитудой , частотой 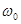, и фазой 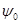. Все эти величины можно модулировать. В результате получаем амплитудную модуляцию АМ, частотную модуляцию ЧМ и фазовую модуляцию ФМ.

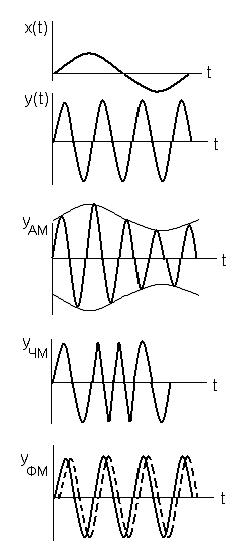
Рис. Виды модуляций

Модуляцию можно характеризовать как умножение модулируемой величины y(t) на множитель 1+mx(t), где х(t) — модулирующая функция такая, что 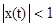, а m — глубина модуляции, причем 0<m<1.

При амплитудной модуляции

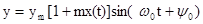
Если , выражение преобразуется

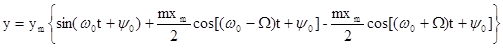
Отсюда следует, что модулированное колебание состоит из трех колебаний с частотами 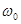, и .

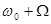Частота 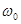называется несущей, а частота и 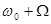боковыми частотами. Если модулирующий сигнал является периодической функцией.

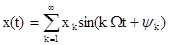
то модулированный сигнал у(t), будет

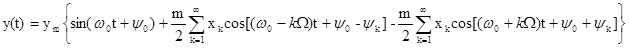
Видно, что модулированное колебание состоит из несущей частоты и двух групп, называемых боковыми полосами.

Для детектирования производят обратные манипуляции, разлагая функцию в ряд.

При частотной модуляции частота модулированного сигнала изменяется по закону

или, если 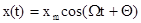, то

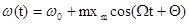(7)

Подставляя (7) в (6) и учитывая, что мгновенная фаза есть интеграл от частоты в выражении (6), получим

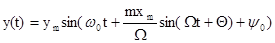
В этом выражении 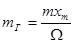— коэффициент частотной модуляции, зависящий от амплитуды модулирующего сигнала.

Представим это выражение в виде

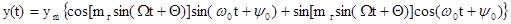(8)

При больших значениях коэффициента m_г это выражение является очень сложным и его можно выразить в виде рядов по функциям Бесселя. В целях упрощения предположим, что mг<<1, тогда

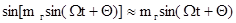
В связи с этим выражение (8) принимает вид

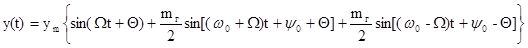(9)

Таким образом, при mг<<1 спектр частотно-модулированного сигнала не отличается от спектра АМС. Если условие mг<<1 не выполняется, т.е. имеет место глубокая частотная модуляция, то спектр модулированного сигнала будет содержать не две боковые частоты, а множество частот. Поэтому спектр ЧМ сигнала в общем случае больше спектра АМ сигнала.

Детектирование производится аналогично АМ сигналу.

При фазовой модуляции модулирующий сигнал воздействует на несущие колебания

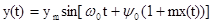
Если модулирующий сигнал 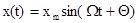, то

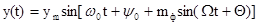(10)

где 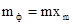— коэффициент фазовой модуляции, зависящий от амплитуды модулирующего сигнала.

В сигнале (10) информативным параметром является фаза 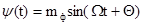, преобразуем сигнал (10)

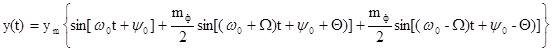
Сравнивая последнее выражение и выражение (9), можно сделать вывод, что сигналы ФМ и ЧМ совпадают. Различие же состоит в том, что коэффициент ЧМ зависит от частоты 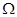модулирующего сигнала, тогда как коэффициент ФМ не зависит от частоты.

Это обстоятельство требует введения соответствующей коррекции сигнала после детектирования.

Детектирование производится аналогично АМ и ЧМ сигналам, при этом для получения фазы необходимо произвести интегрирование

Если в качестве модулируемого сигнала используется периодическая последовательность импульсов, то получим импульсную модуляцию (Рис.).

При этом имеем амплитудно-импульсную модуляцию (АИМ), частотно-импульсную модуляцию (ЧИМ), фазоимпульсную модуляцию (ФИМ) и широтно-импульсную модуляцию (ШИМ).

Если АМ, ЧМ, ФМ применяются в основном для аналоговых сигналов, хотя АМ применяется и для цифровых, то импульсные модуляции применяются в основном для цифровых сигналов.

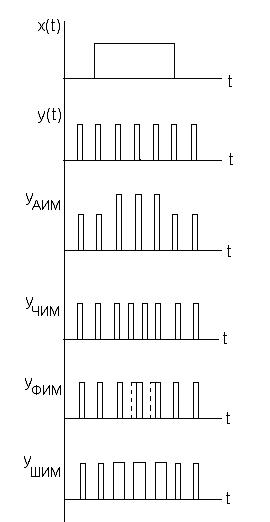
Рис. Импульсные виды модуляций

Дата добавления: 2014-12-07