Некоторые сведения из теории случайных функций

Как правило, при выполнении измерений динамических процессов мы имеем дело со случайными сигналами. К числу таких сигналов следует отнести все результаты измерений параметров движения таких объектов как корабль, самолёт, ракета, подв. лодка. Очевидно, что если мы проектируем аппаратуру, работающую на этих объектах, например системы управления антенной локатора или орудий, то возмущающие воздействия на неё носят случайный характер. Отметим и то, что вибрация различных механизмов, (мостов, станков, рельс и др.) также носит случайный характер. Таким образом целесообразно рассмотреть подробнее математический аппарат, используемый для описания случайных процессов.

Случайный процесс называют стационарным, если все моменты его распределения (мат. ожидание, дисперсия, СКО и т.д.) не изменяются при любом сдвиге начала отсчета вдоль оси времени.

С физической точки зрения это означает, что стационарный случайный процесс имеет место при таком режиме, когда все условия, определяющие протекание этого процесса, не изменяются с течением времени.

Например, в том случае, если морское волнение или вибрация станка являются установившемся, то есть не развивающемся и не затухающим то его можно принять стационарным.

Основные свойства случайной функции достаточно точно определяются математическим ожиданием и корреляционной функцией.

Следует отметить, что если математическое ожидание ординат процесса равно нулю, то такой процесс называется центрированным.

Таким образом, бортовая, килевая, вертикальная качка надводного корабля и рыскание есть центрированные процессы.

Если случайная функция является нормальной, т.е. она подчинена нормальному закону распределения то математическое ожидание и корреляционная функция полностью ее определяют.

Корреляционная функция стационарного случайного процесса 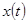зависит только от разности моментов времени 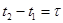для которых определяется корреляционная функция.

Рис. Стационарный случайный процесс

Если математическое ожидание случайного процесса 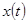равно нулю, то его корреляционная функция определяется соотношением:

(11)

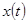Зная , можно определить еще одну важную характеристику колебаний. Эта характеристика называется спектральной плотностью случайной функции и характеризует распределение интенсивности колебаний по спектру частот.

Корреляционная функция и спектральная плотность стационарного случайного процесса связаны следующим соотношением:

(12)

Откуда можно получить выражение для через .

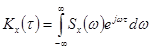(13)

Выражение (12) это прямое преобразование Фурье, а (13) обратное. Дисперсия 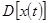случайной функции 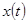, характеризующая интенсивность колебаний согласно (11) и (12) определяется выражением:

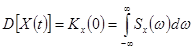(14)

Так как случайная функция характеризующая колебания, является вещественной, то вместо (12), (13), (14) и с учетом формул Эйлера можно получить следующие выражения:

зная дисперсию можно определить и среднее квадратическое значение углов качки:

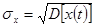
Корреляционная функция стационарного случайного процесса 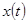с математическим ожиданием равным нулю, определяется соотношением (11). Однако для нахождения этой корреляционной функции нет необходимости обрабатывать реализации, полученные в результате наблюдения над многими процессами в однотипных условиях, например множество значений качки сделанных в разные промежутки времени, можно определить по единственно временной реализации случайного процесса 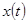, полученной в результате наблюдений над одним процессом в течение достаточно большого промежутка времени.

Это свойство стационарного случайного процесса называется эргодичностью.

Таким образом, математическое ожидание суммы нескольких отрезков реализации можно заменить математическим ожиданием длительной реализации.

Действительно, если мы возьмем записи качки судна за малое время, то будем иметь математические ожидания отличные от нуля. Их сумма даст нулевое значение. Аналогичное значение можно получить обработкой длительной по времени реализации, т.е.

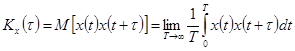
где М — символ. мат. ожидания; Т — интервал времени характеризующий всю кривую , при котором выполняется условие эргодичности.

Приближенно при достаточно большом времени реализации:

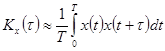(15)

Формула (15) и применяется при обработке реализации на компьютере с целью получения корреляционной функции процесса. При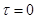

т.е. при значение корреляционной функции равно среднему значению квадрата случайной функции.

В том случае, если мы возьмем отношение 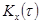и , то получим нормированную корреляционную функцию.

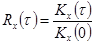
На рис. приведена нормированная корреляционная функция 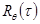случайного процесса.

Функция показывает, что действительно представляет случайную функцию, так как корреляционная связь между ординатами уменьшается с ростом . т.е. физический смысл корреляционной функции заключается в том, что она является мерой взаимной связи между значениям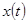и и для одной и той же реализации случайного процесса.

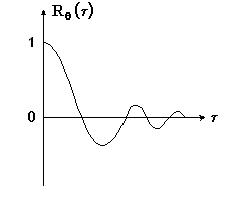
Рис.. Нормированная корреляционная функция 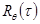например углов крена судна

В том случае, если нас интересует статистическая взаимосвязь двух стационарных случайных процессов, например ординат рыскания и килевой качки, то необходимо рассматривать взаимные корреляционные функции.

В общем случае выражения для взаимно корреляционных функций имеют вид:

В том случаи, если мы говорим о рыскании и килевой качке ; .

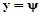Взаимная корреляционная функция характеризует связь двух разных случайных процессов между собой в различные моменты времени, отстоящие друг от друга на величину 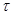. Если 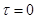то значения 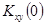характеризует эту связь в один и тот же момент времени. Для несвязанных друг с другом процессов при всех 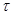значения .

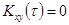Таким образом, следует запомнить,что корреляционной функцией стационарного случайного процесса называется среднее во времени значение за промежуток времени 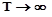от произведения случайных величин и взятых в случайном процессе в любые два момента времени и отличающихся друг от друга на определенный промежуток времени .

Как было сказано ранее выражение (12) и (13) связывают корреляционную функцию со спектральной плотностью.

Если имеются две случайные функции х(t) и y(t), то можно определить взаимные корреляционные функции и далее по формуле (13) можно найти взаимные спектральные плотности

В завершении рассмотрения вопроса следует отметить, что если ординаты процесса подчиняются нормальному закону распределения, то можно записать для них

Учитывая зависимость между дисперсией и средним квадратическим значением 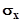случайного процесса, выражение может быть переписано

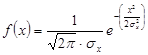где икс например .

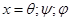Дата добавления: 2014-12-07