Основные понятия теории информации

Из теоремы Котельникова следует очень важный вывод о том, что передача всех значений сигнала не обязательна, если у него ограниченный спектр. Очевидно, что сигнал имеет ценность для получателя лишь тогда, когда он неизвестен получателю, т.е. несёт определенные новые сведения.

В 1928 году Хартли предложил определять количество информации J(x) в сообщении о некотором событии, как логарифм от функции, равной единице, деленной на вероятность появления этого события.

,

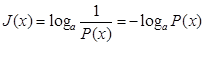где P(x)- вероятность наступления события x; а - основание логарифма

Так как 0<P(x) 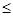1, то J(x)-величина всегда положительная.

Очень важно знать значение среднего количества информации на одно сообщение источника, которое математически совпадает с энтропией H(x). Понятие об энтропии введено К.Шенноном. Энтропия H(x)- это мера неопределённости исхода случайного опыта или события по определению Шеннона.

В измерительной технике под энтропией понимают меру, которая характеризует степень неопределенности системы. Источник информации, например датчик, может передать m сообщений x₁; x₂ … x_m с вероятностью нахождения источника в соответствующем состоянии P(x₁);P(x₂)…P(x_m), т.е. P(x_m) характеризует погрешность датчика или достоверность сообщения.

Количество информации и неопределенность для всей совокупности случайных сообщений можно получить усреднением.

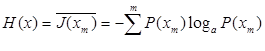
где 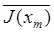- среднее на одно сообщение количества информации; Н(x)- мера недостатка информации о состоянии системы.

Единицы измерения энтропии и информации зависят от выбора основания логарифма. При использовании десятичных логарифмов энтропия измеряется в дитах, двоичных логарифмов, т.е. с основанием 2 – в битах, натуральных ln, т.е. с основанием е в нитах 1 нит= 1,44269 бит, 1 дит=3,32193 бит.

В связи с тем, что цифровая техника основана на передаче сигнала, шифрованного двумя состояниями потенциала, т.е. нулём и единицей в цифровой технике распространены биты.

Детальное и строгое исследование энтропии как меры неопределенности было проведено А.Я.Хинчиным. Он определил следующие свойства энтропии:

- Энтропия не может быть отрицательной величиной и для системы с конечным числом состояний всегда конечна;

- Энтропия равняется нулю, когда рассматриваемая система имеет достоверное событие;

- Энтропия имеет максимальное значение, если все события равновероятны;

- Энтропия объединённой системы равна сумме энтропий каждой из систем.

Отметим, что как, правило, измерительный или информационный сигнал отягощён шумом. Если на вход канала передачи информации подаётся сигнал с энтропией H(x), а шум в канале имеет энтропию 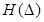, то количество информации на входе канала будет

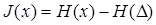
т.е. меньше энтропии передаваемого сигнала на величину энтропии шума.

Важной характеристикой передаваемых сигналов является избыточность. Если реальный сигнал для передачи определённого количества информации J(x) имеет n символов, а его передачу можно было произвести с минимально возможным числом символов n_min, то этот источник сообщений обладает избыточностью с коэффициентом избыточности

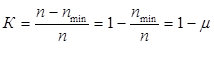
где 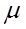- коэффициент сжатия.

Избыточность также определяют через энтропию источника сообщений

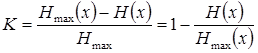
где H_max(x)- энтропия оптимального сообщения; H(x)- энтропия реального сообщения.

Для уменьшения избыточности необходимо увеличить энтропию сообщения. Избыточность увеличивает время передачи и повышает помехоустойчивость сообщений.

Во многих случаях информация о каком-либо явлении получается опосредованно, в результате наблюдения другого явления, связанного с первым. К таким случаям можно отнести многие измерения. Например, часто о местонахождении корабля или самолёта судят не по результатам непосредственного наблюдения, а по показаниям приборов.

Между местоположением корабля или самолёта и показаниями прибора существует определённая связь. Однако, наличие внешних помех, случайных, методических и аппаратных погрешностей нарушает однозначность связи между движущимся объектом и прибором, создавая некоторую неопределённость. Возникает вопрос, как определить количество информации о каком-либо явлении, если оно наблюдается не непосредственно, а через другой процесс. Для этой цели удобно воспользоваться понятием условной энтропии, которое характеризует неопределенность одного процесса по результатам наблюдения другого процесса. В данном случае количество информации о событии x, содержащемся в сообщении о событии y, определяется выражением

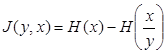
т.е. количество информации равно разности энтропии начального и конечного состояния системы. Причём энтропия конечного состояния системы х определяется не непосредственно, а через знание другой системы у, что и соответствует условной энтропии .

Последнее выражение для случая передачи сообщения может быть интерпретировано следующим образом: Н(х)- определяет среднее количество переданной информации, J(y,x)- среднее количество принятой информации, и условная энтропия является средним количеством информации, потерянной вследствие наличия помех.

Рассмотрим пропускную способность информационной системы.

В соответствии с теоремой Котельникова: если известно, что верхняя частота частотного диапазона канала F_max, то в каждую секунду должно передаваться 2F_max отсчетов. Количество информации в каждом отсчете, при равномерном распределении величины х в диапазоне 0-X_max и погрешности канала ±DX равно

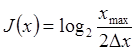
Пропускная способность

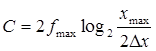
Для передачи информации с возможно меньшей ошибкой по каналу связи с помехами необходимо применять соответствующие методы кодирования. Пропускная способность канала при этом должна быть равна или больше того количества информации, которое передаётся.

Теоретически предельная скорость передачи информации или пропускная способность канала связи при наличии помех определяется согласно формуле Хартли-Шеннона

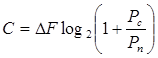
где 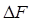- ширина полосы частот канала; Р_с - средняя мощность сигнала; Р_п - средняя мощность помех с нормальным законом распределения амплитуд.

Дата добавления: 2014-12-07