Частотные характеристики системы 2-го порядка

Определим параметры вынужденной составляющей при гармоническом воздействии x=Аsinwt. Комплексная передаточная функция системы 2-го порядка, найденная путем подстановки комплексной переменной преобразования Лапласа p = jw в передаточную функцию (22) будет:

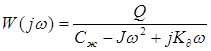. (30)

Модуль передаточной функции:

,

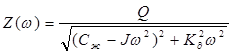при нулевой частоте 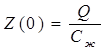. Разделив Z(w) на Z(0) получим выражение АЧХ системы второго порядка:

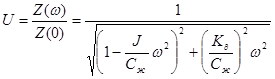
или с учетом того, что :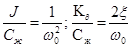

,

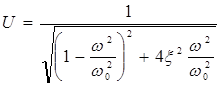Введем относительную частоту 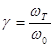, где w_Т – текущее (задаваемое при построении АЧХ) значение частоты. Тогда выражение для U примет вид:

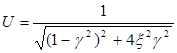. (31)

Фазо-частотная характеристика системы второго порядка следует из комплексной функции (30):

.

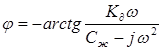или принимая во внимание ; 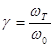, получим:

.

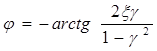Как указывалось ранее, наиболее простыми и часто встречающимися (типовыми) соединениями звеньев являются последовательное, параллельное и встречно-параллельное (охват звена обратной связью). При последовательном соединении звеньев выходная величина каждого из звеньев, кроме последнего служит входной величиной следующего звена. Эквивалентная передаточная функция последовательного соединения n звеньев равна произведению передаточных функций этих звеньев:

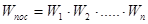
При параллельном соединении все звенья имеют одну и ту же входную величину, а их выходные величины суммируются. Передаточная функция параллельного соединения n звеньев равна сумме передаточных функций этих звеньев:

.

Встречно - параллельное соединение звеньев приводит к образованию замкнутой системы и состоит из двух звеньев. Звено с передаточной функцией W_п является прямой цепью передачи сигналов, а звено с передаточной функцией W_о осуществляет обратную связь. Если воздействие обратной связи совпадает по знаку с входной величиной, то обратная связь положительная, в противном случае отрицательная. Эквивалентная передаточная функция встречно – параллельного соединения

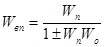
здесь знак + соответствует отрицательной обратной связи, а знак – положительной.

Эквивалентные передаточные функции при соединении звеньев различного типа рассмотрены в учебном пособии Макаров И.М., Менский Б.М. «Линейные автоматические системы». М. Машиностроение 1982 г.

10. Синтез динамических характеристик приборов.

10.1 Оптимизация параметров измерительной системы из условия минимума динамической погрешности

Погрешность передаточной функции прибора можно определить как

DW(p) = W(p) – W(0)

где W(p) – реальная передаточная функция, W(0) – идеальная передаточная функция

Разложение функции DW(p) в ряд по степеням p, который сходится для малых р (для медленных процессов), дает:

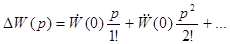
где есть дифференциалы W(p) по р.

Динамическая погрешность прибора обращается в нуль при выполнении условий оптимальности параметров прибора.

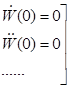
Число уравнений не может превышать числа независимых параметров, входящих в передаточную функцию, поэтому удовлетворить условиям оптимальности для всех членов ряда не представляется возможным.

Для систем второго порядка существуют точные решения, позволяющие оптимизировать параметры по различным критериям.

10.2 Оптимизация параметров измерительной системы второго порядка из условия минимума длительности переходного процесса.

Одним из важных критериев динамического качества является длительность переходного процесса, определяемая как время, начиная с которого кривая переходного процесса не выходит за границы допустимой динамической погрешности.

Обозначим относительное значение допустимой погрешности через

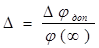
где Dj_доп – абсолютное значение допустимой погрешности.

При расчетах обычно допускают D = 0,05:-0,1. В области 0 < x < 1 существует оптимальное значение x, при котором длительность переходного процесса при выбранном значении w₀ будет наименьшей.

Представим уравнение (25) в безразмерной форме:

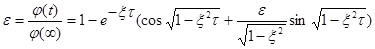(32)

График, построенный по уравнению (32) для трех близких значений x, показывает, что минимум безразмерной длительности переходного процесса будет при таком значении x=x₁, при котором максимум функции (32) после первого перехода через установившееся значения совпадает с верхней границей допустимой динамической ошибки 1+ D (кривая 1). Этой кривой соответствует длительность процесса t₁, при которой кривая 1 входит в зону допуска в точке А.

Допустим, что x₂ > x₁. Тогда период колебаний увеличится и переходный процесс будет описываться кривой 2, расположенной правее кривой 1 и входящей в зону 1± D в точке В, для которой t₂>t₁. Если же x₃<x₁ (кривая 3), то период колебаний уменьшится, но увеличится величина перехода через установившееся значение, из-за чего максимальное отклонение кривой 3 выйдет за пределы верхней границы допуска + D.

Рис К расчёту оптимальной степени успокоения по критерию минимума длительности переходного процесса

Длительность t₃ процесса будет определяться вторым пересечением кривой 3 с верхней границей зоны допусков в точке С (т.е в зону допуска кривая войдет в конце первого полупериода). Следовательно: t₃>t₁.

Таким образом, задача отыскания оптимального значения x сводится к определению такого его значения, при котором первый максимум функции равен 1+ D. Выражение для оптимального значения x можно найти, приравнивая в формуле (28) s=D.:

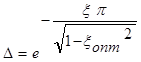
откуда оптимальная степень успокоения:

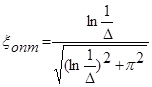(33)

Из последней формулы следует, что величина x_опт зависит от величины допуска D.

Подставляя (33) в (32) и приравнивая e =1-D получим уравнение, однозначно определяющее минимальную безразмерную длительность переходного процесса:

,

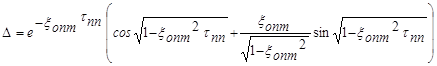это уравнение не имеет явного решения относительно t_nn, но может быть решено численно. Его численные решения, т.е. зависимость D (x_опт, t_пп) приведена в таблице:

D		± 0,025	± 0,05	± 0,1	± 0,25
xопт	1,0	0,76	0,69	0,59	0,404
tпп	¥	2,83	2,6	2,32	1,95

Действительная длительность процесса равна найденному из таблицы значению безразмерной длительности t_пп деленному на собственную частоту недемпфированных колебаний:

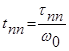(34)

Из формулы (34) следует, что длительность переходного процесса теоретически можно неограниченно уменьшать путем увеличения w₀, однако на практике возможности увеличения w₀ ограничены. Увеличение 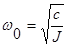в случае с маятниковым акселерометром возможно за счет увеличения С и уменьшения J. Если выбран тип чувствительного элемента и определены его размеры, исходя из получения максимального вращающего момента М_max, превышающего в нужное число раз вредные моменты, то при заданном максимальном угле j_max поворота подвижной системы, жесткость С определяется из условия равновесия системы в статическом режиме 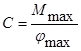. Что касается момента инерции J, то он складывается из двух составляющих:

J=J_чэ + J_пр ,

где J_чэ – момент инерции подвижной части чувствительного элемента; J_пр –приведенный момент инерции масс подсоединенных к подвижной части, т.е. передаточного механизма, стрелки якоря и т. д.

При выбранном типе и размерах чувствительного элемента величины J_чэ и М_max оказываются взаимосвязанными. Уменьшение J_чэ приведет к уменьшению M_{max .}. Остается возможность уменьшения J_пр за счет уменьшения масс механизмов подсоединенных к подвижной части. Но здесь также существует предел. Таким образом, в каждой конструкции существует практический максимум собственной частоты

,

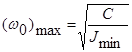следовательно, наименьшая практически достижимая длительность переходного процесса

.

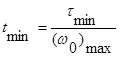После того как выбраны С, J, w₀ и x_опт нетрудно найти оптимальный коэффициент демпфирования:

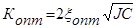
10.3 Оптимизация параметров прибора по критерию максимума ширины полосы пропускания частот

Анализ формулы (23) показывает, что существует оптимальное значение x, при котором полоса пропускания частот g_пр имеет максимум. Определим полосу пропускания частот, как диапазон частот, внутри которого отклонение амплитуды от 1 не превышает величины допустимой динамической ошибки ± D.

На графике представленном на рисунке, подтверждается, что максимум g_пр будет при таком значении x= x_1, при котором максимум функции U совпадает с верхней границей допусков 1+D (кривая 1). При этом полоса пропускания частот g₁, определяется абсциссой точки А, в которой кривая 1 выходит за пределы поля допуска. Допустим, что x₂>x₁, тогда АЧХ будет описываться кривой 2, расположенной ниже кривой 1 и выходящей из зоны допусков в точке В, для которой g₂<g₁. Если же x₃<x₁, то максимальное значение кривой 3 будет превышать верхнюю границу допусков и полоса пропускания частот будет определяться точкой С, для которой g₃<g_{1 .} Таким образом, задача отыскания оптимального x сводится к определению его значения, при котором максимум функции U равен 1+D. Обозначим через Z подкоренное выражение в формуле (31):

Рис.. К расчёту оптимальной степени успокоения по критерию максимума полосы пропускания частот

Очевидно, что максимум функции U будет при том же значении g, при котором функция Z имеет минимум. Это значение g можно определить, приравнивая нулю первую производную Z по g:

,

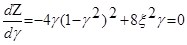откуда: g² = 1- 2x².

Подставляя найденное значение для g² в правую часть формулы (31) и приравнивая ее левую часть 1+ D, получим условие для определения оптимального x:

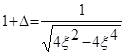или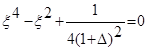

Решая биквадратное уравнение, находим оптимальное значение степени успокоения:

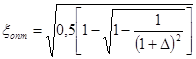(35)

Ширину полосы пропускания частот g_пр, отвечающую оптимальному значению x_опт, можно определить, подставляя в формулу (31) x= x_опт и приравнивая левую часть 1 -D:

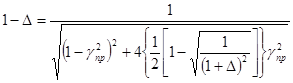
откуда:

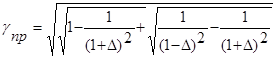(36)

по формулам (35) и (36) вычислены значения x_опт и g_пр для различных значений D.

D		±0,025	±0,05	±0,1	±0,25
xопт	0,707	0,626	0,590	0,540	0,447
gпр		0,737	0,876	1,04	1,31

Действительная полоса пропускания w_пр равна найденному из таблицы значению g_пр умноженному на собственную частоту недемпфированных колебаний: w_пр= g_прw_{0 .}

Следует отметить, что полоса пропускания датчика включает и рабочий диапазон частот и резонансную область.

Анализируя таблицы значений D, полученные при оптимизации по длительности переходного процесса и при оптимизации по максимуму полосы частот можно сделать вывод, что оптимизация по длительности переходного процесса уменьшает полосу пропускания при заданной динамической погрешности D. Однако если прибор работает в режимах, при которых возможны частые переходные процессы, т.е. прибор измеряет нестационарные процессы, то с целью уменьшения динамической погрешности есть смысл жертвовать полосой пропускания частот.

Дата добавления: 2014-12-07