
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изоморфизм частично упорядоченных множеств
|
|
|
|
Частично упорядоченные множества 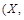 p) и (Y, p ¢) изоморфны, если чуществует биекция
p) и (Y, p ¢) изоморфны, если чуществует биекция 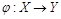 , сохраняющая отношение порядка, т.е.
, сохраняющая отношение порядка, т.е. 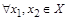 таких, что
таких, что  p
p 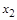 , выполняется
, выполняется 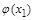 p ¢
p ¢ 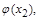
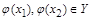 .
.
Пример. Рассмотрим множество T точек горизонтальной прямой, упорядоченное отношением L – “лежит левее или совпадает”, и множество действительных чисел R с введенным на нем отношением порядка “£”. Тогда (T, L) изоморфно (R, £) и, решив задачу на множестве R, мы иллюстрируем решение с помощью множества T, так как структура этих множеств одинакова.
Теорема. Всякое частично упорядоченное множество изоморфно некоторому подмножеству его булеана, упорядоченному отношением включения.
Пример. Рассмотрим частично упорядоченное множество (X, ½) из 1.2.7. Так как 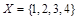 состоит из
состоит из 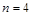 элементов, то его булеан B (X) содержит
элементов, то его булеан B (X) содержит 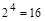 элементов – подмножеств множества X. Выберем из них 4 подмножества следующим образом: сопоставим каждому элементу
элементов – подмножеств множества X. Выберем из них 4 подмножества следующим образом: сопоставим каждому элементу 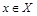 подмножество
подмножество  B (X), включающее те и только те элементы y, которые являются делителями элемента x:
B (X), включающее те и только те элементы y, которые являются делителями элемента x:
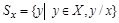 .
.
Получим множество  B (X), где
B (X), где  ,
, 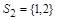 ,
, 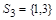 ,
,  . Частично упорядоченные множества (X, ½) и (
. Частично упорядоченные множества (X, ½) и (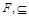 ) изоморфны (рис. 1.10).
) изоморфны (рис. 1.10).
 |
Доказательство теоремы. Пусть задано произвольное упорядоченное множество 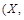 p). Построим подмножество
p). Построим подмножество 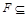 B (X) с помощью соответствия: каждому элементу
B (X) с помощью соответствия: каждому элементу 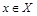 сопоставим
сопоставим 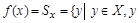 p x } и обозначим
p x } и обозначим 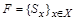 .
.
Покажем, что соответствие 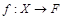 является биекцией, т.е. выполняются условия а – г определения биекции из 1.2.1. Условия а – в выполняются согласно способу построения множества F: каждый элемент
является биекцией, т.е. выполняются условия а – г определения биекции из 1.2.1. Условия а – в выполняются согласно способу построения множества F: каждый элемент 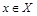 имеет единственный прообраз
имеет единственный прообраз 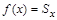 , а каждый элемент
, а каждый элемент 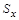 множества F имеет прообраз
множества F имеет прообраз 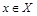 . Покажем, что этот прообраз – единственный. Предположим противное: существует два различных элемента
. Покажем, что этот прообраз – единственный. Предположим противное: существует два различных элемента 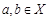 , имеющие одинаковые прообразы
, имеющие одинаковые прообразы 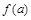 и
и 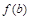 , т.е.
, т.е. 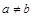 , но
, но  .
.
В силу рефлексивности отношения порядка “ p ” имеем:
a p a  p b.
p b.
Аналогично,
b p b  p a.
p a.
Так как отношение порядка антисимметрично, получим 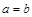 , что противоречит нашему предположению. Следовательно, различные элементы
, что противоречит нашему предположению. Следовательно, различные элементы 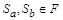 имеют различные прообразы:
имеют различные прообразы: 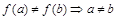 , а отображение
, а отображение 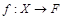 является биекцией.
является биекцией.
Докажем, что биекция 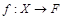 сохраняет порядок, т.е. если
сохраняет порядок, т.е. если 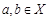 и a p b, то
и a p b, то 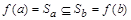 . Согласно определению включения множеств достаточно показать, что
. Согласно определению включения множеств достаточно показать, что 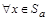 выполняется
выполняется 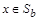 .
.
Возьмем произвольный элемент 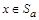 . Тогда x p a, но a p b, поэтому x p b (в силу транзитивности отношения порядка) и
. Тогда x p a, но a p b, поэтому x p b (в силу транзитивности отношения порядка) и 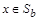 . Доказано включение
. Доказано включение  .
.
Итак, построенное отображение 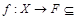 B (X) является биекцией, сохраняющей отношение порядка. Следовательно, частично упорядоченные множества (X, ½) и (
B (X) является биекцией, сохраняющей отношение порядка. Следовательно, частично упорядоченные множества (X, ½) и (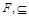 ) изоморфны. Теорема доказана.
) изоморфны. Теорема доказана.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1198; Нарушение авторских прав?; Мы поможем в написании вашей работы!