
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства бинарных отношений
|
|
|
|
Способы задания бинарного отношения
Определение бинарного отношения
Определение. Говорят, что на множестве X задано бинарное отношение R, если задано подмножество декартова произведения  (т.е.
(т.е. 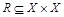 ).
).
Пример 2. Пусть  Зададим на Х следующие отношения:
Зададим на Х следующие отношения:
 – отношение равенства;
– отношение равенства;
 – отношение предшествования;
– отношение предшествования;
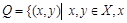 делится на
делится на  – отношение делимости.
– отношение делимости.
Все эти отношения заданы с помощью характеристического свойства. Ниже перечислены элементы этих отношений:
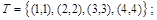


Тот факт, что пара (x, y) принадлежит данному отношению R,будем записывать: 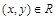 или xRy. Например, для отношения Q запись 4 Q 2 означает, что 4делится на 2 нацело, т.е.
или xRy. Например, для отношения Q запись 4 Q 2 означает, что 4делится на 2 нацело, т.е. 
Областью определения  бинарного отношения R называется мно-жество
бинарного отношения R называется мно-жество 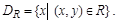
Областью значений  называется множество
называется множество 
Так, для отношения Р из примера 2 областью определения является множество 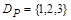 , а областью значений –
, а областью значений – 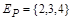 .
.
Бинарное отношение можно задать, указав характеристическое свойство или перечислив все его элементы. Существуют и более наглядные способы задания бинарного отношения: график отношения, схема отношения, граф отношения, матрица отношения.
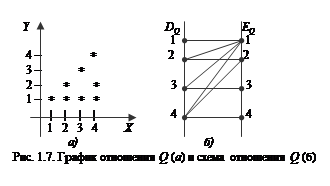
График отношения изображается в декартовой системе координат; на горизонтальной оси отмечается область определения, на вертикальной – область значений отношения; элементу отношения (х,у) соответствует точка плоскости с этими координатами. На рис. 1.7, а приведен график отношения Q примера 2.
Схема отношения изображается с помощью двух вертикальных прямых, левая из которых соответствует области определения отношения, а правая – множеству значений отношения. Если элемент (х,у) принадлежит отношению R, то соответствующие точки из  и
и  соединяются прямой. На рис. 1.7, б приведена схема отношения Q из примера 2.
соединяются прямой. На рис. 1.7, б приведена схема отношения Q из примера 2.
 |
Граф отношения 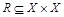 строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества Х. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х,у) принадлежит отношению R. На рис. 1.8, а приведен граф отношения Q примера 2.
строится следующим образом. На плоскости в произвольном порядке изображаются точки – элементы множества Х. Пара точек х и у соединяется дугой (линией со стрелкой) тогда и только тогда, когда пара (х,у) принадлежит отношению R. На рис. 1.8, а приведен граф отношения Q примера 2.
Матрица отношения 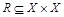 – это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества Х. На пересечении строки х и столбца у ставится 1, если пара
– это квадратная таблица, каждая строка и столбец которой соответствует некоторому элементу множества Х. На пересечении строки х и столбца у ставится 1, если пара 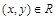 ; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй - номеру столбца. Пусть
; все остальные элементы матрицы заполняются нулями. Элементы матрицы нумеруются двумя индексами, первый равен номеру строки, второй - номеру столбца. Пусть  . Тогда матрица отношения
. Тогда матрица отношения 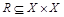 имеет n строк и n столбцов, а ее элемент
имеет n строк и n столбцов, а ее элемент  определяется по правилу:
определяется по правилу:

На рис.1.8, б приведена матрица отношения Q примера 2.
 |
Бинарные отношения делятся на типы в зависимости от свойств, которыми они обладают. Рассмотрим следующие отношения на множестве 
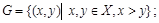

 делится на
делится на 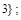

Отношение R на множестве Х называется рефлексивным, если для всех 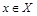 выполняется условие
выполняется условие  . Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство
. Среди приведенных выше отношений рефлексивными являются отношение L (т.к. неравенство  справедливо при всех
справедливо при всех 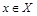 ) и отношение М (т.к. разность
) и отношение М (т.к. разность  делится на 3, значит, пара
делится на 3, значит, пара  принадлежит отношению М при всех
принадлежит отношению М при всех 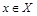 ).
).
Отношение R на множестве Х называется антирефлексивным, если условие  не выполняется ни при одном
не выполняется ни при одном 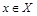 . Примером антирефлексивного отношения является отношение G (неравенство
. Примером антирефлексивного отношения является отношение G (неравенство  не выполняется ни при каких значениях х, следовательно, ни одна пара
не выполняется ни при каких значениях х, следовательно, ни одна пара  не принадлежит отношению G). Отметим, что отношение К не является рефлексивным
не принадлежит отношению G). Отметим, что отношение К не является рефлексивным  и не является антирефлексивным
и не является антирефлексивным 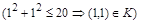 .
.
Отношение R на множестве Х называется симметричным, если из условия 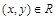 следует
следует  . Симметричными являются отношения М (если
. Симметричными являются отношения М (если  делится на 3, то и
делится на 3, то и  делится на 3) и К (если
делится на 3) и К (если  , то и
, то и  ).
).
Отношение R на множестве Х называется несимметричным, если для любых  из условия
из условия 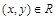 следует
следует  . Несимметричным является отношение G, т.к. условия
. Несимметричным является отношение G, т.к. условия  и
и  не могут выполняться одновременно (только одна из пар
не могут выполняться одновременно (только одна из пар 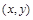 или
или  принадлежит отношению G).
принадлежит отношению G).
Отношение R на множестве Х называется антисимметричным, если для любых  из условия
из условия 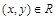 и
и  следует
следует 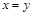 . Антисимметричным является отношение L, т.к. из одновременного выполнения
. Антисимметричным является отношение L, т.к. из одновременного выполнения 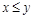 и
и  следует
следует 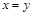 .
.
Отношение R на множестве Х называется транзитивным, если для любых 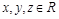 из одновременного выполнения условий
из одновременного выполнения условий 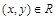 и
и 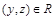 следует
следует  . Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если
. Отношения G, L, M являются транзитивными, а отношение К нетранзитивно: если 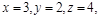 то
то  и
и  , но
, но 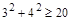 , то есть выполняются условия
, то есть выполняются условия  и
и  , но
, но  .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1141; Нарушение авторских прав?; Мы поможем в написании вашей работы!