Применение отношений для обработки данных

Отношение может быть не только бинарным, в общем случае отношением называется подмножество , т.е. элементом отношения является упорядоченный набор , где . При обработке данных наборы из n элементов называют записями, i -му элементу набора соответствует i -ое поле записи. Записи группируются в файлы, и если файлы содержат совокупность записей, удовлетворяющих некоторым отношениям, мы получаем базу данных. Таким образом, отношение удобно представлять в виде таблицы, каждая строка которой соответствует записи, а каждый столбец – определенному полю записи.

Любая ли таблица может задавать отношение? Очевидными являются следующие требования:

1) порядок столбцов таблицы фиксирован;

2) каждый столбец имеет название;

3) порядок строк таблицы произволен;

4) в таблице нет одинаковых строк.

Число n столбцов таблицы называется степенью отношения (говорят, что задано n -арное отношение). Число строк в таблице – количество элементов отношения. Математическая модель, описывающая работу с такими таблицами, называется реляционной алгеброй.

1.3.2. Теоретико-множественные операции реляционной алгебры

Так как отношения являются множествами, к ним применимы обычные операции теории множеств: пересечение, объединение, разность. Но в отличие от алгебры множеств в реляционной алгебре эти операции могут быть применены не к любым, а только к совместимым отношениям. Два отношения будем называть совместимыми, если их степени равны, а соответствующие поля относятся к однотипным множествам. Первое требование означает, что объединение, пересечение и разность определяются только для таблиц с одинаковым количеством столбцов, а второе – в соответствующих столбцах должны располагаться однотипные данные (не выполняется операция пересечения множества фамилий и множества зарплат).

Пересечением двух отношений R и S называется множество 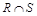всех записей, каждая из которых принадлежит как R, так и S (рис. 1.14, а, б).

Объединением двух отношений R и S называется множество записей, которые принадлежат хотя бы одному из отношений R или S (рис.1.14, а, в).

Разностью двух отношений R и S называется множество 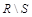всех записей, каждая из которых принадлежит отношению R, но не принадлежит отношению S (рис.1.14, а, г).

R				S
A1	A2	A3		B1	B2	B3
a	b	a		a	b	c
b	a	c
b	c	a		b	c	a

а)

R Ç S		R È S		R \ S
C1	C2	C2	D1	D2	D3	E1	E2	E3
b	c	a	a	b	a	a	b	a
			b	a	c	b	a	c
			b	c	a
			a	b	c

б) в) г)

Рис. 1.14. Операции над совместимыми отношениями

а) данные отношения R и S;

б) пересечение отношений R и S;

в) объединение отношений R и S;

г) разность отношений R и S

В реляционной алгебре вводится операция расширенного декартова произведения. Пусть – элемент n- арного отношения R, а 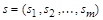– элемент m -арного отношения S. Конкатенацией записей r и s назовем запись 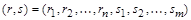, полученную приписыванием записи s к концу записи r.

R		S		R ´ S
A1	A2		B1	B2	B3		C1	C2	C3	C4	C5
a	b		k	l	m		a	b	k	l	m
a	c		b	k	c		a	b	b	k	c
c	e						a	c	k	l	m
							a	c	b	k	c
							c	e	k	l	m
							c	e	b	k	c

Рис. 1.15. Расширенное декартово произведение

отношений R и S

Расширенным декартовым произведением отношений R и S называется множество , элементами которого являются все возможные конкатенации записей и . Отметим, что полученное отношение имеет степень и важен порядок выполнения операции: .

В качестве упражнения запишите расширенное декартово произведение для отношений R и S (рис. 1.15) и сравните с отношением .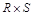

Дата добавления: 2014-12-07