Свойства конечных множеств

Классы равномощных множеств

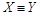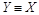Введенное в 1.4.1 отношение равномощности является отношением эквивалентности “ º “. В самом деле, оно рефлексивно: для каждого множества Х справедливо (Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y, то обратное отображение также является биекцией (если , то ). 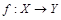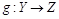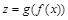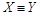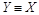Отношение транзитивно: если существует биекция и существует биекция , то соответствие отображает X на Z биективно (если и , то ).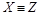

По свойству отношения эквивалентности (см. 1.2.5) получаем разбиение всех множеств на непересекающиеся классы равномощных множеств. Каждому классу присвоим название - кардинальное число. Таким образом, кардинальное число – это то общее, что есть у всех равномощных множеств. Обозначим кардинальное число множества 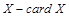или ½ Х ½. Пустое множество имеет кардинальное число Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества.

1.4.3. Сравнение множеств по мощности

Расположим классы эквивалентности равномощных множеств в порядке возрастания кардинальных чисел: .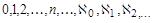

Для конечных множеств это не вызывает затруднений: 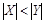означает для конечных множеств, что количество элементов множества X меньше количества элементов множества Y, и класс ½ X ½ расположен левее класса ½ Y ½ в последовательности классов равномощных множеств. А что означает неравенство ½ X ½<½ Y ½ для бесконечных множеств? Договоримся о следующих обозначениях:

1) если множества X и Y попадают в один класс эквивалентности, пишем ½ X ½=½ Y ½;

2) если класс эквивалентности множества X находится левее класса эквивалентности Y в ряду кардинальных чисел, используем обозначение ½ X ½<½ Y ½;

3) если класс эквивалентности множества X находится правее класса эквивалентности множества Y, то ½ X ½>½ Y ½;

4) в теории множеств строго доказано, что случай, когда множества X и Y несравнимы по мощности, невозможен – это означает, что классы равномощных множеств можно вытянуть в цепочку без разветвлений по возрастанию мощности.

Следующая теорема, приведенная без доказательства, позволяет устанавливать равномощность бесконечных множеств.

Теорема Кантора-Бернштейна. Пусть X и Y два бесконечных множества. Если во множестве X есть подмножество, равномощное множеству Y, а во множестве Y есть подмножество, равномощное X, то множества X и Y равномощны.

Пример. Пусть . Покажем, что ½ X ½=½ Y ½. Непосредственно биекцию X на Y построить трудно, т.к. X - отрезок с включенными концами, а Y – открытый интервал.

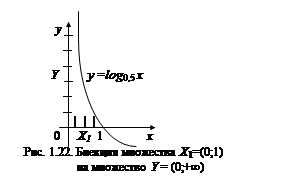Применим теорему Кантора-Бернштейна. Возьмем в качестве подмножества 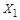множества X открытый интервал: 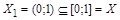. Биекция 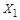на Y легко устанавливается: например, по закону 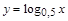(рис. 1.22), осуществляется взаимно однозначное отображение интервала (0;1) на интервал .

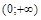В качестве подмножества возьмем любой замкнутый интервал из Y, например, 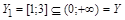. В 1.4.1 уже показано, что ½[1;3]½=½[0;1]½ (существует биекция 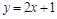). Таким образом, условия теоремы Кантора-Бернштейна выполняются, следовательно, множества 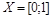и 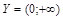равномощны (½ X ½=½ Y ½).

Множество X называется конечным, если существует биекция 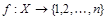, т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1,2,…, n }; при этом ½ X ½= n.

Все множества, для которых такую биекцию установить невозможно, будем называть бесконечными.

Пустое множество принято относить к конечным множествам и обозначать ½Æ½=0.

Сформулируем свойства конечных множеств в виде теорем (не все теоремы будут строго доказаны).

Теорема (правило суммы). Пусть множество X является объединением r непересекающихся конечных множеств 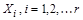. Тогда .

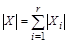Согласно условию теоремы система множеств 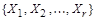является разбиением множества X. Доказательство проведем методом математической индукции по числу r блоков разбиения.

Шаг 1. Покажем, что теорема справедлива при 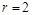. Пусть 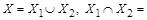Æи множества 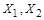конечны, т.е. существует биекция и 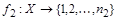. Установим биекцию 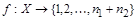следующим образом: всем элементам множества 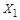оставим прежние номера, а номера элементов множества 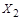увеличим на число 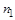. Полученное отображение

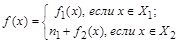
является биекцией 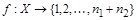в силу биективности и 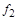. Следовательно, 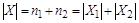. Основание индукции доказано.

Шаг 2. Индукционный переход заключается в следующем: предположим, что теорема справедлива при числе блоков разбиения 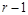; докажем, что в этом случае она будет справедлива и при числе блоков r.

Предположение: множества 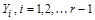, конечны и образуют разбиение множества Y. Тогда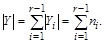

Рассмотрим разбиение множества X на r конечных множеств. Тогда 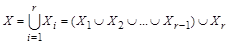по закону ассоциативности объединения. Обозначим 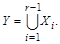Опираясь на основание индукции (шаг 1), имеем 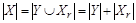, а по индукционному предположению 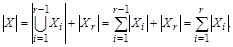Индукционный переход доказан.

Заключение. Согласно методу математической индукции, теорема справедлива для любого натурального числа r блоков разбиения.

Теорема (правило произведения). Пусть конечное множество X представлено в виде декартова произведения r конечных множеств 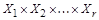. Тогда .

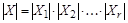Правило произведения доказывается методом математической индукции аналогично правилу суммы.

Теорема (о мощности булеана конечного множества). Пусть множество X конечно и 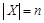. Тогда .

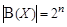Напомним, что B (X) есть булеан множества X, т.е. множество всех подмножеств множества X. При построении булеана в 1.1.8 мы использовали эту теорему без доказательства.

Доказательство. Множество X конечно, значит, существует биекция 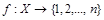. Зафиксируем порядок элементов множества 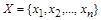и рассмотрим множество V всех упорядоченных наборов длины n, состоящих из нулей и единиц:

.

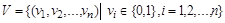Установим взаимно однозначное соответствие (биекцию) 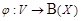следующим образом: элементу 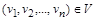сопоставляем множество 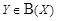, содержащее те и только те элементы 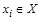, для которых 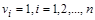. Легко проверить, что данное соответствие является биекцией. Таким образом, множество V и 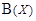равномощны. Но множество V является декартовым произведением n одинаковых сомножителей 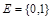, т.е. 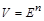и по теореме о мощности произведения 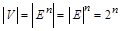, следовательно, и .

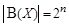Теорема (правило включения – исключения). Пусть 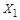и 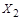конечные множества. Тогда .

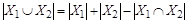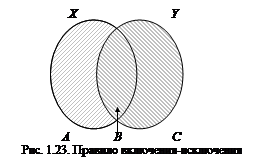
Доказательство теоремы опирается на правило суммы. Представим множество в виде объединения непересекающихся множеств 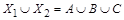, где 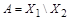, , 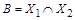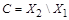(рис. 1.23). Тогда по правилу суммы 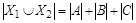, но 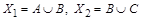, поэтому 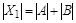, 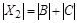. Имеем 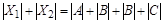, отсюда

.

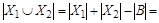
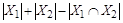Теорема (обобщенное правило включения – исключения).

Пусть конечное множество X является объединением r конечных множеств: Тогда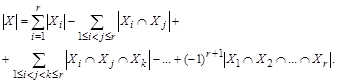

Теорема доказывается методом математической индукции по числу r блоков покрытия множества X.

Дата добавления: 2014-12-07