Решение задач 8,9 контрольной работы 1

Булеан бесконечного множества. Выводы

Мы показали, что несчетные множества имеют мощность большую, чем счетные. А существуют ли множества наибольшей мощности? На этот вопрос отвечает теорема, на основании которой мы можем утверждать, что не существует множества наибольшей мощности: для каждого множества X мы можем построить его булеан, т.е. множество большей мощности. Это означает, что ряд мощностей (рис. 1.25) неограничен.

Теорема. Пусть X – бесконечное множество. Мощность булеана множества X больше мощности множества X.

Доказательство. Очевидно, что мощность булеана B (X) не меньше мощности множества X: булеан имеет подмножество одноэлементных множеств, равномощное множеству X. Остается показать, что .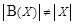

Предположим противное: пусть 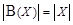. Это означает, что существует биекция , т.е. каждый элемент x множества X имеет единственный прообраз 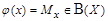, а каждый элемент булеана имеет единственный прообраз во множестве X. Рассмотрим множество 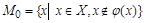. Покажем, что множество хотя и принадлежит булеану 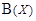, но не имеет прообраза 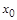во множестве X.

Действительно, пусть такой элемент 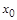существует, т.е. 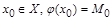. Тогда возможны два варианта: а) 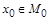, б) .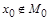

Случай а) невозможен, т.к. 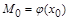и 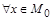выполняется 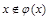, следовательно, 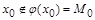. Аналогично невозможен и случай б): 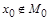, значит, 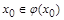, но 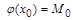. Полученное противоречие показывает, что не существует элемента , являющегося прообразом множества .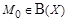

Следовательно, предположение о равномощности множеств X и 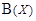неверно и остается принять .

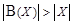Итак, используя понятие “мощность”, мы сравниваем между собой не только конечные, но и бесконечные множества. Мощность – это то общее, что есть у всех равномощных множеств, а общим у них является класс эквивалентности. Мы говорим, что множество имеет мощность À₀, и это означает, что оно принадлежит тому же классу эквивалентности, что и множество натуральных чисел; мы говорим, что множество имеет мощность континуума, и это означает, что оно принадлежит тому же классу, что и отрезок [0;1] (табл. 1.5). Другие классы бесконечных множеств используются реже, чем счетные и несчетные.

Таблица 1.5

Мощность множества

Множество	Эталон	Мощность
Конечное	{1, 2, …,n}	n
Счетное	N	À0
Несчетное	[0;1]	À

Задача 8. Даны множества 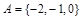и 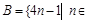N}. Какова мощность множеств ?

Решение. Множество A конечно и задано перечислением своих элементов, множество B задано характеристическим свойством. Запишем несколько первых элементов множества . Видим, что 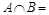Æ и 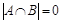, т.е. множество 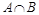конечно.

Покажем, что множество 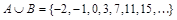счетно. Зану-меруем его элементы:

Задана биекция множества N на множество 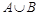, следовательно, 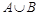счетно и .

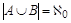По определению декартова произведения 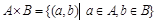. Запишем элементы этого множества в виде матрицы (рис. 1.27) и занумеруем их по столбцам.

A ¯ B ®					…
-2	(-2,3)1	(-2,7)4	(-2.11)7	(-2,15)10	…
-1	(-1,3)2	(-1,7)5	(-1,11)8	(-1,15)11	…
	(0,3)3	(0,7)6	(0,11)9	(0,15)12	…

Рис. 1.27. Множество A ´ B

Замечаем, что если номер n делится на 3 без остатка, то первый элемент пары равен 0; если номер n делится на 3 с остатком 1, то первый элемент пары равен –2; если номер n делится на 3 с остатком 2, то первый элемент пары равен -1. Поэтому способ нумерации может быть задан следующим образом:

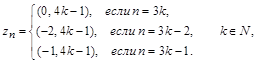
и множество 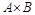счетно, т.е. имеет мощность À₀.

Задача 9. Равномощны ли множества 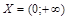и ?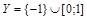

Решение. Покажем, что множества равномощны по теореме Кантора-Бернштейна, т.е. покажем, что найдется 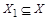такое, что , и найдется такое, что .

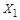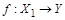Выберем в качестве множество и установим биекцию следующим образом:

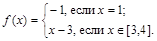
Множества 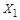и Y равномощны.

Пусть 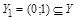. Установим биекцию 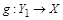по закону 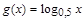. Множества 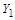и X равномощны. По теореме Кантора-Бернштейна .

Дата добавления: 2014-12-07