Правило шести точек

В пространстве любое твердое тело имеет шесть степеней свободы (3 перемещения и 3 вращения). Для того, чтобы придать телу необходимое определённое положение (позиционирование) относительно выбранной системы координат, необходимо и достаточно лишить шести степеней свободы, наложив на него шесть двусторонних геометрических связей. Такую связь условно можно представить в виде абсолютно жёсткого (недеформируемого) стержня между точкой твёрдого тела и координатной плоскостью, который неразрывно связан с телом и координатной плоскостью, но в то же время может скользить по ней, не теряя контакта. Примером двусторонней связи может служить связь абсолютно гладкого шара, расположенного между двумя абсолютно гладкими плоскостями (при отсутствии сил трения в точке контакта шара с этими плоскостями, см. рис. 4.2). Как видно из рисунка контакт точек А и В с плоскостями исключает возможность движения в направлении оси Z в обе стороны, но в то же время, шар сохраняет возможность перемещений вдоль осей X и Y и вращение вокруг всех трёх осей 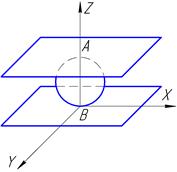X,Y,Z.

Рис. 4.2 Пример двухсторонней координатной связи абсолютно гладкого шара, расположенного между двумя плоскостями.

4.3.1.2. Базирование и базы.

Базирование – придание заготовке или изделию требуемого положения относительно выбранной системы координат.

Теоретически базирование детали (изделия и т.п.) связано с лишением ее шести степеней свободы. Придание детали требуемого положения в избранной системе координат осуществляется путем соприкосновения ее поверхностей с поверхностями детали или деталей, на которые ее устанавливают или с которыми ее соединяют. Фиксация достигнутого положения и постоянство контакта обеспечивается силами, в числе которых первым проявляется действие массы самой детали и сил трения. Реальные детали машин ограничены поверхностями, имеющими отклонения формы от своего идеального прототипа. Поэтому базируемая деталь может контактировать с деталями, определяющими ее положение лишь на отдельных элементарных площадках, условно считаемых точками контакта (рис.4.3.). В общем случае при сопряжении детали по трем поверхностям с деталями, базирующими ее, возникает шесть точек контакта. При этом точки контакта распределяются определенным образом.

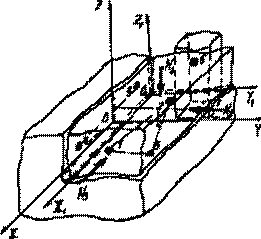
Рис.4.3. Сопряжение реальных деталей.

Базирование детали осуществляется с помощью нескольких ее базирующих поверхностей, или, короче, баз.

Базой называется поверхность, или заменяющее ее сочетание поверхностей, ось, точка, принадлежащая заготовке или изделию и используемая для базирования (рис 4.4). Как правило, к базовым поверхностям предъявляются высокие требования к их форме (отклонение от плоскостности, прямолинейности, цилиндричности, круглости, профиля продольного сечения, перпендикулярности и др.), качеству (шероховатость, волнистость, дополнительные требования к поверхностному слою: цементация, закалка и т.п.) и взаимному расположению баз (отклонение от перпендикулярности, параллельности, соосности, симметричности и др.).

На базах детали всегда можно построить жёстко связанную с ней систему координат Х₁O₁Y₁Z₁, которую принять называть собственной системой координат базируемой детали, что позволяет рассматривать базирование детали как определение положения её собственной системы координат Х₁O₁Y₁Z₁ относительно выбранной ХOYZ. Совокупность трех баз, образующих собственную систему координат заготовки (изделия, детали) называют комплектом баз.

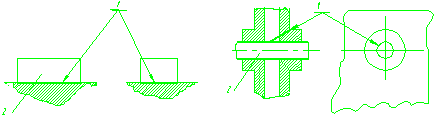
База - поверхность: 1 - база, 2 - деталь.

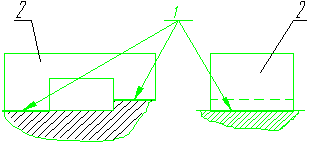
База - сочетание поверхностей: 1 – база,: 2 - деталь.

База – ось: 1 - база, 2- заготовка, 3 - губки самоцентрирующих тисков.

База – точка: 1 – база, 2 - заготовка, 3 - подпружиненный центрирующий конус приспособления.

Рис. 4.4 Виды баз.

В реальных конструкторских и технологических задачах собственная система координат Х₁O₁Y₁Z₁ может быть материализована реальными поверхностями, либо представляться мысленно, в виде плоскости, оси, точки. Например, при построении собственной системы координат вала Х₁O₁Y₁Z₁, ось Y₁ совмещена с осью его симметрии, а плоскость Х₁O₁Z₁ совмещена с торцем. Плоскости Z₁O₁Y₁ Х₁O₁Y₁ представлены мысленно, а плоскость Х₁O₁Z₁ – реальная поверхность детали (рис. 4.3).

На схемах двусторонние связи заменяются опорными точками. Опорная точка – символ одной из связей заготовки или изделия с выбранной системой координат, который изображается в виде «галочки» или «ромбика» (рис.4.5).

Рис.4.5. Изображение опорной точки: а)- вид сбоку; б) – вид сверху.

Опорные точки располагаются только на основных базах. Все опорные точки нумеруют порядковыми номерами, начиная с базы, на которой располагают наибольшее число опорных точек. При наложении какой-либо проекции одной опорной точки на другую, изображают одну точку и около неё проставляют номера совмещённых точек. Схему расположения опорных точек на детали или заготовке принято называть схемой базирования. Различают полную и неполную схемы базирования. В первом случае заготовка (деталь) лишается всех шести степеней свободы, во втором – части из них: пяти и менее.

Дата добавления: 2014-12-07