
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Цилиндрическая стенка с круглым ребром постоянной толщины
|
|
|
|
Расчет теплопередачи через трубу, оребренную снаружи кольцевыми ребрами (рис. 2.3), можно проводить по формулам (2.7) и (2.8) принимая h=R–r и умножая коэффициент эффективности Е на поправочный коэффициент 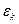 , который определяется по графику рис.(2,1)
, который определяется по графику рис.(2,1)
Коэффициент эффективности круглого ребра
 (2.1)
(2.1)
где 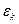 – коэффициент, определяемый по графику рис. 2.4 в зависимости от
– коэффициент, определяемый по графику рис. 2.4 в зависимости от 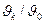 и R/r;
и R/r;  - эффективная высота ребра,
- эффективная высота ребра,  –отношение избыточных температур на конце у основания ребра.
–отношение избыточных температур на конце у основания ребра.
Параметр m определяется из выражения


Рис. 2.3. Круглое ребро постоянной толщины

Рис. 2.4. Зависимость εк=f(ϑк/ϑ0; R/r) для круглого ребра
Глава третья
ТЕПЛООБМЕН С УЧЕТОМ ВНУТРЕННИХ ИСТОЧНИКОВ
ТЕПЛОТЫ
B определенных условиях в телах могут происходить процессы выделением (поглощением) теплоты, например джоулево нагревание электропроводника, химические экзо- и эндотермические реакции, ядерные процессы в тепловыделяющих элементах (твэлах) реактора и т. п. |и процессы характеризуются мощностью внутренних источников теплоты или интенсивностью объемного тепловыделения 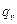 , Вт/м3.
, Вт/м3.
3.1. Однородная неограниченная пластина
Для плоской пластины ( =const), равномерно охлаждаемой обеих сторон (рис. 3.1), задана температура поверхности
=const), равномерно охлаждаемой обеих сторон (рис. 3.1), задана температура поверхности 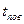 .
.

Рис. 3.1. Температурный график в пластине с учетом внутренних источников теплоты
Одномерное температурное поле пластине толщиной 2 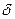
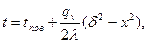 (3.1)
(3.1)
где 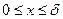
В формуле (3.1) при х=0 температура в середине толщины пластины
 (3.2)
(3.2)
Учитывая зависимость 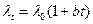 в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по форм уле
в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по форм уле
 (3.3)
(3.3)
Для плоской пластины ( =const), равномерно охлаждаемой с обеих сторон, заданы температура среды
=const), равномерно охлаждаемой с обеих сторон, заданы температура среды 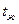 и коэффициент теплоотдачи а.
и коэффициент теплоотдачи а.
Одномерное температурное поле в пластине
 (3.4)
(3.4)
где 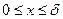
В формуле (3.4):
при х= 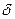 температура на поверхности пластины
температура на поверхности пластины
 (3.5)
(3.5)
при х=0 температура в середине толщины пластины
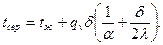 (3.6)
(3.6)
Мощность внутренних источников теплоты для пластины опреде| ляется по формулам
 (3.7)
(3.7)
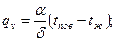 (3.8)
(3.8)
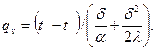 (3.9)
(3.9)
Связь между объемной 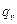 и поверхностной
и поверхностной 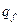 плотностями тепло выделения используется при определении теплового потока на боко вых поверхностях пластины
плотностями тепло выделения используется при определении теплового потока на боко вых поверхностях пластины

 (3.10)
(3.10)
3.2. Цилиндрический стержень
Длябесконечного стержня( =const)задана температура на оси
=const)задана температура на оси 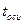 .
.
Температурное поле в стержне диаметром 
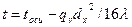 (3.11)
(3.11)
В формуле (3.8) при 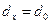 температура на поверхности стержня
температура на поверхности стержня
 (3.12)
(3.12)
С учетом зависимости 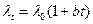 температурное поле в стержне
температурное поле в стержне
 (3.13)
(3.13)
Для стержня ( =const), равномерно охлаждаемого средой, заданы ее температура
=const), равномерно охлаждаемого средой, заданы ее температура 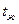 и коэффициент теплоотдачи а.
и коэффициент теплоотдачи а.
Температурное поле в стержне
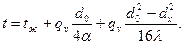 (3.14)
(3.14)
В формуле (3.14):
при  температура на оси стержня
температура на оси стержня
 (3.15)
(3.15)
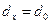 температура на поверхности стержня
температура на поверхности стержня
 (3.16)
(3.16)
Мощность внутренних источников теплоты для стержня
 (3.17)
(3.17)
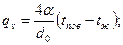 (3.18)
(3.18)
 (3.19)
(3.19)
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 603; Нарушение авторских прав?; Мы поможем в написании вашей работы!