
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
З. Цилиндрическая труба
|
|
|
|
Теплота отводится через внешнюю поверхность трубы. Температурное поле в стенке трубы с внутренним радиусом 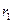 и внешним
и внешним 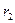
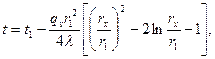 (3.20)
(3.20)
где  ,
, 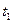 – температура на внутренней теплоизолированной поверхности трубы.
– температура на внутренней теплоизолированной поверхности трубы.
Подставляя в формулу (3.20) 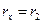 , можно получить расчетное выражение для перепада температуры в стенке
, можно получить расчетное выражение для перепада температуры в стенке
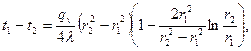 (3.21)
(3.21)
формулу для линейной плотности теплового потока
 (3.22)
(3.22)
где 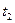 – температура на внешней поверхности трубы.
– температура на внешней поверхности трубы.
Теплота отводится через внутреннюю поверхность трубы.
Температурное поле в стенке трубы
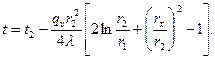 (3.24)
(3.24)
Перепад температур в стенке
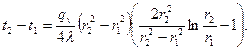 (3.25)
(3.25)
Линейная плотность теплового потока
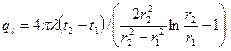 (3.26)
(3.26)
Теплота отводится через обе поверхности трубы.
Перепад температур в стенке
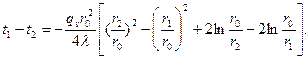 (3.27)
(3.27)
где 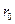 – радиус поверхности, которая имеет наибольшую температуру
– радиус поверхности, которая имеет наибольшую температуру
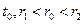 .
.
Этот радиус определяется из зависимости
 (3.28)
(3.28)
Наибольшую температуру в стенке трубы можно найти по выражению

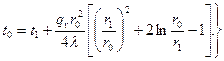 (3.29)
(3.29)
3.4. Теплообмен в условиях электрического нагрева
При прохождении электрического тока по проводнику цилиндрической формы диаметром do и длиной l температуры рассчитываются формулам (3.12) и (3.15), в которых 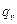 выражается через электрические параметры: I–силу тока, A; U– напряжение, В;
выражается через электрические параметры: I–силу тока, A; U– напряжение, В; 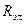 –элек трическое сопротивление проводника, Ом:
–элек трическое сопротивление проводника, Ом:
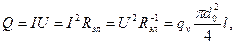 (3.30)
(3.30)
где 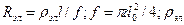 –удельное электрическое сопротивление материала проводника,Ом-м.
–удельное электрическое сопротивление материала проводника,Ом-м.
Глава четвертая
ТЕПЛОПРОВОДНОСТЬ ПРИ НЕСТАЦИОНАРНОМ РЕЖИМЕ
Нестационарная теплопроводность характеризуется изменениемтемпературного поля тела во времени и связана с изменением энтальпии тела при его нагреве или охлаждении. Безразмерная температура тела 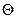 определяется с помощью числа Био Bi=al/
определяется с помощью числа Био Bi=al/  , числа Фурье Fо =а
, числа Фурье Fо =а 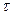 /
/  и безразмерной координаты, обозначаемой для пластины X=х/
и безразмерной координаты, обозначаемой для пластины X=х/ 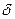 , а для цилиндра R=
, а для цилиндра R= 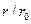 . Охлаждение (нагревание) тел происходит в среде с постоянной температурой
. Охлаждение (нагревание) тел происходит в среде с постоянной температурой 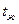 , при постоянном коэффициенте теплоотдачи а;
, при постоянном коэффициенте теплоотдачи а;  , и а – теплопроводность и температуропроводность материала тела, l – характерный размер тела (
, и а – теплопроводность и температуропроводность материала тела, l – характерный размер тела (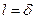 для пластины,
для пластины, 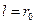 для цилиндра), х и r – текущие координаты соответственно для пластины и цилиндра.
для цилиндра), х и r – текущие координаты соответственно для пластины и цилиндра.
4.1. Тела с одномерным температурным полем
Пластина толщиной 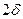 . Безразмерная температура пластины
. Безразмерная температура пластины
 (4.1)
(4.1)
где t-температура в пластине для момента времени 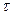 в точке с координатой х;
в точке с координатой х; 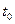 – температура пластины в начальный момент времени..
– температура пластины в начальный момент времени..
Если Fo>0,3, то температура на поверхности пластины (Х=1)
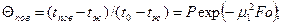 (4.2)
(4.2)
Температура на середине толщины пластины (Х=0)
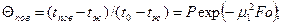 (4.3)
(4.3)
Температура внутри пластины на расстоянии х от ее средней плоскости
 (4.4)
(4.4)
где 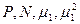 определяются по табл. 5 приложения для пластины в зависимости от числа Bi.
определяются по табл. 5 приложения для пластины в зависимости от числа Bi.
Температура  и
и 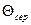 можно определить по графикам рис. П.1, П.2 по известным числам Bi и Fo.
можно определить по графикам рис. П.1, П.2 по известным числам Bi и Fo.
Цилиндр радиусом 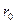 . Безразмерная температура цилиндра
. Безразмерная температура цилиндра
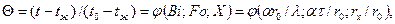 (4.15)
(4.15)
где t–искомая температура в цилиндре для радиуса  и времени
и времени 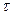 ,
,
Если Fo>0,3, то температура на поверхности цилиндра (R=1)
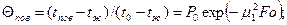 (4.6)
(4.6)
Температура на оси цилиндра (R=0)
 (4.7)
(4.7)
Температура внутри цилиндра для радиуса 
 (4.8)
(4.8)
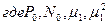 определяются по табл. 6 приложения для цилиндра в зависимости от числа Bi;
определяются по табл. 6 приложения для цилиндра в зависимости от числа Bi; 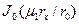 – функция Бесселя первого рода нулевого порядка (табл. 19 приложения).
– функция Бесселя первого рода нулевого порядка (табл. 19 приложения).
Температуры  и
и 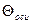 можно определить по графикам рис. П.З рП.4 Приложения по известным числам Bi и Fo.
можно определить по графикам рис. П.З рП.4 Приложения по известным числам Bi и Fo.
4.2. Тела конечных размеров
Температура определяется на основе теоремы о перемножении решений: безразмерная температура тела конечных размеров при нагревании (охлаждении) равна произведению безразмерных температур тел с бесконечным размером, при пересечении которых образовано данное конечное тело.
Цилиндр длиной 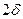 и радиусом
и радиусом 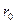 (рис. 4.1). Он образован пересечением бесконечной пластины толщиной
(рис. 4.1). Он образован пересечением бесконечной пластины толщиной 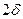 и бесконечного цилиндра радиусом
и бесконечного цилиндра радиусом 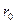 .
.
Безразмерная температуры стержня  равна
равна
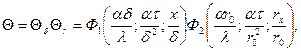 (4.9)
(4.9)
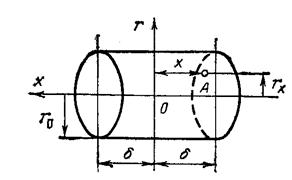
Рис. 4.1. Цилиндрический стержень длиной l =2 δ и радиусом r 0
где 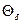 (или функция
(или функция 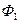 ) при Fo>0,3 определяется по формулам (4.1)–(4.3) и графикам рис. П.1 и П.2 приложения для бесконечна пластины толщиной
) при Fo>0,3 определяется по формулам (4.1)–(4.3) и графикам рис. П.1 и П.2 приложения для бесконечна пластины толщиной 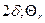 (или функция 02) при Fo>0,3 определяется по формулам (4.5)–(4.7) и графикам рис. П.З и П.4 приложения для бесконечного цилиндрического стержня радиусом
(или функция 02) при Fo>0,3 определяется по формулам (4.5)–(4.7) и графикам рис. П.З и П.4 приложения для бесконечного цилиндрического стержня радиусом 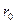 .
.
При Fo>0,3 безразмерная температура внутри цилиндрического стержня в точке с координатами х и  будет определяться аналоги но, но
будет определяться аналоги но, но 
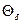 рассчитывается по формуле (4.4), a
рассчитывается по формуле (4.4), a 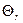 – по формуле (4.4) с использованием табл. 5 и 6 приложения.
– по формуле (4.4) с использованием табл. 5 и 6 приложения.
Параллелепипед со сторонами  (рис. 4.2). Безразмерная температура
(рис. 4.2). Безразмерная температура  или
или
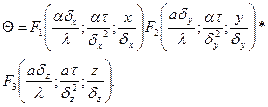 (4.10)
(4.10)
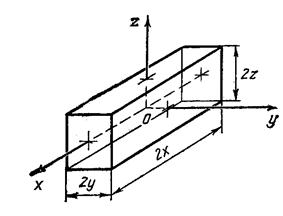
Рис. 4.2. Параллелепипед со сторонами 2х, 2у, 2z
Функции 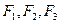 определяются по формулам (4.1)–(4.4), по табл. 5и по графикам рис. П.1 и П.2 приложения для бесконечной пластины с учетом места расположения интересующей нас точки в параллелепипеде.
определяются по формулам (4.1)–(4.4), по табл. 5и по графикам рис. П.1 и П.2 приложения для бесконечной пластины с учетом места расположения интересующей нас точки в параллелепипеде.
1.3. Расчет отданной (воспринятой) телом теплоты
Количество теплоты 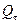 , Дж, отданной (воспринятой) телом за время t
, Дж, отданной (воспринятой) телом за время t
в процессе охлаждения (нагревания), равно
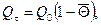 (4.11)
(4.11)
где Qo–количество теплоты, переданной за время полного охлаждения (нагревания), Дж; 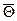 –средняя по объему безразмерная температура тела в момент времени t.
–средняя по объему безразмерная температура тела в момент времени t.
Для пластины толщиной 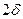 и площадью поверхности F теплота. Преданная за время полного охлаждения, равна
и площадью поверхности F теплота. Преданная за время полного охлаждения, равна
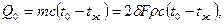 (4.12)
(4.12)
где m–масса пластины, кг; с– теплоемкость материала пластины, Дж/(кг·К); 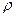 –его плотность, кг/м3.
–его плотность, кг/м3.
Средняя по объему безразмерная температура пластины в момент времени 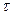 при Fo>0,3 равна
при Fo>0,3 равна
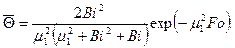 (4.13)
(4.13)
Для цилиндра радиусом 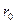 и длиной l теплота, отданная за время полного охлаждения, равна
и длиной l теплота, отданная за время полного охлаждения, равна
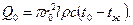 (4.14)
(4.14)
Средняя по объему безразмерная температура цилиндра в момент времени 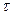 при Fo>0,3 равна
при Fo>0,3 равна
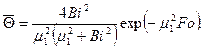 (4.15)
(4.15)
Средняя безразмерная температура цилиндра конечной длины
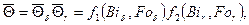 (4.16)
(4.16)
где функция 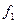 определяется по формуле (4.13), а
определяется по формуле (4.13), а 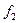 – по (4.15).
– по (4.15).
Для параллелепипеда со сторонами  (рис. 4.2) теплота, отданная за время полного охлаждения, равна
(рис. 4.2) теплота, отданная за время полного охлаждения, равна
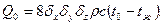 (4.17)
(4.17)
Средняя безразмерная температура параллелепипеда
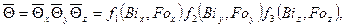 (4.18)
(4.18)
где функции 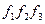 определяются по формуле (4.13).
определяются по формуле (4.13).
Если Fo<0,3, то для вычисления Q используется ряд, члены которого определяются формулами типа (4.13), (4.15), причем величины  определяются по таблицам, приведенным, например, [12].
определяются по таблицам, приведенным, например, [12].
4.4. Регулярный режим охлаждения (нагревания) тел
Теорию регулярного режима разработал Г. М. Кондратьев. Процесс охлаждения тела в среде с постоянной температурой 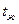 и постоянным коэффициентом теплоотдачи а можно разделить на три режима
и постоянным коэффициентом теплоотдачи а можно разделить на три режима
1) неупорядоченный– на процесс влияет начальное распределение температуры в теле;
2) регулярный– в любой точке тела относительная скорость изменения температуры, называемая темпом охлаждения (нагревания) остается постоянной и не зависит от времени;
3) стационарный – температура во всех точках тела равна температуре среды (тепловое равновесие).
В регулярном режиме темп охлаждения (нагревания), т, с-1, определенный по двум моментам времени 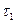 и
и  , равен
, равен
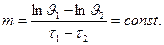 (4.19)
(4.19)
где 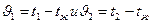 – избыточные температуры в любой точке тела в моменты времени
– избыточные температуры в любой точке тела в моменты времени 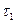 и
и  .
.
Темп охлаждения m зависит от физических свойств тела, его размеров и формы, коэффициента теплоотдачи и не зависит от времени координат.
Первая теорема Г. М. Кондратьева для регулярного режима. выражается формулой
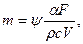 (4.20)
(4.20)
где F и V – площадь поверхности и объем тела; 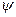 – коэффициент 1 равномерности распределения температуры в теле, определяемый следующим образом:
– коэффициент 1 равномерности распределения температуры в теле, определяемый следующим образом:
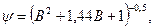 (4.21)
(4.21)
где 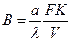 модифицированная форма числа Bi; К– коэффициент формы тела, м2.
модифицированная форма числа Bi; К– коэффициент формы тела, м2.
Коэффициент 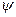 зависит от условий процесса на поверхности тел при Bi<0,l
зависит от условий процесса на поверхности тел при Bi<0,l 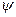 =1 (температуры, усредненные по поверхности и объем тела, одинаковы), при Bi>100
=1 (температуры, усредненные по поверхности и объем тела, одинаковы), при Bi>100 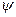 =0 (температура поверхности тела равна температуре среды).
=0 (температура поверхности тела равна температуре среды).
Вторая теорема Г. М. Кондратьева: при высокой интенсивности теплоотдачи темп охлаждения пропорционален коэффициенту температуропроводности материала тела а, 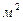 /с:
/с:
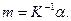 (4.22)
(4.22)
Коэффициент формы К различных тел:
для шара радиусом 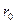
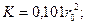 (4.23)
(4.23)
для цилиндра длиной l и радиусом 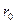
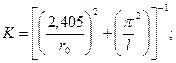 (4.24)
(4.24)
для параллелепипеда со сторонами a,b,c
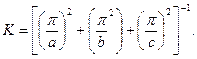 (4.25)
(4.25)
Глава пятая
ТЕОРИЯ ПОДОБИЯ ПРИМЕНИТЕЛЬНО К ТЕПЛОВЫМ ПРОЦЕССАМ
При экспериментальном изучении тепловых процессов принято выражать математическое описание процесса и расчетные уравнения в виде зависимостей между числами (критериями) подобия, представляющими собой безразмерные комплексы.
Уравнения подобия, выражая обобщенную зависимость между величинми, характеризующими процесс, справедливы для всех подобных между собой процессов. Первая теорема подобия: для подобных между собой процессов все одноименные числа подобия численно одинаковы, например Re==idem, Pr=idem. Согласно второй теореме подобия связь между числами подобия выражается в форме однозначной функциональной зависимости, например Nu=f(Re, Pr, Gr,...).
Третья теорема подобия утверждает, что условия подобия физических явлений, заключаются в подобии условий однозначности и равенстве одноименных чисел подобия, составленных из величин, входящих в| эти условия.
5.1. Числа теплового и гидромеханического подобия процессов
Нуссельта число–безразмерный коэффициент теплоотдачи
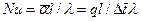 , (5.1)
, (5.1)
 -теплопроводность жидкости; l–характерный линейный размер.
-теплопроводность жидкости; l–характерный линейный размер.
Средний коэффициент теплоотдачи в формуле (5.1)
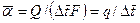
к начальному температурному напору
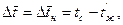 (5.2)
(5.2)
к среднеарифметическому напору
 (5.3)
(5.3)
или к среднелогарифмическому напору
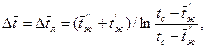 (5.4)
(5.4)
где 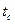 – средняя температура стенки;
– средняя температура стенки; 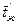 – температура набегающего потока или среднемассовая температура жидкости на входе в трубу, в теплообменник;
– температура набегающего потока или среднемассовая температура жидкости на входе в трубу, в теплообменник; 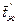 – среднемассовая температура жидкости на выходе из трубы, теплообменника.
– среднемассовая температура жидкости на выходе из трубы, теплообменника.
Если 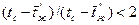 , то вместо (5.4) можно использовать (5.3), т. е.
, то вместо (5.4) можно использовать (5.3), т. е.
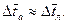 (5.5)
(5.5)
Прандтля число – безразмерная характеристика теплофизических свойств жидкости
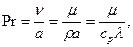 (5.6)
(5.6)
где 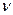 и
и  –кинематическая,
–кинематическая, 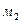 , и динамическая, Па-с, вязкости, =vp;
, и динамическая, Па-с, вязкости, =vp; 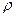 и
и 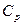 – плотность, кг/м3, и изобарная массовая теплоемкость Дж/(кг-К), жидкости; а=
– плотность, кг/м3, и изобарная массовая теплоемкость Дж/(кг-К), жидкости; а= 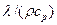 –температуропроводность жидкости,
–температуропроводность жидкости,  .
.
Пекле число – критерий теплового подобия
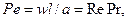 (5.7)
(5.7)
где Re – число Рейнольдса; w – характерная скорость потока, м/с
Стантона число – критерий вынужденного конвективного переноса теплоты
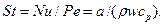 (5.8)
(5.8)
Фурье число – критерий тепловой гомохронности
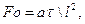 (5.9)
(5.9)
где 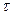 – время протекания нестационарного процесса теплопроводности
– время протекания нестационарного процесса теплопроводности
Био число–критерий краевого подобия
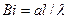 (5.10)
(5.10)
где l –характерный линейный размер твердого тела;  –теплопроводность твердого тела.
–теплопроводность твердого тела.
Тепловой критерий фазового превращения
 (5.11)
(5.11)
где r – теплота испарения (конденсации), Дж/кг; 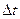 –разность температур насыщения и перегрева (переохлаждения) фазы;
–разность температур насыщения и перегрева (переохлаждения) фазы; 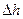 –разность энтальпий фазы в состояниях насыщения и перегрева (переохлаждения).
–разность энтальпий фазы в состояниях насыщения и перегрева (переохлаждения).
Галилея число–критерий подобия полей свободного течения
 (5.12)
(5.12)
g-ускорение свободного падения, м/с2.
Грасгофа число–-критерий свободной тепловой конвекции
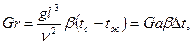 (5.13)
(5.13)
где 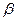 -коэффициент объемного расширения,
-коэффициент объемного расширения, 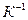 ; для идеальных газов
; для идеальных газов 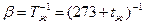 ; для капельных жидкостей приближенно
; для капельных жидкостей приближенно 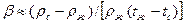 , где
, где  и
и  –плотности жидкости при
–плотности жидкости при 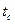 и
и 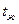 . Для воды
. Для воды 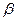 -можно определить по табл. 3 приложения.
-можно определить по табл. 3 приложения.
Релея число– критерий теплообмена при свободной конвекции
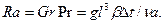 (5.14)
(5.14)
Фруда число – критерий гравитационного подобия, характеризует меру отношения сил инерции и тяжести в потоке:
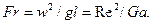 (5.15)
(5.15)
Рейнольдса число – критерий режима движения жидкости
 (5.16)
(5.16)
Эйлера число- критерий подобия полей давления
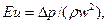 (5.17)
(5.17)
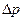 -перепад давления на участке движения жидкости.
-перепад давления на участке движения жидкости.
Архимеда число – критерий свободной конвекции
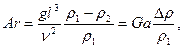 (5.18)
(5.18)
где 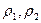 –плотности жидкости в двух точках потока.
–плотности жидкости в двух точках потока.
Определяющая температура, до которой выбираются теплофизические свойства жидкости или газа, входящие в числа подобия, указывается нижним индексом возле числа подобия: «ж», «с», «п.с»–соответственно средняя температура жидкости, стенки, пограничного слоя. Например,
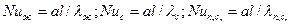 (5.19)
(5.19)
Определяющий геометрический размер также может быть указан нижним индексом возле числа подобия: l и h–длина и высота поверхности, d– диаметр трубы и т. п. Например,
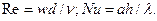 (5.20)
(5.20)
Глава шестая
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1075; Нарушение авторских прав?; Мы поможем в написании вашей работы!