Анализ зависимостей среднего квадрата смещений ионов кислорода от времени

Экспериментальные результаты и их обсуждение

Разработанный программно-аппаратный комплекс, реализующий технологию поточно-параллельных вычислений, позволил ускорить время расчетов на порядок по сравнению со специально оптимизированными версиями программ молекулярной динамики, использующими SIMD-технологии (SSE, 3Dnow!), и на два порядка по сравнению с простейшими реализациями из других работ [34] (табл. 7.2).

На его базе проводилось моделирование кристаллов UO₂ с различным числом частиц (от 2592 до 20736). Рассчитаны коэффициенты диффузии собственных ионов (в том числе, для малоподвижного урана, процессы переноса которого методом молекулярной динамики практически не исследованы) в широком диапазоне температур, включающем все три состояния: кристалл, суперионное состояние и расплав. В результате моделирования удалось воспроизвести соответствующие фазовые переходы (суперионный и плавление) и рассчитать энергии активации диффузии для разных фазовых состояний.

С использованием новой методики стало доступно моделирование систем порядка 10⁴ частиц на временах наблюдения порядка 10⁶~10⁸ шагов, что позволило обнаружить скачок коэффициента диффузии кислорода при суперионном переходе (рис. 7.5), полученные результаты находятся в согласии с имеющимися экспериментальными данными [35] и другими работами по молекулярно-динамическому моделированию [36] в пределах погрешностей эксперимента: энергия активации диффузии в кристаллической фазе составила 2.7735±0.2 эВ, а после суперионного перехода понизилась до 1.6823±0.2 эВ.

Таблица 7.2.

Сравнение скорости расчетов на кристалле из 6144 ионов

Программно-аппаратная реализация молекулярной динамики	Время, затрачиваемое на расчет
1 шаг (сек)	100.000 шагов (часы)	1.000.000 шагов (сутки)
* Простейшая реализация из работы [34] (Delphi)		416,7	173,6
* SIMD реализации авторов (С++, SSE, 3Dnow) и (С#,.NET)	1 и 1,2	27,8 и 33,3	11,6 и 13,9
MPI распараллеленная реализация авторов (кластер)	0,192	5,3	2,2
* поточно-параллельная реализация авторов (С#, asm)	0,115	3,2	1,3

* все расчеты проводились на аппаратной базе рабочей станции – AMD Ath­lon1700+, 512 DDR PC3200, Nvidia nForce2 Ultra, Nvidia GeForce6600GT; кроме MPI версии, которая запускалась на кластере из 16 процессоров AMD Opteron.

Значения коэффициентов диффузии ионов урана и кислорода в модель­ных кристаллах при заданной температуре T, в соответствии с формулой, опре­деляли по наклону зави­симостей среднего квадрата смещений ионов от време­ни:

.

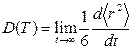Проведенные расчеты показали, что при временах моделирования, по­рядка и бόльших 100 тыс. шагов ´ 5∙10^-15 c (возрастающих с пониже­нием температуры), зависимости < r ²> от времени как для ионов кислорода, так и для ионов урана действительно в среднем вы­ходят на прямые d < r ²>/ dt = Const, что под­тверждает корректность определения коэффи­циентов диф­фузии.

Рис. 7.5. Характерная зависимость среднего квадрата смещений ионов кис­лорода от вре­мени моделирования.

По вертикальной оси отложен средний квадрат смещений < r ²>, умноженный на количество внутренних ионов O^2-, по которым проводилось усреднение, так что высоты ступенек численно равны суммам квадратов перемещений ионов в новые равновесные позиции. A – зави­симость < r ²> от времени, полученная в численном экспери­менте; B – прямая, наклон которой дает коэффициент самодиффузии кислорода при больших вре­менах моделирования; 1 - 13 – ступеньки, соответствующие конкретным перемеще­ниям ионов.

С другой стороны, оказалось, что при температурах, достаточно низ­ких по сравнению с температу­рой плавления, начальные участки зависи­мостей < r ²> от времени для ионов кислорода имеют ступенчатый характер, отсле­живающий образование и перемещение еди­ничных дефектов анион­ной подрешетки. Анализ ступенек позволил нам подтвердить диффу­зион­ный характер перемещения ионов, а также сделать некоторые выводы о механиз­мах собственного разупорядочения модельных кристаллов диоксида урана.

Характерная для сравнительно низких температур зависимость сред­него квадрата сме­щения внутренних ионов кислорода в модельных крис­таллитах от времени показана на рис. 7.5. Как отмечено выше, при обработке ступенек на этой и других аналогичных зависимостях мы считали, что каж­дая ступенька обусловлена перемещением одного или нескольких ионов кислорода из некоторых равновесных позиций в новые равновесные пози­ции, такие, из которых ионы не совершают дальнейших прыжков в те­чение временных интервалов, больших по срав­нению с длиной ступеньки. Назы­вать эти позиции равновес­ными возможно потому, что длины сту­пенек на порядки превышают времена гармонических колебаний ионов (около 10^-13с., т.е., 20-ти шагов).

Для количественного анализа ступенек, мы сравнивали их высоты (нор­мированные, как показано на рис. 7.5) с квадратами переходов между равно­весными позициями в анионной подрешетке диоксида урана, которая имеет простую кубическую структуру. Самые короткие из таких переходов пока­заны на рис. 7.6, их длины в единицах периода решетки приведены в табл. 7.3.

Как видно из рис. 7.6 и табл. 7.3, структура анионной подрешетки диоксида урана такова, что минимальные расстоя­ния между соседними равновесными позициями ионов кис­лорода равны половине периода ре­шетки (0.5 a), а квадраты этих – расстояний r ²=0.25 a ². Расчеты показали, что мини­мальные достоверно разрешимые ступеньки действительно име­ют высоты (0.25¸0.35) a ² (например, ступенька № 8 на рис. 7.5), которые могут соответ­ствовать переходам анионов кислорода в соседний вакант­ный узел (переход 1 на рис. 7.6).

Следующие по размерам ступеньки (№ 1,3 на рис. 7.5) имеют высоты около 0.5 a ² и могут соответствовать переходам ионов в вакантные позиции по диагоналям граней кислородной подрешетки (переход 2 на рис. 7.6), либо обменам позициями вдоль ребра между соседними ионами (парный пере­ход 1 на рис. 7.6).

Далее, на на графике (рис. 7.5) есть ступеньки, имеющие высоты 1.05 a ², 1.09 a ² (№5,7 на рис. 7.5 и в табл. 7.5), которые могут соответствовать обме­ну позициями между соседними ионами по диагонали грани, либо четырем последовательным скачкам анионной вакансии вдоль ребер (что равно­сильно двум скачкам по диагоналям граней).

Образование устойчивых анионных вакансий было бы невозможно без перехода некоторых анионов в устойчивые междоузельные позиции (переходы 5,6). Таким переходам на рис. 7.5 могут соответствовать ступень­ки №2,11, высотой 1.22 a ² и 0.70 a ².

На графике сравнительно низкие ступеньки, рассмотренные выше, че­редуются со высокими, в несколько раз превосходящими a ². Можно пред­положить, что высокие ступеньки обусловлены быстрым перемещением высокоподвижных вакансий сразу на несколько позиций, до рекомбинации с междоузельным ионом, либо сложным коллек­тивным движением нес­кольких ионов.

Рис. 7.6. Возможные диффузионные перемещения ионов кислорода в UO₂. По­казан фрагмент анионной плоскости системы [001]. Int – междо­узельные пози­ции; эти позиции расположены в одной плоскости с катионами U⁴⁺, на 0.25∙ a «выше», чем анионная плоскость. Квадраты длин переходов в единицах периода решетки a, под указанными номерами 1-5, приведены в табл. 7.3.

Таблица 7.3

Возможные диффузионные перемещения ионов кислорода в UO₂

№	Перемещение	D(N ∙< r ^2>), a ^2
	Переход иона в соседний вакантный узел Обмен позициями между соседними ионами	0.250 0.500
	Переход иона в соседний вакантный узел Обмен позициями между соседними ионами	0.500 1.000
	Переход иона в соседний вакантный узел Обмен позициями между соседними ионами	0.750 1.500
	Переход в ближайшую междоузельную позицию^*)	0.188
	Переход в удаленную междоузельную позицию	0.688
	Переход в удаленную междоузельную позицию	1.188
^*) Переход в ближайшую междоузельную позицию неустойчив, поскольку ион может легко вернуться обратно

Таблица 7.4

Высоты ступенек, полученных численным экспериментом при T = 2000K

№	D(N ∙< r ^2>), a ^2	№	D(N ∙< r ^2>), a ^2
	0.57		1.05
	1.22		0.26
	0.57		3.80
	2.75		3.01
	1.09		0.70
	3.10		2.71

С увеличением времени моделирования склоны ступенек из верти­кальных становятся диагональными, а сами ступеньки постепенно вырав­ниваются по высоте и сливаются в наклонную прямую. Этот процесс мож­но объяснить установлением равновесной (и неизмен­ной) концентрации дефектов, обеспечивающих постоянный коэффициент диффузии. Видно, что при температурах, порядка и меньших 2500 K, равновесие наступает после нес­кольких сотен тысяч шагов, что показывает необходимость боль­ших времен моделирования.

Дата добавления: 2014-12-07