
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Гипернормальное распределение (HN-распределение)
|
|
|
|
Дифференциальное уравнение, определяющее функцию распределения 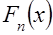 наибольшего значения случайной величины из выборки объёма
наибольшего значения случайной величины из выборки объёма  имеет следующий вид
имеет следующий вид
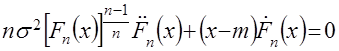 , (2)
, (2)
где 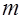 и
и 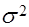 – математическое ожидание и дисперсия генеральной совокупности случайных величин.
– математическое ожидание и дисперсия генеральной совокупности случайных величин.
Нелинейное дифференциальное уравнение (2) удовлетворяет естественным краевым условиям 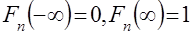 и ему соответствует функция распределения
и ему соответствует функция распределения 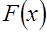 исходной случайной величины, определяемая в результате решения следующего дифференциального уравнения с теми же краевыми условиями
исходной случайной величины, определяемая в результате решения следующего дифференциального уравнения с теми же краевыми условиями
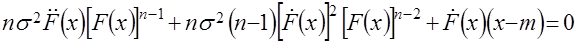 . (3)
. (3)
Дифференциальное уравнение (2), определяющее функцию распределения 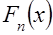 наибольшего значения, является уравнением Эйлера-Лагранжа следующей экстремальной задачи:
наибольшего значения, является уравнением Эйлера-Лагранжа следующей экстремальной задачи:
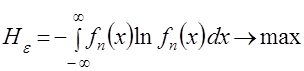 , (4)
, (4)
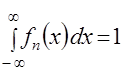 , (5)
, (5)
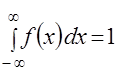 , (6)
, (6)
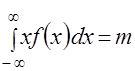 , (7)
, (7)
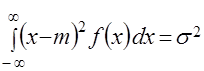 , (8)
, (8)
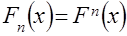 . (9)
. (9)
Для того чтобы определить функции 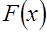 и
и 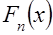 , обеспечивающие максимум функционала (4) при наличии голономной связи (9) и при изопериметрических условиях (5)-(8), необходимо использовать теоремы вариационного исчисления и определить множители Лагранжа.
, обеспечивающие максимум функционала (4) при наличии голономной связи (9) и при изопериметрических условиях (5)-(8), необходимо использовать теоремы вариационного исчисления и определить множители Лагранжа.
Согласно известным теоремам вариационного исчисления введем множители и функцию Лагранжа 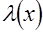 ,
, 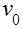 ,
, 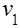 ,
, 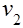 и составим уравнение Эйлера- Лагранжа для расширенной функции
и составим уравнение Эйлера- Лагранжа для расширенной функции
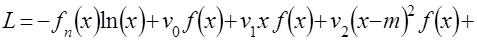 ,
,
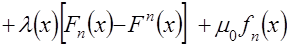 .
.
Так как 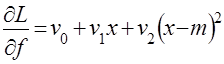 ,
,
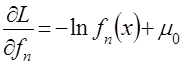 ,
, 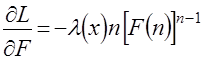 ,
, 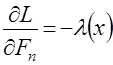 ,
,
то уравнения Эйлера-Лагранжа для расширенной функции имеют вид:
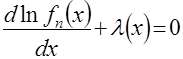 , (10)
, (10)
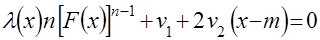 .
.
Последнее уравнение с учётом (10) можно записать виде:
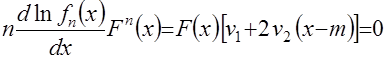 .
.
После подстановки 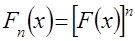 уравнение экстремалей в рассматриваемой вариационной задаче имеют вид:
уравнение экстремалей в рассматриваемой вариационной задаче имеют вид:
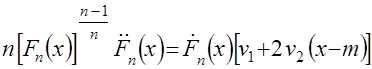 (11)
(11)
и
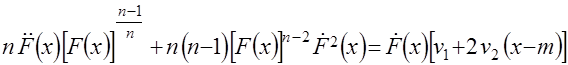 .(12)
.(12)
Проинтегрируем уравнение (12) по области задания функции распределения 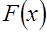 , применяя к первому слагаемому интегрирование по частям. В силу определенных свойств функции распределения и краевых условий можно убедиться, что интеграл от левой части уравнения (12) будет равен 0, а множителе Лагранжа
, применяя к первому слагаемому интегрирование по частям. В силу определенных свойств функции распределения и краевых условий можно убедиться, что интеграл от левой части уравнения (12) будет равен 0, а множителе Лагранжа 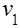 и
и 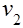 будут связаны с математическим ожиданием следующим конечным соотношением:
будут связаны с математическим ожиданием следующим конечным соотношением:
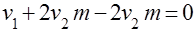 .
.
Отсюда следует 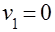 .
.
Умножив левую и правую части уравнения (12) на независимую переменную и проинтегрировав аналогичным образом полученное уравнение, можно найти второе конечное соотношение, связывающее множитель 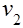 с математическим ожиданием и дисперсией. Действительно, так как
с математическим ожиданием и дисперсией. Действительно, так как
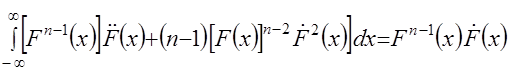 ,
,
то интегрирование левой части полученного в результате умножения на независимую переменную нового дифференциального уравнения дает следующий результат
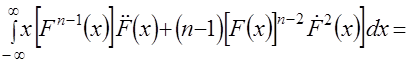
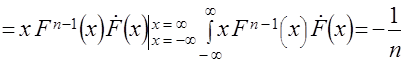 ,
,
(первое слагаемое после раскрытия неопределенности дает 0).
Таким образом 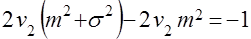
Отсюда следует, что 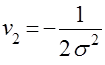 .
.
Подстановка множителей Лагранжа 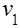 и
и 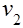 в дифференциальное уравнение (11) позволяет убедиться в справедливости дифференциальных уравнений (2) и (3).
в дифференциальное уравнение (11) позволяет убедиться в справедливости дифференциальных уравнений (2) и (3).
Эти уравнения неразрешимы в квадратах при  , что не позволяет в аналитическом виде представить функцию гипернормального распределения. В Приложении представлены значения функции гипернормального распределения и его плотности для целочисленных параметров
, что не позволяет в аналитическом виде представить функцию гипернормального распределения. В Приложении представлены значения функции гипернормального распределения и его плотности для целочисленных параметров  от 1 до 10, удовлетворяющих решению краевой задачи (2). Вычисление значений функций
от 1 до 10, удовлетворяющих решению краевой задачи (2). Вычисление значений функций 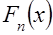 произведено для стандартных условий
произведено для стандартных условий 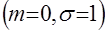 . Переход от заданных значений случайных величин к табличным производится с помощью
. Переход от заданных значений случайных величин к табличным производится с помощью
следующей зависимости
 .
.
Таблицы четырехзначные, такой выбор числа знаков обусловлен тем, что в практике исходные данные для вероятностных расчетов известны, как правило, с точностью не более чем 2-3 знака после запятой. Усечение таблицы значений функции гипернормального распределения связано с основными свойствами этого распределения, которые рассматриваются ниже.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 893; Нарушение авторских прав?; Мы поможем в написании вашей работы!