
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод построения законов распределения статистик
|
|
|
|
Введение
В данном разделе рассматриваются статистики малых выборок, разбирается метод построения законов распределения статистик, изучаются законы распределения коэффициента вариации и способы нормализации случайных величин.
После изучения данного раздела рекомендуется ответить на вопросы для самопроверки и на вопросы теста 6.
В случае если ответы на какие-либо вопросы вызовут затруднение или неуверенность, рекомендуется прочитать учебное пособие Мартыщенко, Л.А. Системное моделирование. Ч. II: учебное пособие /Л.А. Мартыщенко, Е.С. Голик, О.В. Афанасьева. – СПб.: Изд-во СЗТУ, 2008. – 102 с., (с. 63 – 88).
Идентификация случайных процессов, экспресс-оценка момента их «разладки» и прогнозирование дальнейшего их развития на основе первых наблюдений может быть сведена к процедуре проверки статистических гипотез. В соответствии с этим в тестах проверки небольших последовательностей случайных чисел (коротких динамических рядов) необходимо использование некоторых функций от наблюдаемых случайных величин по терминологии Р.Фишера (статистик), законов их распределений и критериев проверки гипотез. Многие вводимые далее в рассмотрение статистики имеют форму  , где
, где 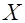 и
и 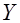 независимые случайные величины и
независимые случайные величины и  . Обозначим их функции распределения через
. Обозначим их функции распределения через  и
и  , а их плотности через
, а их плотности через 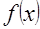 и
и  соответственно. Так как величина
соответственно. Так как величина 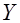 предполагается положительной, то
предполагается положительной, то  сосредоточена на интервале
сосредоточена на интервале  , и поэтому
, и поэтому
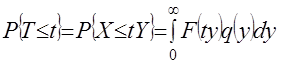 , (1)
, (1)
дифференцируя, находим, что отношение  обладает плотностью
обладает плотностью
 . (2)
. (2)
Такой прием называется рандомизацией [12] и означает рассмотрение знаменателя величины  как случайной величины
как случайной величины 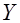 .
.
Используя метод рандомизации, докажем ряд теорем, которые окажутся полезными в дальнейших приложениях.
Теорема 1. Пусть 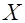 и
и 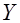 – независимые случайные величины, плотности которых имеют вид
– независимые случайные величины, плотности которых имеют вид  (3)
(3)
и 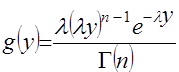 , (4) тогда отношение
, (4) тогда отношение  обладает плотностью
обладает плотностью
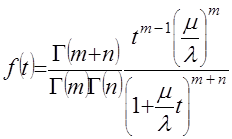 . (5)
. (5)
Доказательство. В соответствие с (2)


 . (6)
. (6)
В последнем выражении интеграл является интегралом от плотности гамма-распределения и, естественно, равен единице.
После несложных преобразований соотношение (6) может быть преобразовано в выражение для плотности (5). Теорема доказана.
Из теоремы 1. в силу большой общности гамма-распределения вытекает ряд полезных следствий, позволяющих оценить момент разладки простейшего потока, потока Эрланга и др. Так, например, если отношение 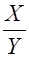 представляет собой отношение двух показательно распределенных случайных независимых величин с параметром
представляет собой отношение двух показательно распределенных случайных независимых величин с параметром 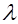 , то плотность их отношения
, то плотность их отношения 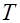 имеет вид
имеет вид  . (7)
. (7)
Если случайная величина 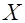 распределена по экспоненциальному закону с параметром
распределена по экспоненциальному закону с параметром 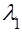 , а величина
, а величина 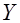 распределена по экспоненциальному закону с параметром
распределена по экспоненциальному закону с параметром 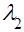 , то плотность их отношения имеет вид
, то плотность их отношения имеет вид
 , (8)
, (8)
где  .
.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 458; Нарушение авторских прав?; Мы поможем в написании вашей работы!