Асимптотические свойства гипернормального распределения

При больших (более 10) дифференциальное уравнение (2) можно заменить приближенным и найти аналитическое решение для квантильной функции.

Для стандартных условий 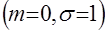дифференциальное уравнение (2) при 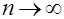может быть представлено в виде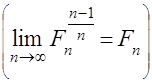

.

Нетрудно проверить, что замена независимой переменной позволяет преобразовывать это уравнение к виду

.

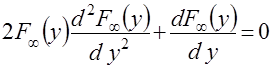Разделяя переменные и интегрируя, находим .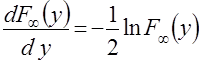

Отсюда следует ,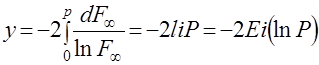

где и – и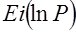нтегральный логарифм и интегральная показательная функция соответственно.

Осуществляя обратный переход от 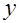до и от стандартных условий к естественным, можно получить функцию квантилей предельного гипернормального распределения

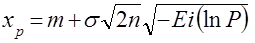, . (13)

Таким образом, функция квантилей гипернормального распределения асимптотически приближается к функции (13). Это свойство рассмотренных экстремальных распределений позволяет описать и прогнозировать с определенным уровнем доверия 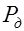экстремальные характеристики по ограниченной информации.

В общем случае можно показать, что дифференциальному уравнению (2) соответствует нелинейное дифференциальное уравнение, относительно квантильной функции

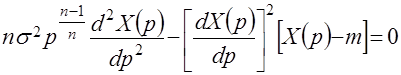(14)

с граничными условиями

, . (15)

Для стандартных условий 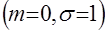это уравнение имеет вид

, (16)

решение которого, представленное в виде ряда, имеет следующий вид

. (7)

Значения коэффициентов 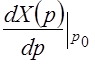, полученные в результате решения исходного уравнения, представлены в табл. 1.

Таблица 1. Значение коэффициентов

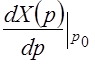
	2,648	2,727	2,940	3,158	3,389	3,784	3,967	4,139	4,141
	0,3804	0,2993	0,2612	0,2431	0,2355	0,2210	0,2162	0,2116	0,2114

Математическое ожидание и дисперсия случайной величины для предельного гипернормального распределения определяются по формулам

,

.

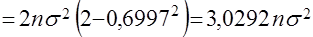Значения функции предельного гипернормального распределения , аргументом которого является величина представлены в табличной форме.

Математические ожидания и дисперсии для гипернормального распределения при малых 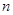представлены для стандартных условий 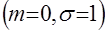в табл. 2.

Таблица 2. Математические ожидания и дисперсии

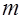
		0,4634	0,6865	0,9764	1,1355	1,2458	1,4656	1,5504	1,6748	1,6792
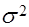
		1,1077	1,3694	1,6622	2,0190	2,3316	2,9620	3,3127	3,5722	3,6438

Остановимся еще на одном случае асимптотического поведения гипернормального распределения. Пусть 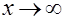(практически при ), естественным следствием из этого условия является . Тогда дифференциальное уравнение (2) может быть представлено для стандартных условий 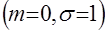в виде

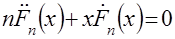. (18)

Разделяя переменные, находим , (19)

где – плотность гипернормального распределения.

Интегрирование уравнения (10) позволяет убедиться в справедливости следующего утверждения.

При больших значениях аргумента гипернормальное распределение асимптотически стремится к нормальному распределению с плотностью

. (20)

Дата добавления: 2014-12-07