Энтропийные метрики

Традиционно сложилось так, что в математической статистике широкое распространение получили критерии согласия 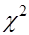, 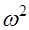и критерий Колмогорова. Безоговорочное применение этих критериев привело к формированию такого интуитивного понятия как эффект малой и большой выборки. Очевидно, что необходимость введения этого понятия обусловлена объективным существованием пределов работоспособности перечисленных выше критериев.

С этих позиций случайную выборку наблюдаемых значений случайных величин можно считать малой, если извлекаемая из нее с помощью определенного математического аппарата информация не может служить основанием для принятия достоверного решения, удовлетворяющего цели исследования, в условиях объективно существующей неопределённости.

Основной задачей математической статистики является разработка методов, позволяющих извлекать возможно более полную информацию из ограниченного объёма наблюдаемых величин. Поэтому аналитический аппарат теории информации представляется целесообразным использовать для оценки «малости» выборок. С этой целью введем в рассмотрение энтропийные метрики, характеризующие степень близости выборки генеральной совокупности. Заметим, что метрика-это расстояние между двумя точками (элементам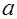и) и 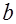множества 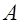, где 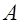– действительная числовая функция (в рассматриваемом случае энтропия 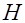), удовлетворяющая следующим условиям: 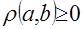, причем 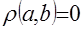тогда и только тогда, когда ; ; .

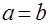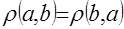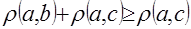Если функция распределения 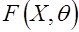описывает генеральную совокупность случайных величин 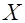и зависит от конечного числа параметров 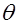, то по определению теоретическая мера относительной неопределенности распределения вероятностей определяется следующим образом

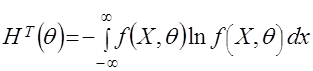. (36)

Оценка неизвестного параметра 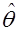по выборке 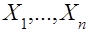является величиной случайной и по вероятности в силу свойства состоятельности оценки сходится к истинному значению 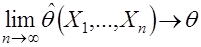. (37)

Очевидно, что разность энтропий 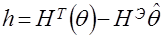. (38)

будет характеризовать степень близости эмпирического аналога генеральной совокупности (выборки) ее истинному значению.

Энтропийная метрика (38) в силу зависимости от параметра 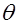является величиной случайной и зависит от объёма выборки . В качестве примеров рассмотрим зависимость плотности распределения метрики (38) 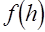для выборки из равномерного, нормального и экспоненциального распределений, наиболее распространенных в статистических исследованиях.

Для нормального закона распределения случайных величин 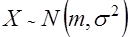энтропия определяется зависимостью

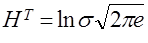. (39)

Выборочная энтропия 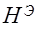соответственно определится следующим образом

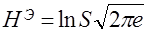. (40)

Следовательно, 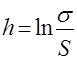. (41)

Плотность вероятности выборочного среднеквадратического отклонения 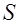имеет вид 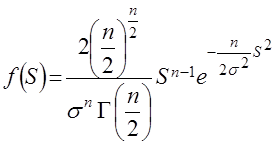. (42)

Тогда плотность распределения метрики 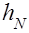определится следующим образом

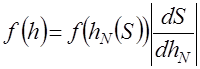. (43)

Таким образом, плотность распределения метрики 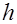будет иметь вид

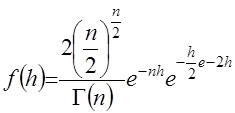. (44)

Используя подстановку 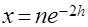, формулу (3.52) можно преобразовать в плотность 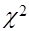-распределения 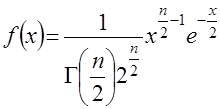. (45)

С помощью таблиц 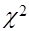-распределения, осуществляя обратное преобразование 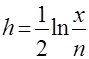, можно найти зависимость доверительной вероятности 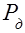(или уровня значимости 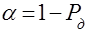) от метрики 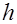и объёма выборки .

Так, например, при уровне значимост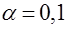и и 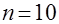мера близости эмпирического нормального распределения генеральной совокупности 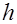составляет 0,36. Естественно, что по мере увеличения объёма выборки мера близости будет уменьшаться. Например, при 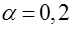и объёме выборки 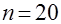метрика 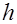составляет уже .

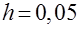Вопросы для самопроверки по разделу 6

1. В чем суть метода рандомизации случайных величин?

2. Чем обусловлено введение в рассмотрение выборочного распределения коэффициента вариации?

3. Что такое коэффициент вариации?

4. В чем заключается порядок формирования непараметрической статистики малых выборок при проверке небольших последовательностей случайных чисел на нормальность?

5. Каков порядок использования -критерия нормальности Шапиро-Уилка?

6. Для чего вводятся в рассмотрение тестовые статистики?

7. С помощью чего возможно идентифицировать короткие динамические ряды и малые выборки из гауссовских совокупностей по ограниченной информации?

8. В чем заключается основная задача математической статистики?

9. Что характеризуют энтропийные метрики?

Раздел 7. Примеры применения вероятностных методов прогнозирования сложных систем

Дата добавления: 2014-12-07