Формализация слабоструктурированных и неструктурированных задач экономики 2 страница

.

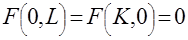С производственной функцией связаны вполне определенная экономическая интерпретация и некоторые показатели, используемые в экономическом анализе, прежде всего, это производительность труда и предельная производительность труда

.

Наиболее часто для квазистатического описания экономической динамики используются производственные функции с постоянной эластичностью замещения (CES-функции), имеющие вид

, (1)

где – константы.

Постоянству эластичности замещения (Constant Elasticity of Substitution – CES) соответствует условие

, (2)

где 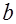– коэффициент регрессии в линейной зависимости (в логарифмическом масштабе) производительности труда и предельной производительности труда

. (3)

Производственная функция Кобба-Дугласа является предельным вариантом CES-функции (1) при , (4)

где и – коэффициенты эластичности, определяющие оптимальную пропорцию интенсивности затрат факторов и .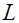

Для производственной функции Кобба-Дугласа эластичность замещения равна единице (основные фонды и трудовые ресурсы в одинаковой мере замещают друг друга).

Вторым предельным вариантом CES-функции является функция с фиксированными пропорциями в зависимости (1)

(5)

Для производственной функции с фиксированными пропорциями эластичность замещения нулевая: основные фонды и трудовые ресурсы не могут замещать друг друга, а должны использоваться в заданной пропорции, избыток фондов или трудовых ресурсов не увеличивают выпуска, что соответствует неизменности рабочих режимов технологических процессов.

Производственная функция Кобба-Дугласа и (в несколько меньшей степени) функция полезности Кобба-Дугласа стали традиционным средством анализа экономических вопросов. Однако их применение предлагает принятие довольно суровых ограничений. Например, требования гомотопической эквивалентности и единичной эластичности замены. Заметим, что общий вид гомотетичных производственных функций может быть записан как , где – функция, монотонная по , а – функция первой степени однородности по и 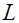. Этот класс функций дает возможность моделировать изменение отдачи от масштаба, равно как и эластичности замены с изменением уровня выпуска. Постулирование ограничений и допущений, принятых при формализации CES-функций, обусловливают необходимость проведения информационно-статистического анализа исходной _пии_миической информации. Достоверность основного постулата теории производственных функций (постоянства эластичности замещения) определяется законом распределения коэффициента регрессии.

Регрессионный анализ является одним из наиболее распространенных методов обработки результатов наблюдений при изучении зависимостей в экономике и в других областях.

Проблема регрессионного анализа в экономике характерна тем, что о распределениях изучаемых величин нет достаточной информации. Целью регрессионного _пиилиза является определение общего вида уравнения регрессии, построение статистических оценок неизвестных параметров, входящих в уравнение регрессии, и проверка статистических гипотез о коэффициентах регрессии. При изучении связи между двумя величинами по результатам наблюдений предполагается, что одна из них имеет некоторое распределение вероятностей при фиксированном значении другой. В общем случае результаты наблюдений представляют собой выборку из совокупности с некоторым двумерным распределением вероятностей. Формализацию такого распределения по ограниченной информации мы рассмотрим ниже. Использование регрессии обычно производится методами, основанными на принципах средней квадратичной регрессии. Оценка известных коэффициентов регрессии осуществляется методом наименьших квадратов. Этот метод в предположении нормальной распределенности результатов наблюдений приводит к оценкам, совпадающим с оценками наибольшего правдоподобия. Оценки, полученные этим методом, оказываются в некотором смысле наилучшими и в случае отклонения от нормальности, если только объем выборки достаточно велик. При ограниченном объеме выборки представляется целесообразным результаты наблюдений нормализировать. Соответствующие методы нормализации случайных величин будут рассмотрены ниже.

Если заданы пар наблюденных значений из двумерного распределения, то моменты и другие характеристики выборки определяются следующим образом

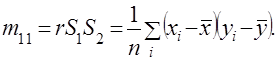(6)

Коэффициенты линейной средней квадратической регрессии для генеральной совокупности определяются в результате минимизации функции

,

где 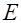– оператор определения математического ожидания. Решение этой экстремальной задачи дает единственное решение

, (7)

где 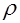– коэффициент корреляции,

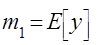, – средние значения величин 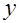и .

Прямая средней квадратической регрессии в этом случае имеет вид

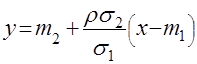. (8)

Соответствующие коэффициенты регрессии для выборки могут быть записаны следующим образом

, . (9)

Достаточно рассмотреть выборочное распределение величины (распределение для получается с помощью перестановки индексов).

Выражение для плотности вероятности выборочного коэффициента регрессии имеет вид (К.Пирсон):

, (10)

где – детерминант матрицы вторых моментов .

Если ввести новую величину

, (11)

то можно показать, что 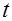распределено по закону Стьюдента с степенью свободы. Плотность вероятности (4.10) содержит все три теоретических момента и и, если необходимо оценить гипотетическое (истинное) значение коэффициента регрессии , то представляется целесообразным рассмотреть величину

, (12)

в которой характеристики совокупност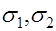и и 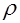заменены соответствующими выборочными характеристиками и 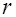, а множитель заменен на 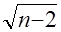. В этом случае статистика (12) имеет распределение Стьюдента с 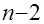степенями свободы.

Используя распределение Стьюдента, можно поставить и решить задачу проверки статистических гипотез о равенстве единице или нулю коэффициента регрессии в зависимости (3). Такое решение позволяет оценить с определенной долей вероятности предпочтительность предельных вариантов CES-функций: функции Кобба-Дугласа (4) или функции с фиксированными пропорциями (5). Решение этой проблемы идентификации представляется целесообразным рассмотреть с позиций теории распознавания образов.

Анализ задач распознавания явлений в случае, когда между признаками объектов и классами, к которым они могут быть отнесены, существуют вероятностные связи, показывает, что построение алгоритмов распознавания может быть основано на результатах теории статистических решений. Сущность такого подхода в теории распознавания образов заключается в следующем. Пусть совокупность объектов подразделена на классы 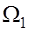и , а для характеристики объектов используется признак . Известны описания классов – условные плотности распределения вероятностей и значений признака объектов классов 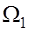и . В результате эксперимента определено значение признака распознаваемого объекта.

Чтобы определить, к какому классу отнести объект вводят некоторое значение признака 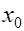и следующее правило принятия решений: если наблюдаемое значение признака у распознаваемого объекта 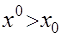, то объект следует отнести к классу 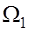, если - к классу . Если объект относится к классу 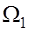, а его считают объектом класса , то совершена ошибка (ошибка 1 рода), условная вероятность которой 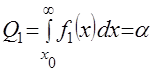. (13)

(по терминологии теории статистических решений, ошибочно выбрана гипотеза , в то время как справедлива гипотеза 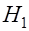). Наоборот, если справедлива гипотеза , а отдано предпочтение гипотезе 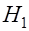, то совершена ошибка второго рода, условная вероятность которой , (14)

(по терминологии теории статистических решений, ошибочно выбрана гипотеза 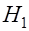, в то время как справедлива гипотеза ).

Наглядное представление о ситуации принятия решений в теории распознавания образов дает табл. 1.

Таблица 1. Варианты принятия статистического решения

Заключение по	гипотезе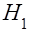
гипотезе	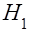Верна	Неверна (верна )
Принята	(правильное решение)	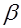(ошибка второго рода)
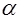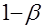Отвергнута (принята )	(ошибка первого рода)	(правильное решение)

Соображения, которыми руководствуются в теории распознавания образов при выборе значения признака 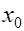(при разделении пространства признаков на два пространства), основаны на учете потерь, сопряженных с правильными и ошибочными решениями. Однако при анализе минимального объема информации (при анализе коротких динамических рядов) в интересах прогнозирования, идентификации экономических процессов и решения ряда других задач представляется целесообразным сформулировать принцип синтеза безальтернативных гипотез, сущность которого заключается в следующем.

По результатам статистического анализа может быть принято правильное решение относительно гипотезы 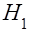с вероятностью ()

(15)

или гипотезы с вероятностью (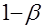) (16)

где – наблюдаемое (расчетное) значение статистики критерия.

Если нет соображений неформального порядка о необходимости разделения пространства признаков на две подобласти, а это наиболее типовая ситуация статистического анализа малых выборок, то вполне логично допустить, что результаты наблюдений (элементы) выборки можно описать композицией законов распределения и 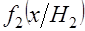с весами, равными соответственно () и ().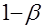

Следовательно, для гипотезы , используя условие (15) и распределение Стьюдента, получим 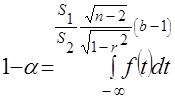, (17)

и для гипотезы , (18)

где – плотность 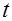-распределения Стьюдента с 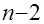степенью свободы.

С помощью статистических таблиц для 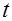-распределения можно определить интегралы (17) и (18) и после нормировки полученных значений вероятностей найти весовые коэффициенты, соответствующие производственным функциям (4) и (5). Отсюда следует, что комплексированная производственная функция с постоянной эластичностью замещения может быть представлена в виде следующей CES-функции

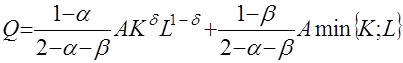. (19)

В качестве примера определим структуру функции Кобба-Дугласа на основе анализа основных технико-экономических показателей деятельности «Торговый Дом СУ-1», представленных в табл.2.

Нетрудно отметить, что производительность труда (в логарифмическом масштабе) составила, соответственно, годам 5,01; 4,80 и 6,757, а предельная производительность труда , соответственно, 5,09; 4,82 и 6,865.

Для определения коэффициента регрессии необходимо проверить статистическую гипотезу о принадлежности этих малых выборок нормальной совокупности. С этой целью используя критерий где – члены вариационного ряда, построенного по рассчитанным значениям параметров и , определим расчетные значения критериев

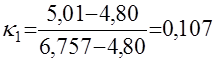
и значения функций распределения этих не параметрических статистик

и аналогично

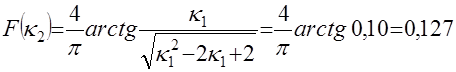
Таким образом, с вероятностью 0,9…0,87 можно утверждать, что не выявлено противоречие о принадлежности полученных выборок нормальной совокупности (заметим, что в условиях малых выборок эти вероятностные оценки являются достаточно надежными). Следовательно, для определения коэффициента регрессии в линей ной зависимости (в логарифмическом масштабе) производительности и предельной производительности возможно изменение метода наименьших квадратов:

.

Отсюда следует, что (соответственно, параметр ).

Используя функции распределения Стьюдента по приведенным выше формулам, определим ошибки первого и второго рода и .

Таблица 2. Основные технико-экономические показатели деятельности «Торговый Дом СУ-1» за 1997-1999 гг.

№ п.п.	Показатели	Ед. изм.	1997 факт	1998 факт	1999 факт
1.	Объем выполненных подрядных работ	тыс. руб.
	В т.ч. собственными силами	«
2.	Численность работающих, всего	чел.
	В том числе рабочих	«
3.	Выработка на одного работающего	тыс. руб./год	151,2	186,2	209,5
4.	Средняя заработная плата, всего	руб./мес.
	В т.ч.рабочих	«
	ИТР и служащих	«
5.	Балансовая прибыль	тыс. руб.
6.	Кредиторская задолженность	«		«625
7.	Дебиторская задолженность	«
8.	Наличие собственных оборотных средств	«
9.	Наличие строительных машин и механизмов, всего	шт.	–
	В т.ч. КамАЗ 5410	«
	КамАЗ 53202	«
	Растворный узел с ПУ	«

Следовательно, для рассмотренного примера структуру производственно функции целесообразно представить виде

Таким образом, полученные экономиико-математические модели производственного процесса позволяет поставить и решить следующую оптимизационную задачу.

Если ввести в рассмотрение удельные затраты на создание основных фондов и трудовых ресурсов ( и ), то задача минимизации затрат сводится к задаче на

условный экстремум

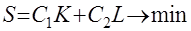(20)

при ограничении (19).

В результате решение задачи (20) и (19) можно получить оптимальное соотношение между основными фондами и трудовыми ресурсами в виде следующих отношений

(21)

или

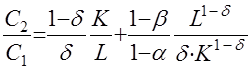(22)

в зависимости от вида функции (19).

Дата добавления: 2014-12-07