Цепные реакции. 2 страница

3 ТЕРМОДИНАМИКА РАСТВОРОВ

Существование абсолютно чистых веществ невозможно – всякое вещество обязательно содержит примеси, или, иными словами, всякая гомогенная система многокомпонентна. Если имеющиеся в веществе примеси в пределах точности описания системы не оказывают влияния на изучаемые свойства, можно считать систему однокомпонентной; в противном случае гомогенную систему считают раствором.

Раствор – гомогенная система, состоящая из двух или более компонентов, состав которой может непрерывно изменяться в некоторых пределах без скачкообразного изменения её свойств.

Раствор может иметь любое агрегатное состояние; соответственно их разделяют на твердые, жидкие и газообразные (последние обычно называют газовыми смесями). Обычно компоненты раствора разделяют на растворитель и растворенное вещество. Как правило, растворителем считают компонент, присутствующий в растворе в преобладающем количестве либо компонент, кристаллизующийся первым при охлаждении раствора; если одним из компонентов раствора является жидкое в чистом виде вещество, а остальными – твердые вещества либо газы, то растворителем считают жидкость. С термодинамической точки зрения это деление компонентов раствора не имеет смысла и носит поэтому условный характер.

Одной из важнейших характеристик раствора является его состав, описываемый с помощью понятия концентрация раствора. Ниже дается определение наиболее распространенных способов выражения концентрации и формулы для пересчета одних концентраций в другие, где индексы А и В относятся соответственно к растворителю и растворенному веществу.

Молярная концентрация С – число молей ν_В растворенного вещества в одном литре раствора.

Нормальная концентрация N – число молей эквивалентов растворенного вещества (равное числу молей ν_В, умноженному на фактор эквивалентности f) в одном литре раствора.

Моляльная концентрация m – число молей растворенного вещества в одном килограмме растворителя.

Процентная концентрация ω – число граммов растворенного вещества в 100 граммах раствора.

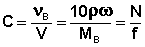(III.1)

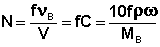(III.2)

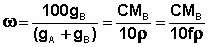(III.3)

Еще одним способом выражения концентрации является мольная доля X – отношение числа молей данного компонента к общему числу молей всех компонентов в системе.

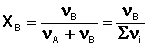(III.4)

3.1 ОБРАЗОВАНИЕ РАСТВОРОВ. РАСТВОРИМОСТЬ

Концентрация компонента в растворе может изменяться от нуля до некоторого максимального значения, называемого растворимостью компонента. Растворимость S – концентрация компонента в насыщенном растворе. Насыщенный раствор – раствор, находящийся в равновесии с растворенным веществом. Величина растворимости характеризует равновесие между двумя фазами, поэтому на неё влияют все факторы, смещающие это равновесие (в соответствии с принципом Ле Шателье – Брауна).

Образование раствора является сложным физико-химическим процессом. Процесс растворения всегда сопровождается увеличением энтропии системы; при образовании растворов часто имеет место выделение либо поглощение теплоты. Теория растворов должна объяснять все эти явления. Исторически сложились два подхода к образованию растворов – физическая теория, основы которой были заложены в XIX веке, и химическая, одним из основоположников которой был Д.И. Менделеев. Физическая теория растворов рассматривает процесс растворения как распределение частиц растворенного вещества между частицами растворителя, предполагая отсутствие какого-либо взаимодействия между ними. Единственной движущей силой такого процесса является увеличение энтропии системы ΔS; какие-либо тепловые или объемные эффекты при растворении отсутствуют (ΔН = 0, ΔV = 0; такие растворы принято называть идеальными). Химическая теория рассматривает процесс растворения как образование смеси неустойчивых химических соединений переменного состава, сопровождающееся тепловым эффектом и изменением объема системы (контракцией), что часто приводит к резкому изменению свойств растворенного вещества (так, растворение бесцветного сульфата меди СuSО₄ в воде приводит к образованию окрашенного раствора, из которого выделяется не СuSО₄, а голубой кристаллогидрат СuSО₄·5Н₂О). Современная термодинамика растворов основана на синтезе этих двух подходов.

В общем случае при растворении происходит изменение свойств и растворителя, и растворенного вещества, что обусловлено взаимодействием частиц между собой по различным типам взаимодействия: Ван-дер-Ваальсового (во всех случаях), ион-дипольного (в растворах электролитов в полярных растворителях), специфических взаимодействий (образование водородных или донорно-акцепторных связей). Учет всех этих взаимодействий представляет собой очень сложную задачу. Очевидно, что чем больше концентрация раствора, тем интенсивнее взаимодействие частиц, тем сложнее структура раствора. Поэтому количественная теория разработана только для идеальных растворов, к которым можно отнести газовые растворы и растворы неполярных жидкостей, в которых энергия взаимодействия разнородных частиц E_A-B близка к энергиям взаимодействия одинаковых частиц E_A-A и E_B-B. Идеальными можно считать также бесконечно разбавленные растворы, в которых можно пренебречь взаимодействием частиц растворителя и растворенного вещества между собой. Свойства таких растворов зависят только от концентрации растворенного вещества, но не зависят от его природы.

3.1.1 Растворимость газов в газах

Газообразное состояние вещества характеризуется слабым взаимодействием между частицами и большими расстояниями между ними. Поэтому газы смешиваются в любых соотношениях (при очень высоких давлениях, когда плотность газов приближается к плотности жидкостей, может наблюдаться ограниченная растворимость). Газовые смеси описываются законом Дальтона:

Общее давление газовой смеси равно сумме парциальных давлений всех входящих в неё газов.

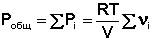(III.5)

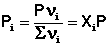(III.6)

3.1.2 Растворимость газов в жидкостях

Растворимость газов в жидкостях зависит от ряда факторов: природы газа и жидкости, давления, температуры, концентрации растворенных в жидкости веществ (особенно сильно влияет на растворимость газов концентрация электролитов).

Наибольшее влияние на растворимость газов в жидкостях оказывает природа веществ. Так, в 1 литре воды при t = 18 °С и P = 1 атм. растворяется 0.017 л. азота, 748.8 л. аммиака или 427.8 л. хлороводорода. Аномально высокая растворимость газов в жидкостях обычно обусловливается их специфическим взаимодействием с растворителем – образованием химического соединения (для аммиака) или диссоциацией в растворе на ионы (для хлороводорода). Газы, молекулы которых неполярны, растворяются, как правило, лучше в неполярных жидкостях – и наоборот. Зависимость растворимости газов от давления выражается законом Генри – Дальтона:

Растворимость газа в жидкости прямо пропорциональна его давлению над жидкостью.

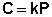(III.7)

Здесь С – концентрация раствора газа в жидкости, k – коэффициент пропорциональности, зависящий от природы газа. Закон Генри – Дальтона справедлив только для разбавленных растворов при малых давлениях, когда газы можно считать идеальными. Газы, способные к специфическому взаимодействию с растворителем, данному закону не подчиняются.

Растворимость газов в жидкостях существенно зависит от температуры; количественно данная зависимость определяется уравнением Клапейрона – Клаузиуса (здесь X – мольная доля газа в растворе, λ – тепловой эффект растворения 1 моля газа в его насыщенном растворе):

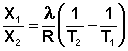(III.8)

Как правило, при растворении газа в жидкости выделяется теплота (λ < 0), поэтому с повышением температуры растворимость уменьшается. Растворимость газов в жидкости сильно зависит от концентрации других растворенных веществ. Зависимость растворимости газов от концентрации электролитов в жидкости выражается формулой Сеченова (X и X_o – растворимость газа в чистом растворителе и растворе электролита с концентрацией C):

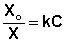(III.9)

3.1.3 Взаимная растворимость жидкостей

В зависимости от природы жидкости могут смешиваться в любых соотношениях (в этом случае говорят о неограниченной взаимной растворимости), быть практически нерастворимыми друг в друге либо обладать ограниченной растворимостью. Рассмотрим последний случай на примере системы анилин – вода. Если смешать примерно равные количества воды и анилина, система будет состоять из двух слоев жидкости; верхний слой – раствор анилина в воде, нижний – раствор воды в анилине. Для каждой температуры оба раствора имеют строго определенный равновесный состав, не зависящий от количества каждого из компонентов.

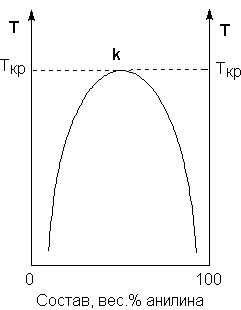
Рис. 3.1 Диаграмма растворимости системы анилин – вода

Зависимость концентрации растворов от температуры принято изображать графически с помощью диаграммы взаимной растворимости. Эта диаграмма для системы анилин-вода приведена на рис. 3.1. Область под кривой – это область расслаивания жидкостей. Повышение температуры приводит к увеличению концентрации каждого из растворов (увеличению взаимной растворимости), и при некоторой температуре, называемой критической температурой расслоения (Т_кр на рис. 3.1) взаимная растворимость воды и анилина становится неограниченной. Система анилин – вода относится к т.н. системам с верхней критической температурой расслоения; существуют также и системы, для которых повышение температуры приводит к уменьшению взаимной растворимости компонентов.

3.1.4 Растворимость твердых веществ в жидкостях

Растворимость твердых веществ в жидкостях определяется природой веществ и, как правило, существенно зависит от температуры; сведения о растворимости твердых тел целиком основаны на опытных данных. Качественным обобщением экспериментальных данных по растворимости является принцип "подобное в подобном": полярные растворители хорошо растворяют полярные вещества и плохо – неполярные, и наоборот.

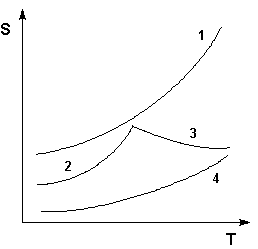
Рис. 3.2 Кривые растворимости некоторых солей в воде.
1 – КNО₃, 2 – Nа₂SО₄·10Н₂О, 3 – Nа₂SО₄, 4 – Ва(NО₃)₂
Зависимость растворимости S от температуры обычно изображают графически в виде кривых растворимости (рис. 3.2). Поскольку теплота растворения твердых веществ в жидкостях может быть как положительной, так и отрицательной, растворимость при увеличении температуры может увеличиваться либо уменьшаться (согласно принципу Ле Шателье – Брауна).

3.2 РАСТВОРЫ НЕЭЛЕКТРОЛИТОВ

3.2.1 Давление насыщенного пара разбавленных растворов

Представим, что в равновесную систему жидкость А – пар введено некоторое вещество В. При образовании раствора мольная доля растворителя X_А становится меньше единицы; равновесие в соответствии с принципом Ле Шателье – Брауна смещается в сторону конденсации вещества А, т.е. в сторону уменьшения давления насыщенного пара Р_А. Очевидно, что, чем меньше мольная доля компонента А в растворе, тем меньше парциальное давление его насыщенных паров над раствором. Для некоторых растворов выполняется следующая закономерность, называемая первым законом Рауля:

Парциальное давление насыщенного пара компонента раствора прямо пропорционально его мольной доле в растворе, причем коэффициент пропорциональности равен давлению насыщенного пара над чистым компонентом.

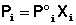(III.10)

Поскольку сумма мольных долей всех компонентов раствора равна единице, для бинарного раствора, состоящего из компонентов А и В легко получить следующее соотношение, также являющееся формулировкой первого закона Рауля:

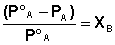(III.11)

Относительное понижение давления пара растворителя над раствором равно мольной доле растворенного вещества и не зависит от природы растворенного вещества.

Растворы, для которых выполняется закон Рауля, называют идеальными растворами. Идеальными при любых концентрациях являются растворы, компоненты которых близки по физическим и химическим свойствам (оптические изомеры, гомологи и т.п.) и образование которых не сопровождается объёмными и тепловыми эффектами. В этом случае силы межмолекулярного взаимодействия между однородными и разнородными частицами примерно одинаковы, и образование раствора обусловлено лишь энтропийным фактором. Растворы, компоненты которых существенно различаются по физическим и химическим свойствам, подчиняются закону Рауля лишь в области бесконечно малых концентраций.

3.2.2 Давление пара идеальных и реальных растворов

Если компоненты бинарного (состоящего из двух компонентов) раствора летучи, то пар над раствором будет содержать оба компонента (относительное содержание компонентов в парах будет, как правило, отличаться от содержания их в растворе – пар относительно богаче компонентом, температура кипения которого ниже). Рассмотрим бинарный раствор, состоящий из компонентов А и В, неограниченно растворимых друг в друге. Общее давление пара, согласно первому закону Рауля, равно

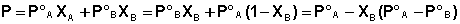(III.12)

Таким образом, для идеальных бинарных растворов зависимость общего и парциального давления насыщенного пара от состава раствора, выраженного в мольных долях компонента В, является линейной при любых концентрациях (рис.3.3). К таким системам относятся, например, системы бензол – толуол, гексан – гептан, смеси изомерных углеводородов и др.

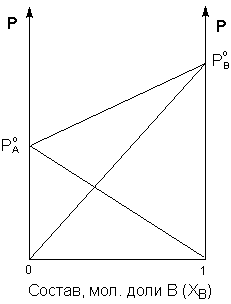
Рис. 3.3 Зависимость парциальных и общего давлений пара идеального раствора от концентрации

Для реальных растворов данные зависимости являются криволинейными. Если молекулы данного компонента взаимодействуют друг с другом сильнее, чем с молекулами другого компонента, то истинные парциальные давления паров над смесью будут больше, чем вычисленные по первому закону Рауля (положительные отклонения). Если же однородные частицы взаимодействуют друг с другом слабее, чем разнородные, парциальные давления паров компонентов будут меньше вычисленных (отрицательные отклонения). Реальные растворы с положительными отклонениями давления пара образуются из чистых компонентов с поглощением теплоты (ΔН_раств > 0), растворы с отрицательными отклонениями образуются с выделением теплоты (ΔН_раств < 0).

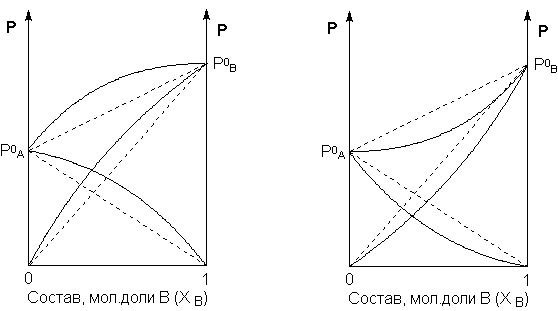
Рис. 3.4 Зависимость парциальных и общего давлений пара идеальных (штриховая линия) и реальных (сплошная линия) бинарных растворов от состава при положительных (слева) и отрицательных (справа) отклонениях от закона Рауля.

3.2.3 Температура кристаллизации разбавленных растворов

Раствор в отличие от чистой жидкости не отвердевает целиком при постоянной температуре; при некоторой температуре, называемой температурой начала кристаллизации, начинают выделяться кристаллы растворителя и по мере кристаллизации температура раствора понижается (поэтому под температурой замерзания раствора всегда понимают именно температуру начала кристаллизации). Замерзание растворов можно охарактеризовать величиной понижения температуры замерзания ΔТ_зам, равной разности между температурой замерзания чистого растворителя T°_зам и температурой начала кристаллизации раствора T_зам:

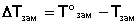(III.13)

Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис. 3.5), на которой кривая ОF есть зависимость давления пара над твердым растворителем, а кривые ОА, ВС, DE – зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно. Кристаллы растворителя будут находиться в равновесии с раствором только тогда, когда давление насыщенного пара над кристаллами и над раствором одинаково. Поскольку давление пара растворителя над раствором всегда ниже, чем над чистым растворителем, температура, отвечающая этому условию, всегда будет более низкой, чем температура замерзания чистого растворителя. При этом понижение температуры замерзания раствора ΔT_зам не зависит от природы растворенного вещества и определяется лишь соотношением числа частиц растворителя и растворенного вещества.

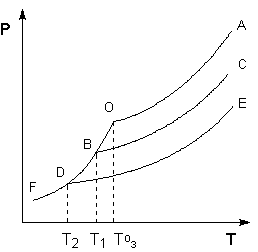
Рис. 3.5 Понижение температуры замерзания разбавленных растворов

Можно показать, что понижение температуры замерзания раствора ΔT_зам прямо пропорционально моляльной концентрации раствора:

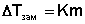(III.14)

Уравнение (III.14) называют вторым законом Рауля. Коэффициент пропорциональности K – криоскопическая постоянная растворителя – определяется природой растворителя.

3.2.4 Температура кипения разбавленных растворов

Температура кипения растворов нелетучего вещества всегда выше, чем температура кипения чистого растворителя при том же давлении. Рассмотрим Р – T диаграмму состояния растворителя и растворов различной концентрации (рис.3.5). Любая жидкость – растворитель или раствор – кипит при той температуре, при которой давление насыщенного пара становится равным внешнему давлению. Соответственно температуры, при которых изобара Р = 1 атм. пересечет кривые ОА, ВС и DE, представляющие собой зависимости давления пара над чистым растворителем и растворами с возрастающими концентрациями соответственно, будут температурами кипения этих жидкостей (рис. 3.6).

Повышение температуры кипения растворов нелетучих веществ ΔT_к = T_к – T°_к пропорционально понижению давления насыщенного пара и, следовательно, прямо пропорционально моляльной концентрации раствора. Коэффициент пропорциональности E есть эбулиоскопическая постоянная растворителя, не зависящая от природы растворенного вещества.

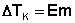(III.15)

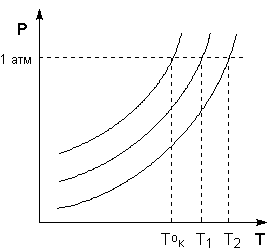
Рис. 3.6 Повышение температуры кипения разбавленных растворов

Т.о., второй закон Рауля можно в наиболее общем виде сформулировать следующим образом:

Понижение температуры замерзания и повышение температуры кипения разбавленного раствора нелетучего вещества прямо пропорционально моляльной концентрации раствора и не зависит от природы растворенного вещества.

Второй закон Рауля является следствием из первого; данный закон справедлив только для бесконечно разбавленных растворов. Коэффициенты пропорциональности в уравнениях (III.14 – III.15) – эбулиоскопическая и криоскопическая константы – имеют физический смысл соответственно повышения температуры кипения и понижения температуры замерзания растворов с моляльной концентрацией, равной 1 моль/кг. Однако, поскольку такие растворы не являются бесконечно разбавленными, эбулиоскопическая и криоскопическая константы не могут быть непосредственно определены и относятся поэтому к числу т.н. экстраполяционных констант.

3.2.5 Осмотическое давление разбавленных растворов

Если разделить два раствора с различной концентрацией полупроницаемой перегородкой, пропускающей молекулы растворителя, но препятствующей переходу частиц растворённого вещества, будет наблюдаться явление самопроизвольного перехода растворителя через мембрану из менее концентрированного раствора в более концентрированный – осмос. Осмотические свойства раствора количественно характеризуются величиной осмотического давления. Давление, которое необходимо приложить к раствору, чтобы предотвратить перемещение растворителя в раствор через мембрану, разделяющую раствор и чистый растворитель, есть осмотическое давление π. Осмотическое давление идеальных растворов линейно зависит от температуры и молярной концентрации раствора С и может быть рассчитано по уравнению (III.16):

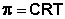(III.16)

Уравнение (III.16) есть т.н. принцип Вант-Гоффа:

осмотическое давление идеального раствора равно тому давлению, которое оказывало бы растворенное вещество, если бы оно, находясь в газообразном состоянии при той же температуре, занимало бы тот же объем, который занимает раствор.

Осмос играет важнейшую роль в процессах жизнедеятельности животных и растений, поскольку клеточная плазматическая мембрана является полупроницаемой. Осмос обусловливает поднятие воды по стеблю растений, рост клетки и многие другие явления.

Рассмотрим роль осмоса в водном режиме растительной клетки. Осмотическое давление жидкости, контактирующей с клеткой, может быть больше, меньше либо равно осмотическому давлению внутриклеточной жидкости. Соответственно выделяют гипертонические, гипотонические и изотонические растворы.

Если клетка находится в контакте с гипертоническим раствором, вода выходит из неё путём осмоса через плазматическую мембрану. Протопласт (живое содержимое клетки) при этом уменьшается в объёме, сморщивается и в конце концов отстаёт от клеточной стенки. Этот процесс называют плазмолизом. Процесс плазмолиза обычно обратим.

Если клетку поместить в чистую воду или гипотонический раствор, вода путём осмоса поступает в клетку; протопласт при этом увеличивается в объёме и оказывает давление на сравнительно жёсткую клеточную стенку. Этот процесс называется тургором. Тургорное давление препятствует дальнейшему поступлению воды в клетку. Именно тургорное давление поддерживает стебли растений в вертикальном положении, придаёт растениям прочность и устойчивость.

Изотонические растворы не оказывают влияния на водный режим клетки.

У животных клеток нет клеточной стенки, поэтому они более чувствительны к осмотическому давлению жидкости, в которой находятся. Животные клетки имеют систему защиты, основанную на осморегуляции; организм животного стремится поддерживать осмотическое давление всех тканевых жидкостей на постоянном уровне. Например, осмотическое давление крови человека – 800 000 Н/м². Такое же осмотическое давление имеет 0,9 %-ный раствор хлорида натрия. Физиологический раствор, изотоничный крови, широко применяется в медицине.

3.2.6 Понятие активности растворенного вещества

Если концентрация растворенного вещества не превышает 0.1 моль/л, раствор неэлектролита обычно считают разбавленным. В таких растворах взаимодействие между молекулами растворителя существенно преобладает над взаимодействием между молекулами растворителя и растворенного вещества, поэтому последним обычно можно пренебречь. В случае более концентрированных растворов такое приближение неправомерно и для формального учета взаимодействия частиц растворителя и растворенного вещества, а также частиц растворенного вещества между собой, вводится эмпирическая величина, заменяющая концентрацию – активность (эффективная концентрация) а, связанная с концентрацией через коэффициент активности f, который является мерой отклонения свойств реального раствора от идеального:

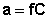(III.17)

Как правило, коэффициент активности меньше единицы (при малых концентрациях считают f = 1 и а = С). Необходимо отметить, что активность компонента не прямо пропорциональна его концентрации – коэффициент активности уменьшается с увеличением концентрации.

3.3 РАСТВОРЫ ЭЛЕКТРОЛИТОВ

3.3.1 Теория электролитической диссоциации

Законы Рауля и принцип Вант-Гоффа не выполняются для растворов (даже бесконечно разбавленных), которые проводят электрический ток – растворов электролитов. Обобщая экспериментальные данные, Я.Г. Вант-Гофф пришел к выводу, что растворы электролитов всегда ведут себя так, будто они содержат больше частиц растворенного вещества, чем следует из аналитической концентрации: повышение температуры кипения, понижение температуры замерзания, осмотическое давление для них всегда больше, чем вычисленные. Для учета этих отклонений Вант-Гофф внес в уравнение (III.16) для растворов электролитов поправку – изотонический коэффициент i:

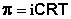(III.18)

Аналогичная поправка вносится в законы Рауля, и изотонический коэффициент определяется следующим образом:

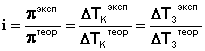(III.19)

Изотонический коэффициент для растворов электролитов всегда больше единицы, причем с разбавлением раствора i возрастает до некоторого целочисленного значения.

Для объяснения особенностей свойств растворов электролитов С. Аррениус предложил теорию электролитической диссоциации, основывающуюся на следующих постулатах:

1. Электролиты в растворах распадаются на ионы – диссоциируют;

2. Диссоциация является обратимым равновесным процессом;

3. Силы взаимодействия ионов с молекулами растворителя и друг с другом малы (т.е. растворы являются идеальными).

Диссоциация электролитов в растворе происходит под действием полярных молекул растворителя; наличие ионов в растворе предопределяет его электропроводность. Для оценки полноты диссоциации в теории электролитической диссоциации вводится понятие степень диссоциации α, которая равна отношению числа молекул n, распавшихся на ионы, к общему числу молекул N:

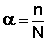(III.20)

Величина степени диссоциации зависит от природы растворителя и растворенного вещества, концентрации раствора и температуры. По величине степени диссоциации электролиты подразделяются на три группы: сильные (α ≥ 0.7), средней силы (0.3 < α < 0.7) и слабые (α ≤ 0.3). К сильным электролитам относятся почти все соли (кроме Рb(СН₃СОО)₂, НgСl₂, СdСl₂), большинство неорганических кислот и щелочей; к слабым – все органические кислоты, вода, NН₄ОН, Н₂S и т.д. Электролитами средней силы являются некоторые неорганические кислоты: НF, НСN, Н₃PO₄.

3.3.2 Слабые электролиты. Константа диссоциации

Процесс диссоциации слабых электролитов является обратимым и в системе существует динамическое равновесие, которое может быть описано константой равновесия, выраженной через концентрации образующихся ионов и непродиссоциировавших молекул, называемой константой диссоциации. Для некоторого электролита, распадающегося в растворе на ионы в соответствии с уравнением:

А_aВ_b <––> aА^x- + bВ^y+

константа диссоциации выразится следующим соотношением:

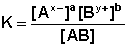(III.21)

Для бинарного (распадающегося на два иона) электролита выражение (III.21) можно переписать в виде (III.21a):

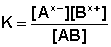(III.21a)

Поскольку концентрация каждого иона для бинарного электролита равна произведению степени диссоциации α на общую концентрацию электролита С, выражение (III.21a) в этом случае можно переписать следующим образом:

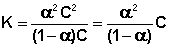(III.22)

Для разбавленных растворов можно считать, что (1 – α) = 1. Тогда получаем:

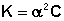(III.23) 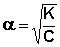(III.24)

Т.о., степень диссоциации слабого электролита обратно пропорциональна концентрации и прямо пропорциональна разбавлению раствора; выражение (III.24) называют законом разбавления Оствальда. Степень диссоциации слабого электролита можно связать с изотоническим коэффициентом. Будем считать, что из N молекул электролита продиссоциировало n молекул, образовав νn ионов (ν – число ионов, на которое диссоциирует молекула). Поскольку изотонический коэффициент показывает, во сколько раз общее число молекул и ионов в растворе больше числа молекул до диссоциации, получаем:

Дата добавления: 2014-12-07