
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Pt, H2 / 2H+ // Fe3+, Fe2+ / Pt 1 страница
|
|
|
|
Зависимость потенциала редокс-электрода εRO от концентрации (активности) окисленной [Ox] и восстановленной форм [Red] для окислительно-восстановительной реакции, в которой не участвуют никакие другие частицы, кроме окислителя и восстановителя, имеет следующий вид (здесь n – число электронов, участвующих в элементарном акте окислительно-восстановительной реакции):
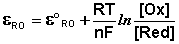 (III.54)
(III.54)
Из данного выражения следует уравнение для потенциала металлического электрода (III.40), т.к. активность атомов металла (восстановленной формы) в материале электрода равна единице.
В случае более сложных систем в выражении для окислительно-восстановительного потенциала фигурируют концентрации всех участвующих в реакции соединений, т.е. под окисленной формой следует понимать все соединения в левой части уравнения реакции
Ох + ne- ––> Red,
а под восстановленной – все соединения в правой части уравнения. Так, для окислительно-восстановительных реакций, протекающих с участием ионов водорода
Ох + ne- + mH+ ––> Red,
уравнение Нернста будет записываться следующим образом:
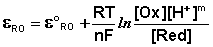 (III.55)
(III.55)
При составлении гальванических элементов с участием редокс-электрода электродная реакции на последнем в зависимости от природы второго электрода может быть либо окислительной, либо восстановительной. Например, если составить гальванический элемент из электрода Pt / Fe3+, Fe2+ и второго электрода, имеющего более положительный электродный потенциал, то при работе элемента редокс-электрод будет являться анодом, т.е. на нем будет протекать процесс окисления:
Fe2+ ––> Fe3+ + e-
Если потенциал второго электрода будет меньше, чем потенциал электрода Pt / Fe3+, Fe2+, то на последнем будет протекать реакция восстановления и он будет являться катодом:
Fe3+ + e- ––> Fe2+
Знание величин электродных потенциалов позволяет определить возможность и направление самопроизвольного протекания любой окислительно-восстановительной реакции при одновременном наличии в растворе двух или более окислительно-восстановительных пар. Восстановленная форма любого элемента или иона будет восстанавливать окисленную форму другого элемента или иона, имеющего более положительный электродный потенциал.
4.1 ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ И АДСОРБЦИЯ
4.1.1 Поверхностная энергия. Адсорбция
До сих пор свойства гетерогенных систем описывались с помощью параметров и функций состояния, характеризующих каждую из фаз в целом. Однако свойства участка фазы, примыкающего к её поверхности, отличаются от свойств фазы в объеме: фактически частицы, находящиеся на поверхности каждой фазы, образуют особую поверхностную фазу, свойства которой существенно отличаются от свойств внутренних областей фазы. Частицы, расположенные на поверхности, находятся в другом окружении по сравнению с частицами, находящимися в объеме фазы, т.е. взаимодействуют как с однородными частицами, так и с частицами другого рода. Следствием этого является то, что средняя энергия gs частицы, находящейся на поверхности раздела фаз, отличается от средней энергии такой же частицы в объеме фазы gv (причем энергия частицы на поверхности может быть как больше, так и меньше энергии частицы в объеме). Поэтому важнейшей характеристикой поверхностной фазы является поверхностная энергия Gs – разность средней энергии частицы, находящейся на поверхности, и частицы, находящейся в объеме фазы, умноженная на число частиц на поверхности N:
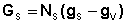 (IV.1)
(IV.1)
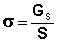 (IV.2)
(IV.2)
Очевидно, что общая величина поверхностной энергии фазы будет определяться величиной её поверхности S. Поэтому для характеристики поверхности раздела, отделяющей данную фазу от другой, вводится понятие поверхностное натяжение σ – отношение поверхностной энергии к площади поверхности раздела фаз; величина поверхностного натяжения зависит только от природы обеих фаз. Как и поверхностная энергия фазы, поверхностное натяжение может иметь как положительное, так и отрицательное значение. Поверхностное натяжение положительно, если находящиеся на поверхности частицы взаимодействуют с частицами этой же фазы сильнее, чем с частицами другой фазы (и, следовательно, gs > gv). Согласно принципу минимума свободной энергии, любая фаза будет стремиться самопроизвольно уменьшить свою поверхностную энергию; поэтому в случае положительного поверхностного натяжения (σ > 0) фаза стремится уменьшить свою поверхность. В случае если σ < 0, поверхностная энергия фазы будет уменьшаться при увеличении площади поверхности.
Влияние поверхностного слоя фазы на её общие свойства определяется долей частиц, находящихся на поверхности, от общего числа составляющих данную фазу частиц, т.е. величиной удельной поверхности фазы S/V (поверхности, приходящейся на единицу объема). Свободную энергию фазы G можно представить как сумму поверхностной Gs и объемной Gv энергий, пропорциональных соответственно площади поверхности и объему фазы:
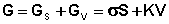 (IV.3)
(IV.3)
Разделив это выражение на объем фазы, получаем:
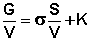 (IV.4)
(IV.4)
Из уравнения (IV.4) следует, что при одном и том же количестве фазы (т.е. неизменном объеме) вклад поверхностной энергии в общую энергию фазы возрастает с увеличением удельной поверхности или, иначе говоря, степени дисперсности (раздробленности) фазы. В случае, когда степень дисперсности фазы невелика (удельная поверхность незначительна), вкладом поверхностной энергии в полную энергию фазы обычно пренебрегают. Вклад поверхностного слоя в свойства фазы и системы в целом учитывают при изучении дисперсных систем – гетерогенных систем, одна из фаз которой является сплошной (дисперсионная среда), а другая – раздробленной (дисперсная фаза).
На границе конденсированной (т.е. твердой или жидкой) фазы с газом поверхностное натяжение всегда положительно, поскольку частицы конденсированной фазы взаимодействуют друг с другом сильнее, чем с молекулами газа. Согласно принципу минимума свободной энергии, конденсированная фаза будет стремиться самопроизвольно уменьшить свою поверхностную энергию. Это может быть результатом либо уменьшения площади поверхности фазы (именно поэтому капля жидкости в невесомости принимает форму сферы), либо уменьшения поверхностного натяжения при появлении на поверхности раздела фаз новых частиц – молекул газа либо растворенного вещества. Процесс самопроизвольного изменения концентрации какого-либо вещества у поверхности раздела двух фаз называется адсорбцией. Адсорбентом называется вещество, на поверхности которого происходит изменение концентрации другого вещества – адсорбата.
4.1.2 Адсорбция на границе раствор – пар
В жидких растворах поверхностное натяжение σ является функцией от концентрации растворенного вещества. На рис. 4.1 представлены три возможных зависимости поверхностного натяжения от концентрации раствора (т.н. изотермы поверхностного натяжения). Вещества, добавление которых к растворителю уменьшает поверхностное натяжение, называют поверхностно-активными (ПАВ), вещества, добавление которых увеличивает или не изменяет поверхностное натяжение – поверхностно-инактивными (ПИАВ).
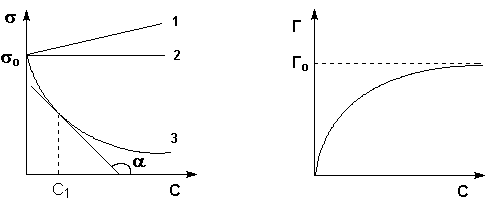
Рис. 4.1 Изотермы поверхностного Рис. 4.2 Изотерма адсорбции натяжения растворов ПАВ (1, 2) и ПАВ на границе раствор – пар ПИАВ (3)
Уменьшение поверхностного натяжения и, следовательно, поверхностной энергии происходит в результате адсорбции ПАВ на поверхности раздела жидкость – пар, т.е. того, что концентрация поверхностно-активного вещества в поверхностном слое раствора оказывается больше, чем в глубине раствора.
Количественной мерой адсорбции на границе раствор-пар является поверхностный избыток Г (гамма), равный числу молей растворенного вещества в поверхностном слое. Количественное соотношение между адсорбцией (поверхностным избытком) растворенного вещества и изменением поверхностного натяжения раствора с ростом концентрации раствора определяет изотерма адсорбции Гиббса:
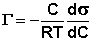 (IV.5)
(IV.5)
График изотермы адсорбции ПАВ представлен на рис. 4.2. Из уравнения (IV.5) следует, что направление процесса – концентрирование вещества в поверхностном слое или, наоборот, нахождение его в объеме жидкой фазы – определяется знаком производной dσ/dС. Отрицательная величина данной производной соответствует накоплению вещества в поверхностном слое (Г > 0), положительная – меньшей концентрации вещества в поверхностном слое по сравнению с его концентрацией в объеме раствора.
Величину g = –dσ/dС называют также поверхностной активностью растворенного вещества. Поверхностную активность ПАВ при некоторой концентрации С1 определяют графически, проводя касательную к изотерме поверхностного натяжения в точке С = С1; при этом поверхностная активность численно равна тангенсу угла наклона касательной к оси концентраций:
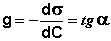 (IV.6)
(IV.6)
Нетрудно заметить, что с ростом концентрации поверхностная активность ПАВ уменьшается. Поэтому поверхностную активность вещества обычно определяют при бесконечно малой концентрации раствора; в этом случае её величина, обозначаемая gо, зависит только от природы ПАВ и растворителя. Исследуя поверхностное натяжение водных растворов органических веществ, Траубе и Дюкло установили для гомологических рядов поверхностно-активных веществ следующее эмпирическое правило:
В любом гомологическом ряду при малых концентрациях удлинение углеродной цепи на одну группу СН2 увеличивает поверхностную активность в 3 – 3.5 раза.
Для водных растворов жирных кислот зависимость поверхностного натяжения от концентрации описывается эмпирическим уравнением Шишковского:
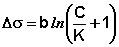 (IV.6a)
(IV.6a)
Здесь b и K – эмпирические постоянные, причём значение b одинаково для всего гомологического ряда, а величина К увеличивается для каждого последующего члена ряда в 3 – 3,5 раза.
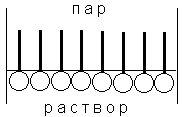
Рис. 4.3 Предельная ориентация молекул ПАВ в поверхностном слое
Молекулы большинства ПАВ обладают дифильным строением, т.е. содержат как полярную группу, так и неполярный углеводородный радикал. Расположение таких молекул в поверхностном слое энергетически наиболее выгодно при условии ориентации молекул полярной группой к полярной фазе (полярной жидкости), а неполярной – к неполярной фазе (газу или неполярной жидкости). При малой концентрации раствора тепловое движение нарушает ориентацию молекул ПАВ; при повышении концентрации происходит насыщение адсорбционного слоя и на поверхности раздела фаз образуется слой "вертикально" ориентированных молекул ПАВ (рис. 4.3). Образование такого мономолекулярного слоя соответствует минимальной величине поверхностного натяжения раствора ПАВ и максимальному значению адсорбции Г (рис. 4.1-4.2); при дальнейшем увеличении концентрации ПАВ в растворе поверхностное натяжение и адсорбция не изменяются.
1.3 Адсорбция на границе твердое тело – газ
При адсорбции газов на твердых телах описание взаимодействия молекул адсорбата и адсорбента представляет собой весьма сложную задачу, поскольку характер их взаимодействия, определяющий характер адсорбции, может быть различным. Поэтому обычно задачу упрощают, рассматривая два крайних случая, когда адсорбция вызывается физическими или химическими силами – соответственно физическую и химическую адсорбцию.
Физическая адсорбция возникает за счет ван-дер-ваальсовых взаимодействий. Она характеризуется обратимостью и уменьшением адсорбции при повышении температуры, т.е. экзотермичностью, причем тепловой эффект физической адсорбции обычно близок к теплоте сжижения адсорбата (10 – 80 кДж/моль). Таковой является, например, адсорбция инертных газов на угле.
Химическая адсорбция (хемосорбция) осуществляется путем химического взаимодействия молекул адсорбента и адсорбата. Хемосорбция обычно необратима; химическая адсорбция, в отличие от физической, является локализованной, т.е. молекулы адсорбата не могут перемещаться по поверхности адсорбента. Так как хемосорбция является химическим процессом, требующим энергии активации порядка 40 – 120 кДж/моль, повышение температуры способствует её протеканию. Примером химической адсорбции является адсорбция кислорода на вольфраме или серебре при высоких температурах.
Следует подчеркнуть, что явления физической и химической адсорбции чётко различаются в очень редких случаях. Обычно осуществляются промежуточные варианты, когда основная масса адсорбированного вещества связывается сравнительно слабо и лишь небольшая часть – прочно. Например, кислород на металлах или водород на никеле при низких температурах адсорбируются по законам физической адсорбции, но при повышении температуры начинает протекать химическая адсорбция. При повышении температуры увеличение химической адсорбции с некоторой температуры начинает перекрывать падение физической адсорбции, поэтому температурная зависимость адсорбции в этом случае имеет четко выраженный минимум (рис. 4.4).
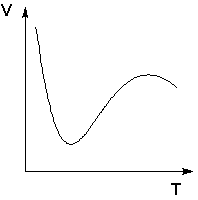
Рис. 4.4 Зависимость объема адсорбированного никелем водорода от температуры
При постоянной температуре количество адсорбированного вещества зависит только от равновесных давления либо концентрации адсорбата; уравнение, связывающее эти величины, называется изотермой адсорбции.
4.1.4 Теории адсорбции
Единой теории, которая достаточно корректно описывала бы все виды адсорбции на разных поверхностях раздела фаз, не имеется; рассмотрим поэтому некоторые наиболее распространенные теории адсорбции, описывающие отдельные виды адсорбции на поверхности раздела твердое тело – газ или твердое тело – раствор.
Теория мономолекулярной адсорбции Ленгмюра
Теория мономолекулярной адсорбции, которую разработал американский химик И. Ленгмюр, основывается на следующих положениях.
1) Адсорбция является локализованной и вызывается силами, близкими к химическим.
2) Адсорбция происходит не на всей поверхности адсорбента, а на активных центрах, которыми являются выступы либо впадины на поверхности адсорбента, характеризующиеся наличием т.н. свободных валентностей. Активные центры считаются независимыми (т.е. один активный центр не влияет на адсорбционную способность других), и тождественными.
3) Каждый активный центр способен взаимодействовать только с одной молекулой адсорбата; в результате на поверхности может образоваться только один слой адсорбированных молекул.
4) Процесс адсорбции является обратимым и равновесным – адсорбированная молекула удерживается активным центром некоторое время, после чего десорбируется; т.о., через некоторое время между процессами адсорбции и десорбции устанавливается динамическое равновесие.
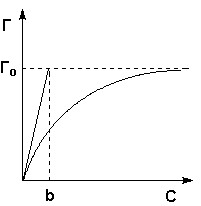
Рис. 4.5 Изотерма мономолекулярной адсорбции
В состоянии равновесия скорость адсорбции равна скорости десорбции. Скорость десорбции прямо пропорциональна доле занятых активных центров (х), а скорость адсорбции прямо пропорциональна произведению концентрации адсорбата на долю свободных активных центров (1 – х):
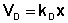 (IV.7)
(IV.7)
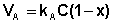 (IV.8)
(IV.8)
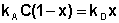 (IV.9)
(IV.9)
Отсюда находим х:
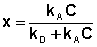 (IV.10)
(IV.10)
Разделив числитель и знаменатель правой части уравнения (IV.10) на kA, получим:
 (IV.11)
(IV.11)
Максимально возможная величина адсорбции Го достигается при условии, что все активные центры заняты молекулами адсорбата, т.е. х = 1. Отсюда следует, что х = Г / Го. Подставив это в уравнение (IV.11), получаем:
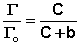 (IV.12)
(IV.12)
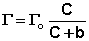 (IV.13)
(IV.13)
Уравнение (IV.13) есть изотерма мономолекулярной адсорбции, связывающая величину адсорбции Г с концентрацией адсорбата С. Здесь b – некоторая постоянная для данной пары адсорбент-адсорбат величина (отношение констант скоростей десорбции и адсорбции), численно равная концентрации адсорбата, при которой занята половина активных центров. График изотермы адсорбции Ленгмюра приведен на рис. 4.5. Константу b можно определить графически, проведя касательную к изотерме адсорбции в точке С = 0.
При описании процесса адсорбции газов в уравнении (IV.13) концентрация может быть заменена пропорциональной величиной парциального давления газа:
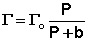 (IV.14)
(IV.14)
Теория мономолекулярной адсорбции Ленгмюра применима для описания некоторых процессов адсорбции газов и растворенных веществ при небольших давлениях (концентрациях) адсорбата.
Теория полимолекулярной адсорбции Поляни
На практике часто (особенно при адсорбции паров) встречаются т.н. S-образные изотермы адсорбции (рис. 4.6), форма которых свидетельствует о возможном, начиная с некоторой величины давления, взаимодействии адсорбированных молекул с адсорбатом.
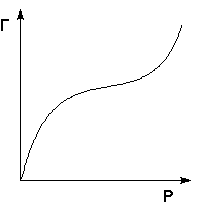
Рис. 4.6 Изотерма полимолекулярной адсорбции
Для описания таких изотерм адсорбции М. Поляни предложил теорию полимолекулярной адсорбции, основанную на следующих основных положениях:
1. Адсорбция вызвана чисто физическими силами.
2. Поверхность адсорбента однородна, т.е. на ней нет активных центров; адсорбционные силы образуют непрерывное силовое поле вблизи поверхности адсорбента.
3. Адсорбционные силы действуют на расстоянии, большем размера молекулы адсорбата. Иначе говоря, у поверхности адсорбента существует некоторый адсорбционный объём, который при адсорбции заполняется молекулами адсорбата.
4. Притяжение молекулы адсорбата поверхностью адсорбента не зависит от наличия в адсорбционном объеме других молекул, вследствие чего возможна полимолекулярная адсорбция.
5. Адсорбционные силы не зависят от температуры и, следовательно, с изменением температуры адсорбционный объем не меняется.
Уравнение Фрейндлиха
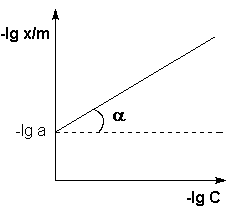
Теоретические представления, развитые Ленгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г. Фрейндлих предположил, что число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m) должна быть пропорциональна равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенной в некоторую степень, которая всегда меньше единицы:
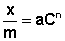 (IV.15)
(IV.15)
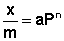 (IV.16)
(IV.16)
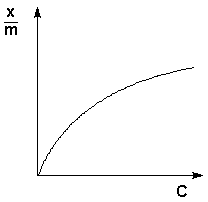 (а) (а)
|  (б) (б)
|
Рис. 4.7 Изотерма адсорбции Фрейндлиха в обычных (а) и логарифмических (б) координатах
Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения (IV.15 - IV.16), получаем:
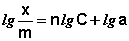 (IV.17)
(IV.17)
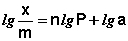 (IV.18)
(IV.18)
Т.о., зависимость логарифма удельной адсорбции от логарифма концентрации (давления) графически выражается прямой линией, отсекающей на оси ординат отрезок, равный lg a, тангенс угла наклона которой к оси абсцисс равен по величине показателю степени при давлении или концентрации (рис. 4.7):
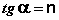 (IV.19)
(IV.19)
4.1.5 Адсорбция на границе твердое тело – раствор
Молекулярная адсорбция из растворов
Изотермы адсорбции растворенных веществ из раствора по своему виду аналогичны изотермам адсорбции для газов; для разбавленных растворов эти изотермы хорошо описываются уравнениями Фрейндлиха или Ленгмюра, если в них подставить равновесную концентрацию растворенного вещества в растворе. Однако адсорбция из растворов является значительно более сложным явлением по сравнению с газовой, поскольку одновременно с адсорбцией растворенного вещества часто происходит и адсорбция растворителя.
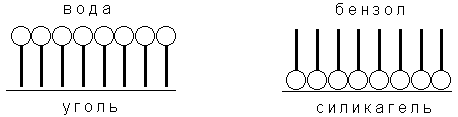
Рис. 4.8 Ориентация молекул ПАВ на поверхности адсорбента
Зависимость адсорбции от строения молекул адсорбата очень сложна, и вывести какие-либо закономерности довольно трудно. Молекулы многих органических веществ состоят из полярной (гидрофильной) и неполярной (гидрофобной) группировок, т.е. являются поверхностно-активными веществами. Молекулы ПАВ при адсорбции на твердом адсорбенте ориентируются на его поверхности таким образом, чтобы полярная часть молекулы была обращена к полярной фазе, а неполярная – к неполярной. Так, при адсорбции алифатических карбоновых кислот из водных растворов на неполярном адсорбенте – активированном угле – молекулы ориентируются углеводородными радикалами к адсорбенту; при адсорбции из бензола (неполярный растворитель) на полярном адсорбенте – силикагеле – ориентация молекул кислоты будет обратной (рис. 4.8).
Адсорбция из растворов электролитов
Адсорбция из водных растворов электролитов происходит, как правило, таким образом, что на твердом адсорбента из раствора адсорбируются преимущественно ионы одного вида. Преимущественная адсорбция из раствора или аниона, или катиона определяется природой адсорбента и ионов. Механизм адсорбции ионов из растворов электролитов может быть различным; выделяют обменную и специфическую адсорбцию ионов.
Обменная адсорбция представляет собой процесс обмена ионов между раствором и твердой фазой, при котором твердая фаза поглощает из раствора ионы какого-либо знака (катионы либо анионы) и вместо них выделяет в раствор эквивалентное число других ионов того же знака. Обменная адсорбция всегда специфична, т.е. для данного адсорбента к обмену способны только определенные ионы; обменная адсорбция обычно необратима.
При специфической адсорбции адсорбция на поверхности твердой фазы ионов какого-либо вида не сопровождается выделением в раствор эквивалентного числа других ионов того же знака; твердая фаза при этом приобретает электрический заряд. Это приводит к тому, что вблизи поверхности под действием сил электростатического притяжения группируется эквивалентное число ионов с противоположным зарядом, т.е. образуется двойной электрический слой. Взаимодействие концентрирующихся на поверхности зарядов приводит к понижению поверхностной энергии системы. Для случая специфической адсорбции электролита Песковым и Фаянсом было сформулировано следующее эмпирическое правило (правило Пескова – Фаянса):
На поверхности кристаллического твердого тела из раствора электролита специфически адсорбируется ион, который способен достраивать его кристаллическую решетку или может образовывать с одним из ионов, входящим в состав кристалла, малорастворимое соединение.
4.2 КОЛЛОИДНЫЕ СИСТЕМЫ
Коллоидные системы относятся к дисперсным системам – системам, где одно вещество в виде частиц различной величины распределено в другом (см. разд. 4.1). Дисперсные системы чрезвычайно многообразны; практически всякая реальная система является дисперсной. Дисперсные системы классифицируют прежде всего по размеру частиц дисперсной фазы (или степени дисперсности); кроме того, их разделяют на группы, различающиеся по природе и агрегатному состоянию дисперсной фазы и дисперсионной среды.
Если дисперсионной средой является жидкость, а дисперсной фазой – твердые частицы, система называется взвесью или суспензией; если дисперсная фаза представляет собой капельки жидкости, то систему называют эмульсией. Эмульсии, в свою очередь, подразделяют на два типа: прямые, или "масло в воде" (когда дисперсная фаза – неполярная жидкость, а дисперсионная среда – полярная жидкость) и обратные, или "вода в масле" (когда полярная жидкость диспергирована в неполярной). Среди дисперсных систем выделяют также пены (газ диспергирован в жидкости) и пористые тела (твердая фаза, в которой диспергированы газ либо жидкость). Основные типы дисперсных систем приведены в табл.1.
По степени дисперсности выделяют обычно следующие классы дисперсных систем:
Грубодисперсные системы – системы, размер частиц дисперсной фазы в которых превышает 10-7 м.
Коллоидные системы – системы, размер частиц дисперсной фазы в которых составляет 10-7 – 10-9 м. Коллоидные системы характеризуются гетерогенностью, т.е. наличием поверхностей раздела фаз и очень большим значением удельной поверхности дисперсной фазы. Это обусловливает значительный вклад поверхностной фазы в состояние системы и приводит к появлению у коллоидных систем особых, присущих только им, свойств.
Иногда выделяют молекулярно(ионно)-дисперсные системы, которые, строго говоря, являются истинными растворами, т.е. гомогенными системами, поскольку в них нет поверхностей раздела фаз.
Коллоидные системы, в свою очередь, подразделяются на две группы, резко отличные по характеру взаимодействий между частицами дисперсной фазы и дисперсионной среды – лиофобные коллоидные растворы (золи) и растворы высокомолекулярных соединений (ВМС), которые ранее называли лиофильными коллоидами. К лиофобным коллоидам относятся системы, в которых частицы дисперсной фазы слабо взаимодействуют с дисперсионной средой; эти системы могут быть получены только с затратой энергии и устойчивы лишь в присутствии стабилизаторов.
Растворы ВМС образуются самопроизвольно благодаря сильному взаимодействию частиц дисперсной фазы с дисперсионной средой и способны сохранять устойчивость без стабилизаторов. Лиофобные коллоиды и растворы ВМС различаются также и структурой частиц, составляющих дисперсную фазу. Для лиофобных коллоидов единицей структуры является сложный многокомпонентный агрегат переменного состава – мицелла, для растворов ВМС – макромолекула.
Таблица 1. Основные типы дисперсных систем
| Дисперсная фаза | Дисперсионная среда | Условное обозначение | Примеры дисперсных систем |
| Жидкость | Газ | ж/г | Туман, облака, жидкие аэрозоли |
| Твердое тело | Газ | т/г | Дым, пыль, твердые аэрозоли |
| Газ | Жидкость | г/ж | Пены, газовые эмульсии |
| Жидкость | Жидкость | ж/ж | Эмульсии (молоко, латекс) |
| Твердое тело | Жидкость | т/ж | Суспензии, коллоидные растворы, гели, пасты |
| Газ | Твердое тело | г/т | Твердые пены, пористые тела (пенопласты, силикагель, пемза) |
| Жидкость | Твердое тело | ж/т | Жемчуг, опал |
| Твердое тело | Твердое тело | т/т | Цветные стекла, сплавы |
4.2.1 Методы получения лиофобных коллоидов
Коллоидные системы по степени дисперсности занимают промежуточное положение между истинными растворами (молекулярно- или ионно-дисперсными системами) и грубодисперсными системами. Поэтому коллоидные растворы могут быть получены либо путем ассоциации (конденсации) молекул и ионов истинных растворов, либо дальнейшим раздроблением частиц дисперсной фазы грубодисперсных систем.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1099; Нарушение авторских прав?; Мы поможем в написании вашей работы!