Вероятность и информация

Пример 4.

Книга содержит 256 страниц. На каждой странице напечатано 64х48 символов. Можно ли записать эту книгу на гибкий магнитный диск объемом 1,44 Мб?

1. Книга содержит 256х64х48=786432 символа. Таким образом, ее информационный объем в компьютерном алфавите составляет 786432 байта.

2. 786432 байта = 786432: (1024)² = 0,75Мб.

Следовательно, книгу на данный диск записать можно.

Следует отметить, что алфавитный способ измерения информации используется для оценивания информационного объема внутренней и внешней памяти компьютера.

В разных системах передачи информации используется более точный способ измерения информации, разработанный в теории информации английским математиком Робертом Хартли и американским ученым Клодом Шенноном.

В практической жизни постоянно приходится иметь дело со случайными событиями, наступление которых предвидеть наперед трудно.

Вероятность – это числовая характеристика степени наступления случайного события при определенных условиях, отношение числа шансов, которые способствуют наступлению события, к общему числу шансов, которые способствуют или не способствуют наступлению события.

Если число шансов, которые способствуют наступлению события, , а число всех возможных шансов, которые способствуют и не способствуют наступлению события, 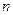, то вероятность

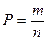(1.2)

Например, если на вечере присутствовали 37 студентов строительного факультета, 43 механика и 20 архитекторов, то вероятность встретить первого студента строительного факультета равняется 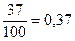, механика – 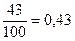, архитектора –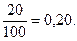

Имеет место теорема сложения вероятностей:

вероятность суммы двух независимых событий равняется сумме вероятностей этих событий, т.е. .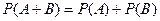

Теорема имеет два важных следствия.

Следствие 1. Если 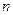рассматриваемых событий создают полную группу несовместимых событий, то сумма их вероятностей равняется 1, т.е. .

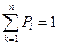Следствие 2. Если рассматривать два зависимых события, то вероятность их суммы равняется суме вероятностей этих событий без вероятности одновременного их наступления, т.е.

.

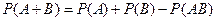Таким образом, в сумме все вероятности дают 1. Значения вероятности изменяется в пределах от 0 до 1: 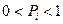. Вероятность достоверного события (события, которое обязательно совершится) равняется 1; соответственно, вероятность события, которое никогда не наступит, равняется 0. Например, вероятность того, что зима наступит после осени, равняется 1, а вероятность события, что в феврале 30 дней, – 0.

Какая связь существует между вероятностью и информацией? Информация и вероятность соединены между собой обратной связью. Чем меньше вероятность некоторого события, тем больше информации содержится в сообщении, что оно состоялось. Например, сообщение, что после 23 августа наступит 24 августа (День независимости Украины), не содержит никакой информации, поскольку в этом сообщении вероятность равняется 1 (это достоверное событие); но если сообщают, что этот день четверг, то вероятность 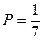, поскольку неделя имеет 7 дней, и это сообщение уже содержит определенное количество информации. Реализация менее вероятного события, т.е. большая возможность выбора, дает больше информации. Таким образом, чем больше неопределенность до получения сообщения о событии, меньше вероятность его наступления, тем больше количество информации при получении сообщения.

Проблемы измерения информации изучаются специальным разделом информатики (теория информации) – информметрии. Есть много подходов для решения этой проблемы. Одним из наиболее распространенных и практично приспособленных является вероятностный подход, идеи которого заложил английский ученый Роберт Хартли (1927-1928 гг.), а обобщил и развил американский ученый Клод Шеннон (1948-1949 гг.).

Дата добавления: 2014-12-07