Измерение количества информации по К.Шеннону

Пример 6.

Пример 5.

Сколько битов информации несет сообщение о том, что студент 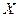живет в 90-квартирном доме?

.

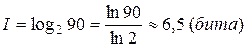Поскольку всех состояний системы - 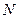и все они равновероятны, то вероятность случайного появления какого-нибудь из них 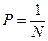, отсюда 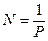. Подставив это в формулу (1.6), получим:

. (1.7)

Сколько битов информации несет сообщение о том, что вероятность появления любого из 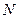состояний системы ?

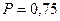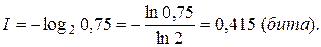
Концепцию выбора Хартли развил и обобщил из вероятностных позиций американский ученый Клод Шеннон. Он создал в 1948-1949 гг. основы статистической теории информации, основным понятием которой является энтропия. Энтропия в теории информации – мера неопределенности, которая существует при принятии сообщений. Название свое мера неопределенности получила благодаря формальной схожести с термодинамической энтропией, но суть этих понятий совсем разная. Согласно с исходными «положениями» статистической теории информации, любое сообщение, которое необходимо передать, является результатом случайного выбора из совокупности возможных сообщений данного типа. Для получателя сообщения в связи со случайностью выбора существует неопределенность, которая снимается только после получения сообщения. Мера неопределенности для получателя сообщения зависит от того, насколько большим есть выбор из возможного набора сообщений. Информация по Шеннону – это сообщение, которое уменьшает неопределенность системы (явления), которая существовала до получения сообщения. Меру этой неопределенности Шеннон и назвал энтропией.

Содержание энтропии состоит в том, что увеличение энтропии означает уменьшение упорядоченности системы. Беспорядочной система кажется тогда, когда про нее очень мало известно. Энтропия такой системы высока. С получением новых знаний о ней, с получением определенной информации, энтропия системы уменьшается. Таким образом, получение информации способствует уменьшению энтропии, причем это уменьшение пропорционально информации, которая поступает. Следовательно, за меру информации можно взять определенное количество энтропии, которая соответствует этой информации.

По Шеннону количество информации в сообщении равняется

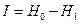(1.8)

где Н₀ – энтропия до получения сообщения, а Н₁ – энтропия после получения сообщения. Следует отметить, что Шеннон практически не делает разницы между энтропией и количеством информации. Основоположник кибернетики американский ученый Н.Винер писал, что количество информации, по сути, - некоторая неотъемлемая энтропия.

Дата добавления: 2014-12-07