Пример 8. Рассмотрим систему, которая содержит 128 клавиш – символов букв, цифр, математических и служебных знаков

Пример 7.

Рассмотрим систему, которая содержит 128 клавиш – символов букв, цифр, математических и служебных знаков. Максимальное количество информации, которую создает эта система, во время нажатия одной клавиши, равняется максимальной энтропии при равномерной частоте нажатия любой клавиши.

.

Допустим, что поступило сообщение: «нажата клавиша управления курсором». Таких клавиш всего 4 и вероятность нажатия каждой из этих клавиш одинакова. После сообщения энтропия системы Тогда, согласно формулы Шеннона (1.8)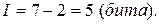

На факультете 875 студентов, среди них 247 студента-разрядника. Какое количество информации принесло сообщение «кубок по волейболу завоевала команда из 8-ми студентов-разрядников»?

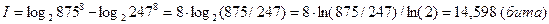Энтропия системы до получения сообщения (по теореме 1 в алфавите мощностью 875 можно построить ровно 875⁸ слов длиною 8). Энтропия системы после получения сообщения . Следовательно, . Данное сообщение несет 14,6 бита информации.

Формула Шеннона (мера Шеннона).

Базируясь на вероятностном подходе к оцениванию информации, К.Шеннон в 1948 году вывел формулу, которая дает оценку информации, абстрагируясь от ее содержания:

(1.9)

где 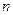- число состояний системы, 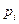- вероятность, или относительная частота перехода системы в -ое состояние, 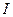- количество информации в битах, которую дает, в среднем, появление одного из 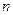разновероятных состояний системы. Таким образом,

.

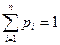Формулу Шеннона можно получить на основе следующего мыслительного эксперимента. Пусть есть программа-генератор, которая на экране дисплея может демонстрировать любую букву некоторого алфавита, который состоит из 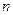букв.

ai	a1	a2	a3	...	an
pi	p1	p2	p3	...	pn

Генерирование осуществляется соответственно заданным законам распределения. Каждая из букв появляется на экране согласно с вероятностью ее появления p_i. За экраном дисплея ведется наблюдение: пусть на экране появилось m букв (m – довольно большое число, значительно больше чем 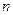). Если интересует буква a_i, то она на экране появится приблизительно 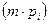раз. Каждое появление на экране буквы a_i дает по формуле (1.7) количество информации, которая равняется 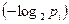, всего (за все ее появления) на экране будет получено 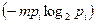битов информации. Общее количество информации, которое необходимо просуммировать после демонстрации всех m букв, равняется

.

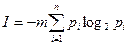На одну букву в среднем приходится:

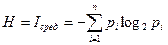(1.10)

Из этой формулы, как частный случай, получается формула Хартли (1.6). Действительно, если каждое состояние системы является равновероятным, т.е. , то энтропия системы будет максимальной и равняется: .

Дата добавления: 2014-12-07