
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Гомори
|
|
|
|
Задача целочисленного линейного программирования
Определение 9.1. Дискретное программирование – раздел математического программирования, изучающий экстремальные задачи, в которых на искомые переменные налагается условие дискретности, а область допустимых решений конечна.
Если управляющие переменные в ЗЛП определяют количество единиц неделимой продукции, то оптимальное решение должно быть получено в целых числах. Такие задачи называются ЗЦЛП. Целочисленное программирование является частным случаем дискретного.
К ЗЦЛП относится большое число экономических задач. Например, распределение производственных заказов между предприятиями, оптимальный раскрой материалов, определение загрузки оборудования, распределение транспортных средств по рейсам, задачи производства и реализации неделимой продукции.
ЗЦЛП может быть сформулировано следующим образом: найти максимум или минимум функции 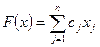 при условиях
при условиях 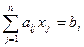
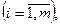

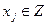 ,
,  .
.
В некоторых случаях последнее условие распространяется только на часть переменных. Такие задачи называют частично целочисленными.
Для решения ЗЦЛП разработаны специальные методы: метод сечений (метод Гомори) и метод ветвей и границ.
Алгоритм метода:
1) Отбрасывается условие целочисленности и полученная ЗЛП решается симплекс-методом.
2) Если оптимальное решение ЗЛП удовлетворяет ограничению целочисленности, то оно и является решением исходной задачи.
3) Если оптимальное решение ЗЛП не удовлетворяет ограничению целочисленности, то к основным ограничениям добавляется новое линейное ограничение, обладающее следующими свойствами:
а) оптимальный нецелочисленный план задачи ему не удовлетворяет;
б) любой целочисленный план задачи ему удовлетворяет.
4) Решается расширенная задача.
5) Процесс повторяется до получения целочисленного решения.
Определение 9.2. Дополнительное ограничение  , где фигурные скобки означают дробную часть соответствующего числа, называется сечением Гомори, а метод Гомори – методом сечения.
, где фигурные скобки означают дробную часть соответствующего числа, называется сечением Гомори, а метод Гомори – методом сечения.
Задача. Контейнер объемом 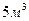 помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
помещен на контейнеровоз грузоподъемностью 12т. Контейнер требуется заполнить грузом двух наименований. Масса единицы груза, объем единицы груза, стоимости приведены в таблице:
| Вид груза | 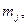 т т
| 
|  ден.ед. ден.ед.
|
Требуется загрузить контейнеровоз таким образом, чтобы стоимость перевозимого груза была максимальной.
Решим задачу методом Гомори.
Введем обозначения: х 1 – количество груза первого вида, х 2 – количество груза второго вида. Тогда экономико-математическая модель задачи примет вид:

 .
.
Преобразуем математическую модель ЗЛП без учета целочисленности переменных к допустимому предпочтительному виду канонической формы:
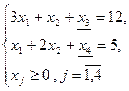
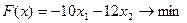 .
. 
По алгоритму основного симплекс-метода заполним симплексную таблицу решения ЗЛП:
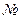
| 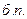
| 
| 
| 
| 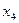
| 
|
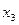
| ||||||
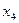 * *
| ||||||

| -10 | -12* | ||||
 * *
| 5/2 | -1/2 | 19/2 | |||

| 1/2 | 1/2 | 5/2 | |||

| -4* | -30 | ||||

| 2/5 | -1/5 | 19/5 | |||

| -1/5 | 3/5 | 3/5 | |||

| 8/5 | 26/5 | -226/5 |
Оптимальное решение ЗЛП не удовлетворяет ограничению целочисленности, следовательно, к основным ограничениям необходимо добавить новое линейное ограничение.
Замечание 9.1. Если имеется несколько дробных  , то для той у которой дробная часть больше всего составляется ограничение.
, то для той у которой дробная часть больше всего составляется ограничение.
Составим сечение Гомори для первого ограничения оптимальной симплекс-таблицы решения ЗЛП (так как  ):
):
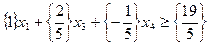 ,
,
иначе
 .
.
Преобразуем полученное ограничение к канонической форме с предпочтительной переменной:
 .
.
Продолжим решение задачи двойственным симплекс-методом, включив новое ограничение в оптимальную симплекс-таблицу решения ЗЛП:
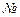
| 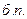
| 
| 
| 
| 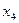
| 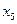
| 
|

| 2/5 | -1/5 | 19/5 | ||||

| -1/5 | 3/5 | 3/5 | ||||
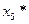
| -2/5 | -4/5 | -4/5 | ||||

| 8/5* | 26/5 | -226/5 | ||||

| |||||||

| |||||||
| -5/2 | ||||||

| -42 |
Оптимальное решение расширенной ЗЛП удовлетворяет ограничению целочисленности.
Ответ:  ,
,  .
.
Таким образом, контейнер надо загрузить 3 ед. груза первого вида и 1 ед. второго вида, при этом стоимость перевозимого груза максимальна и равна 42 ден. ед.
Замечание 9.2. Если в процессе решения получена оптимальная таблица, в которой вспомогательная переменная имеет положительное значение, то соответствующая строка может быть вычеркнута.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 1162; Нарушение авторских прав?; Мы поможем в написании вашей работы!