Общая постановка задачи динамического программирования

Задача квадратического программирования

Задача выпуклого программирования

Пусть дана система неравенств вида:

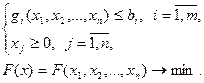
причем все функции 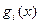являются выпуклыми на некотором выпуклом множестве М, а функция 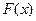либо выпукла вверх (выпукла), либо выпукла вниз (вогнута) на множестве М. 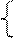ЗВП состоит в отыскании такого решения системы ограничений, при котором выпуклая функция 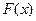достигает минимального значения, или вогнутая функция 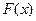достигает максимального значения.

Определение 10.1. Точка (x*, λ*) называется седловой точкой функции Лагранжа, если n -мерная точка x* является точкой минимума функции L (x, λ*), а m -мерная точка λ* – точкой максимума функции L (x*, λ), так что 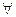x и λ выполняется неравенство:

.

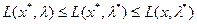Теорема 10.1. (Условие регулярности Слейтера) Множество Х допустимых решений ЗВП удовлетворяет условию регулярности Слейтера, если существует по крайне мере одно точка 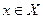, такая что .

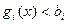Теорема 10.2 (теорема Куна-Таккера). Чтобы точка x* была оптимальным решением ЗВП, множество допустимых решений которой обладают свойством регулярности Слейтера, необходимо и достаточно, чтобы существовала такая пара (x*, λ*), которая являлась бы седловой точкой функции Лагранжа данной ЗВП.

Замечание 10.1. Если ограничения задачи – линейные функции, то выполнение условия регулярности не требуется.

Для того чтобы найти седловые точки необходимо и достаточно составить систему:

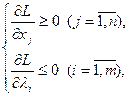
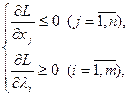
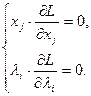
Одним из частных видов ЗВП является задача, в которой целевая функция содержит квадратичное слагаемое, а ограничения носят линейный характер. Такая задача относиться к квадратичному программированию.

В качестве основной в квадратичном программировании рассматривается задача минимизации функции

,

при ограничениях .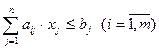

Далее будем считать, что решаемая задача квадратичного программирования является частным случаем ЗВП.

Функция Лагранжа в данном случае имеет вид:

.

Найдем стационарные точки функции Лагранжа:

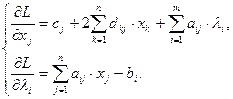
С учетом ориентации и применяя теорему Куна-Таккера:

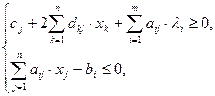(10.1)

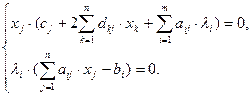(10.2)

Преобразуем систему (10.1) к системе уравнений:

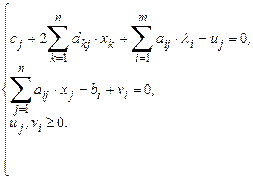
Отсюда:

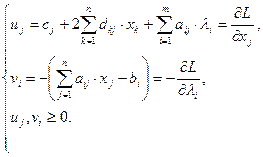
Тогда систему уравнений (10.2) можно записать в виде:

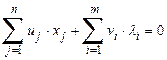. (10.3)

Чтобы учесть условие (10.3) при решении ЗНП надо следить за тем, чтобы среди базисных переменных не было u и x с одним и тем же индексом, аналогично λ и v.

Далее задача решается методом искусственного базиса.

Задача. Минимизировать функцию 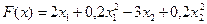при ограничениях:

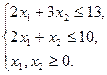
Составим функцию Лагранжа:

.

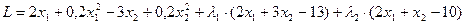Составим локальные условия Куна-Таккера:

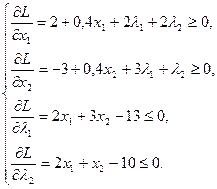
Преобразуем полученную систему ограничений к допустимому виду канонической формы:

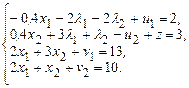
Далее решаем задачу методом искусственного базиса, учитывая условие (10.3):

N	б.п.	x1	x2	λ1	λ 2	u1	u2	v1	v2	z	b
	u1	-0,4		-2	-2
z		0,4				-1
v1*
v2
G		-0,4*	-3	-1
	u1	-0,4		-2	-2
z*	-4/15					-1	-2/15			19/15
x2	2/3						1/3			13/3
v2	4/3						-1/3			17/3
G	41/5		-3*	-1			2/15			19/15
	u1										128/45
λ1	-4/45			1/3		-1/3	-2/45		1/3	19/45
x2	2/3						1/3			13/3
v2	4/3						-1/3			17/3
G

Получили оптимальный план решения задачи 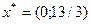. Найдем значение целевой функции в данной точке:

.

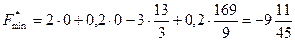Ответ: , .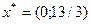

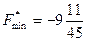Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение использовать аналитические методы решения задач математического программирования при наличии нелинейных функциональных зависимостей экономических переменных.

Тема 11. Метод динамического программирования

План лекции:

1. Общая постановка задачи динамического программирования (ЗДП)

2. Принцип оптимальности. Функциональные уравнения Беллмана

3. Задача оптимального распределения инвестиций

4. Задача о замене оборудования

Определение 11.1. Динамическое программирование – это метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми.

Многие экономические процессы расчленяются на шаги естественным образом. Например, процессы планирования и управления, развиваемые во времени. Здесь естественный шаг: год, квартал, месяц и т.д.

Рассматриваемые ранее задачи (ЗЛП и ЗНП) относятся к задачам однократного принятия решений, ЗДП требует некоторой последовательности принятых решений и относится к многоэтапным (многошаговым) задачам.

Если модели линейного программирования можно использовать в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели динамического программирования применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию и т.д.

В общем случае ЗДП формулируется следующим образом: имеется некоторая управляемая система S, характеризующаяся определенным набором параметров, задающих ее состояние, которая под влиянием управления переходит из начального состояния в конечное.

Состояние системы на каждом шаге определяется вектором-состояния 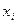. Дальнейшее изменение ее состояния зависит только от данного состояния и не зависит от того, каким путем система перешла в него (процесс без последействия).

На каждом шаге выбирается одно решение 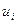(управление), под действием которого система переходит из предыдущего состояния 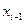в новое 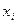. Это новое состояние является функцией состояния на начало шага 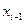и принятого в начале решения 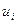, то есть .

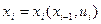Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью) или потерей (издержками), которые зависят от состояния на начало шага и принятого решения:

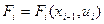– приращение целевой функции в результате i -го шага и принятого решения:

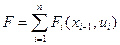– значение целевой функции при переходе системы из начального состояния в конечное за n шагов.

На векторы-состояния и управления могут быть наложены ограничения, объединение которых составляет область допустимых решений .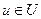

Требуется найти такое допустимое управление 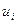для каждого шага, чтобы получить экстремальное значение целевой функции за все n шагов.

Определение 11.2. Любую допустимую последовательность действий для каждого шага, переводящую систему из начального состояния в конечное, называют стратегией управления. Допустимая стратегия управления, при которой целевая функция принимает экстремальное значение, называется оптимальной.

Дата добавления: 2014-12-07