Артиллерийского оружия. Газоотводного двигателя автоматики

Газоотводного двигателя автоматики

Математическая модель работы

Для анализа физических явлений в газоотводном двигателе и практического решения задачи определения давления в цилиндре двигателя принимаются следующие допущения:

– состояние газа в цилиндре двигателя считается стационарным, а течение газов в канале и в зазоре – подчиняющимся законам стационарного истечения;

– тепло, вносимое газами в цилиндр двигателя, расходуется только на изменение внутренней энергии газа и на совершение работы при перемещении поршня;

– теплофизические характеристики газа принимаются постоянными.

При этих допущения процессы в газоотводном двигателе автоматики оружия описываются следующей системой дифференциальных уравнений.

Уравнение сохранения энергии. Изменение тепловой энергии газа в двигателе автоматики идет на изменение внутренней энергии газа и на совершение работы

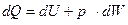, (2.15)

где dQ – изменение тепла газа;

dU – изменение внутренней энергии газа;

dW – изменение объема цилиндра двигателя.

Изменение тепла газа в период течения его из ствола в цилиндр (увеличение) будет равно подводимому теплу, за вычетом потерь на утечку и потерь на нагрев цилиндра двигателя автоматики

, (2.16)

где 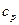– теплоемкость газа при постоянном давлении;

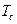– температура газа в стволе;

Т – температура газа в цилиндре двигателя;

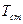– температура стенок цилиндра;

G_f – весовой расход газа из ствола через отверстие сечением f;

G_j – весовой расход газа из цилиндра через зазор площадью j

a – коэффициент теплоотдачи;

F – площадь, поверхности охлаждения цилиндра.

При обратном течении газа из цилиндра двигателя в ствол изменение тепла газа (уменьшение) можно определить по формуле

, (2.17)

где – массовый расход газа из цилиндра в ствол через отверстие сечением f.

Внутренняя энергия газа, находящегося в цилиндре, определяется уравнением его состояния

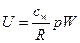. (2.18)

Тогда изменение внутренней энергии этого газа можем записать в виде

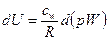. (2.19)

Второе слагаемое в уравнении (2.15) определяющее совершаемую пороховыми газами работу, найдем из уравнения

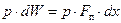, (2.20)

где – площадь поршня; dx – элементарное перемещение поршня.

Подставляя в уравнение (2.15) выражения (2.16), (2.19) и (2.20), после преобразования получим

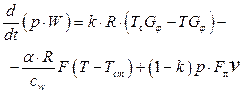(2.21)

где 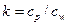– отношение теплоемкостей;

– скорость поршня.

Для периода обратного течения газа с учетом выражения (2.17) получим уравнение вида

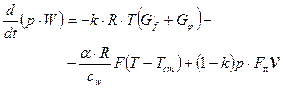(2.22)

Уравнение изменения массы газа в цилиндре двигателя за время dt можно записать в виде

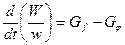, (2.23)

где w – удельный массовый объем газа в цилиндре.

Для периода обратного течения газа уравнение соответственно запишем в виде

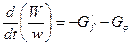. (2.24)

Уравнение движения поршня составим в предположении, что сила сопротивления равна П, а масса поршня постоянна и равна М, в виде

. (2.25)

Для решения полученных выше уравнений введем следующие очевидные уравнения:

- изменения рабочего объема газового цилиндра двигателя

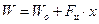, (2.26)

- скорость перемещения поршня выразим через его перемещение

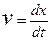, (2.27)

- изменение площади, поверхности охлаждения цилиндра двигателя автоматики

, (2.28)

- состояния газа

. (2.29)

В данных уравнениях:

– начальный объем цилиндра;

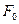– начальная площадь поверхности охлаждения цилиндра двигателя;

D – диаметр цилиндра;

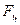– площадь поперечного сечения газового цилиндра.

В результате решения полученной системы уравнений (2.21-2.29) определяются характеристики двигателя автоматики оружия в функции времени, а именно: давление газов, скорость поршня, площадь поверхности охлаждения его стенок, удельный объем газа, температура газа и рабочий объем цилиндра ().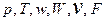

При решении системы уравнений следует иметь в виду, что ее нужно интегрировать по участкам, соответствующим различным режимам истечения газа. Переход от одного участка к другому определяется как изменением направления истечения газа в газоотводном отверстии ствола, так и соотношением давлений в стволе и цилиндре двигателя.

Система уравнений (2.21-2.29) замкнутая. Ее интегрирование с помощью ЭВМ не вызывает трудностей. Вместе с тем существует более простой приближенный метод определения давления пороховых газов на поршень двигателя автоматики оружия, разработанный И.Е. Цибулевским [1,2].

Дата добавления: 2014-12-27