Расчет ствола на прочность

Во время стрельбы стенки ствола деформируются в результате давления на них пороховых газов, скручиваются и растягиваются в результате воздействия ведущего пояска на боевые грани нарезов, растягиваются силами трения снаряда о поверхность канала ствола и инерционными усилиями, возникающими при откате ствола, наконец, они нагреваются пороховыми газами.

Решающее влияние на прочность ствола оказывает давление пороховых газов. Поэтому расчет ствола на прочность обычно ведется только на внутреннее давление пороховых газов, а остальные воздействия учитывают за счет некоторого запаса прочности.

При расчете ствола на прочность обычно принимают следующие допущения:

1. Ствол считается цилиндрическим, а имеющиеся конические участки разбиваются на необходимое число цилиндрических так, чтобы разница в диаметрах оснований была не значительной;

2. Пренебрегают силами инерции элементов ствола, осевыми и скручивающими усилиями, поскольку их влияние незначительно;

3. Температурные напряжения и снижение допустимых напряжений вследствие нагревания ствола учитываются при специальных расчетах. Основной расчет проводят для первого выстрела;

4. Материал ствола считают однородным;

5. Ствол после деформации сохраняет цилиндрическую форму и любое его сечение остается плоским;

6. Давление в стволе действует статически.

С учетом этих допущений задача расчета ствола на прочность сводится к определению напряжений в толстостенной трубе, подверженной внутреннему давлению, т.е. к известной в теории упругости задаче Ламе-Гадолина.

В результате для определения напряжений в стенке ствола можно использовать следующие формулы:

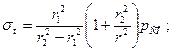(2.8)

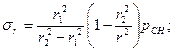(2.9)

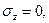
где 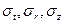– соответственно тангенциальное, радиальное и осевое напряжения;

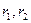– радиусы внутренней и наружной поверхностей ствола;

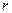– текущий радиус по толщине стенки ствола ().

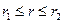Анализ этих формул позволяет сделать следующие выводы:

- тангенциальное напряжение является растягивающим, а радиальные – сжимающими ();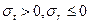

-
тангенциальные напряжения всегда больше радиальных и достигают максимальных значений на внутренней поверхности ствола ();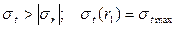

- максимальное тангенциальное напряжение всегда больше внутреннего давления (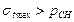), т.е. без принятия специальных мер нельзя изготовить ствол, выдерживающий давление, равное пределу прочности внутренних слоев ствола.

Увеличение прочности ствола по отношению к внутреннему давлению достигается за счет изготовления многослойных и автофретированных стволов. В многослойных стволах наружная труба надевается на внутреннюю с некоторым натягом. Вследствие натяга тангенциальные напряжения в стенке внутренней трубы уменьшаются, а в стенке наружной трубы увеличиваются. В автофретированных (или многослойных автоскрепленных) стволах предварительное напряжение во внутренних слоях стенки ствола получают, подвергая их большому внутреннему давлению, при котором эти слои получают пластическую деформацию. Увеличение прочности этих слоев происходит за счет образования наклепа металла и появления остаточных напряжений сжатия.

Во время выстрела каждый элемент ствола испытывает сложное напряженное состояние. В этом случае для определения прочности ствола необходимо воспользоваться одной из теорий прочности. Наибольшее распространение при расчете стволов получила теория наибольших относительных деформаций. В основу этой теории положено допущение о том, что прочность материала не нарушается, если наибольшая относительная деформация при сложном напряжении достигает такого значения, которое имеет место при простом нагружении с допускаемым напряжением растяжения или сжатия.

Величина относительной деформации 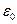при простом нагружении (сжатие или растяжение) по допускаемому напряжению 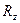определяется по формуле

,

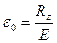где Е – модуль упругости материала ствола.

Учитывая, что максимальная относительная деформация ствола имеет место в тангенциальном направлении и ее величина определяется формулой

,

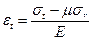для принятой теории условие обеспечения прочности (ε₀ = ε_t) выражается следующей зависимостью:

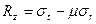, (2.10)

где 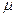– коэффициент Пуассона (для стали ).

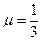Выше было показано, что максимальные напряжения возникают на внутренней поверхности ствола. Тогда подставляя в формулу (2.10) значения 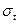и 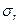из выражений (2.8, 2.9) и принимая 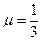, получим

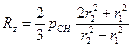. (2.11)

При расчете на прочность обычно задается некоторый запас прочности деталей

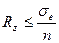, (2.12)

где 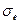– предел упругости;

n – коэффициент запаса прочности.

На практике при расчете ствола используется так называемое предельное давление 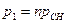. Кроме того, в расчетах учитывают, что при первых выстрелах материал ствола упрочняется, поэтому допустимые напряжения в формуле (2.12) относят не к пределу упругости 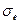, а к пределу текучести .

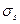Таким образом, заменяя в формуле (2.12) 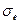на 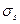и подставляя в нее значение 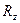из выражения (2.11), окончательно получим условие обеспечения прочности в следующем виде:

.

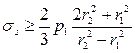Тогда для определения минимального значения наружного радиуса ствола получим формулу в виде

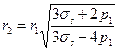. (2.13)

Расчет ствола на прочность с использованием формулы (2.13) выполняют в следующей последовательности:

§ баллистическим расчетом определяют кривую давления пороховых газов по длине ствола p (l) и значение максимального давления ;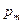

§ строят кривую предельного давления 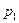(l). При этом по всей длине патронника принимают 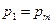, от начала соединительного конуса по длине ствола за точку максимального давления на два-три калибра предельное давление принимают постоянным значением, равным (1,1…1,2) 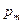, и далее к дульному срезу ;

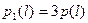§ выбирают материал ствола с определенным значением предела текучести 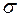_s;

§ в соответствии с формулой (2.13) рассчитывают минимальный наружный радиус ствола;

§ из конструктивных соображений окончательно выбирают конфигурацию и наружные размеры ствола так, чтобы по всей длине ствола размеры не выходили за пределы минимально допустимых.

В настоящее время стволы авиационного оружия изготовляют из стали с пределом текучести 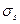=700…850 МПа.

Дата добавления: 2014-12-27