Пример 3.4

Решение

Пример 3.3.

Пример 3.2.

Для нашей компании Gamma

Год PV

Год 0: (200.000)

Год 1: 61.489

Год 2: 63.027

Год 3: 56.031

Год 4: 40.950

221.497

.

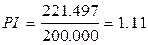Вывод: так как PI > 1, проект эффективен.

Рассчитайте динамический срок окупаемости по проекту. Денежные потоки по первым четырем годам осуществления следующие:

Годы	Денежные потоки, млн. руб.
0 (стартовые инвестиции)	-1000

Цена источников финансирования 5,5%.

Годы	Денежные потоки, млн. руб.	PV
0 (стартовые инвестиции)	-1000	-1000 473,9 359,4 255,5 80,72

DPP = m + ,

DPP = 2г. +

Вывод: проект эффективен, т.к. DPP < T (срока жизни проекта).

Инвестиционная компания получила для рассмотрения несколько инвестиционных проектов. Необходимо выбрать из них наиболее эффективные, исходя из бюджета около 130 млн дол.

Проект	Приведенные инвестиции, тыс. дол.	Приведенные поступления, тыс. дол.	PI	Рейтинг проекта	Выбор
А	10 000	24 000	2.4		+
Б			2.67		+
В			1.2
Г			0.98
Д			1.42
Е			1.5		+
Ж			1.13
З	150 000	190 000	1.27
И	120 000	175 000	1.46		+
Итого

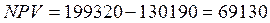тыс. дол.

Задача 3.1. Рассмотреть экономическую целесообразность реализации проекта при следующих условиях: величина инвестиций 25 млн руб., период реализации проекта – 4 года, доходы по годам – 10 000, 10 000, 12 500, 12 500 тыс. рублей, ставка дисконтирования 20%.

Задача 3.2. Машиностроительная фирма решила закупить новое оборудование. Инвестиционные затраты на приобретение – 300 тыс. марок. Срок эксплуатации оценен в 6 лет, после чего остаточная стоимость равна нулю. Ставка дисконтирования составила – 11%. Суммарная экономия ежегодных текущих затрат от установки нового оборудования (экономия сырья, заработной платы и проч.) составила 80 тыс. марок. Выгодно ли оказалось инвестирование?

Задача 3.3. Инвестор решил приобрести бензозаправочную станцию стоимостью 600 млн руб. Ежегодные, прогнозируемые в течении последующих 10 лет, свободные от долгов, поступления составят 1 300 млн рублей. В конце десятого года инвестор планирует продать станцию по цене 900 млн рублей. Ставка дисконтирования принимается на уровне минимально приемлемого для инвестора дохода и равна 140% годовых. Рассчитать чистую текущую стоимость проекта.

Методические указания:

Остаточную стоимость (R) необходимо учесть при расчете чистой текущей стоимости как приток по формуле:

,

где – остаточная стоимость;

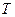– срок жизни проекта.

Задача 3.4. Инвестор решил приобрести станок стоимостью 200 млн рублей. Ежегодные прогнозируемые в течение последующих 10 лет, свободные от долгов поступления составят 140 млн руб. В конце 10 года инвестор планирует продать станок по цене 300 млн руб. Ставка дисконтирования принимается на уровне минимального приемлемого для инвестора дохода и равна 130% годовых. Требуется рассчитать чистую текущую стоимость.

Задача 3.5. Проанализировать два альтернативных проекта, если “цена” капитала компании составляет 16%. Оценку произвести по показателю чистой текущей стоимости проекта. Исходные данные следующие:

Проект	Величина инвестиций, млн руб.	Ожидаемый доход по годам, млн руб.
		1-й	2-й
		2 500	1 400   10 000

Задача 3.6. В таблице приведены исходные данные по двум альтернативным проектам. Используя показатель чистой текущей стоимости проекта, выбрать один из них при условии, что “цена” капитала, предназначенного для инвестирования: a) 11%, b) 13%.

(млн руб.)

Проект	Величина инвестиций	Ожидаемый доход по годам
1-й	2-й	3-й

Задача 3.7. В таблице приведены два альтернативных проекта:

Проект	Величина инвестиций, млн руб.	Годовые суммы денежных поступлений, млн руб.
	350 000   50 000	125 000   20 000

Срок жизни проекта - 4 года, ставка дисконтирования 12%. Оценить инвестиционную привлекательность проектов, используя показатель чистой текущей стоимости проекта.

Задача 3.8. Предположим, что Вы решили приобрести грузовой автомобиль и сдать его в аренду. Банк предоставляет Вам кредит под 32% годовых. Стоимость автомобиля 140 тыс. рублей. Планируемые ежегодные платежи от арендатора составят 60 тыс. рублей. Срок аренды 6 лет. Необходимо рассчитать чистую текущую стоимость, полученную в результате этой операции.

Задача 3.9. Компания оценивает три инвестиционные ситуации:

1) производство новой партии алюминиевых кастрюль, 2) расширение имеющегося производства печей, в том числе и печей новых размеров, 3) разработка новой высококачественной печи. Эти проекты имеют ожидаемую текущую стоимость и требуют инвестирования в объемах, показанных в таблице (с учетом всех инвестиционных налоговых кредитов):

(долл.)

Проект	Необходимый объем инвестиций	Текущая стоимость будущих денежных потоков
	200 000 115 000 270 000	290 000 185 000 400 000

Если одновременно разрабатываются проекты 1 и 2, то экономии не будет, необходимый объем инвестиций и текущая стоимость комбинации равняется сумме соответствующих показателей по проектам.

При одновременной разработке проектов 1 и 3 возможна экономия на инвестициях, поскольку один из видов приобретаемого оборудования может использоваться в обоих производственных процессах. Общий объем инвестиций, необходимый для осуществления проектов 1 и 3, равен 440 000 дол.

Если разрабатываются проекты 2 и 3, экономия может быть достигнута за счет маркетинга и производства продукции, но не за счет инвестиций. Ожидаемая текущая стоимость будущих денежных потоков при одновременной разработке проектов 2 и 3 равна 620 000 дол.

Если принять все три проекта, имеют место все упомянутые выше эффекты. Однако в этом случае понадобится затратить 125 000 дол. на расширение предприятия, поскольку его площади сейчас не позволяют одновременно разрабатывать все 3 проекта. Какой проект или проекты выбрать компании?

Задача 3.10. Предприятие рассматривает целесообразность приобретения новой технологической линии. Стоимость линии составляет 12,7 млн рублей, срок эксплуатации – 5 лет, износ на оборудование начисляется по методу прямолинейной амортизации, динамика выручки от реализации и текущих расходов представлена в таблице.

Ставка налога на прибыль составляет 24%, “цена” капитала – 20%. Целесообразен ли данный проект к реализации? Сделайте вывод, используя критерий NPV.

Показатели	Годы
1-й	2-й	3-й	4-й	5-й
Объем реализации (тыс. рублей) Текущие расходы (без амортизации) (тыс. рублей)

Методические указания:

Чистый денежный поток за период t можно рассчитать по формуле:

,

,

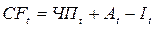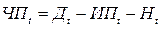где – чистая прибыль за период t;

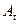– амортизационные отчисления за период;

– инвестиционные затраты;

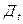– доход от продаж;

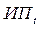– издержки производства;

– налог на прибыль.

Задача 3.11. Рассматриваются два альтернативных проекта:

А: - 50000 15625 15625 15625 15625 15625

Б: - 80000 - - - - 140000

1. Найдите точку Фишера;

2. Сделайте выбор при r=5% и при r=10%.

Задача 3. 12. Рассматриваются два альтернативных проекта:

А -100 90 45 9

Б -100 10 50 100

Требуется: 1) найти точку Фишера;

2) сделать выбор при r=8% и при r=15%.

Задача 3.13. Величина требуемых инвестиций по проекту равна $18000; предполагаемые доходы: в первый год - $1500, в последующие 8 лет – по $3600 ежегодно. Оцените целесообразность принятия проекта, если цена капитала 10%.

Задача 3.14. Акционерное общество предполагает купить швейную фабрику за 510 млн руб., сложившийся уровень рентабельности по альтернативным вложениям составляет 15%. Эта фабрика согласно расчетам способна обеспечить получение ежегодно денежных поступлений в размере 70 млн руб.

Рассчитать чистую текущую стоимость проектов для двух случаев:

а) если денежные поступления не будут возрастать;

б) если ожидаемый рост денежных поступлений составит 4% в год после того, как в конце первого года они составят 70 млн руб.

Методические указания:

Для случая, когда срок жизни не ограничен (условно-бесконечен), NPV рассчитывается по формуле Гордона:

,

где g - постоянный темп с которым будет расти ежегодно поступление

денежных средств;

d - ставка дисконтирования;

CF₁ - поступления денежных средств в конце первого года после осуществления инвестиций.

Задача 3.15. Завод по кустарному производству мороженного имеет 2 машины с производительностью 1000 штук в год каждая. Предположим, что срок жизни проекта не ограничен (стремится к бесконечности), остаточная стоимость равна нулю. Затраты на производство единицы продукции - 2 дол.

Год делится на два сезона:

- 0,5 года - высокий спрос, 100%-е использование мощностей;

- 0,5 года - низкий спрос, 50%-е использование мощностей.

Предположим, что можно купить новую машину, стоимостью 6000 дол., она более современная и затраты на производство единицы продукции составляет 1 дол. Ставка дисконтирования -10%.

Возможны три варианта:

I вариант- продолжить работать на двух машинах;

II вариант- купить одну новую и оставить одну старую;

III вариант- купить две новые, старые не использовать.

Какой вариант выгоднее?

Задача 3.16. Строительная компания по договору с муниципалитетом берется осуществить строительство дороги общей стоимостью 168 млн. у.е. за 5 лет. Согласно договору, муниципалитет оплачивает авансом 15% стоимости проекта в первый год (заранее), кроме того, оплачивает 80% счетов, из 20% оставшихся 15% идет на возмещение оплаты первого года и 5% - залог для гарантирования качества.

Для осуществления строительства компания должна купить в начале проекта (год 1) оборудование на 38 млн у. е.

Текущие затраты и выручка (счета к оплате муниципалитетом):

1998 7 11

1999 28 43

2000 31 48

2001 25 39

2002 17 27

Рассчитать чистый денежный поток и чистую текущую стоимость проекта при ставке дисконтирования 10%.

Задача 3.18. Инвестор вложил в строительство предприятия 12 млн дол. Планируемые ежегодные поступления составят:

1 год – 4 млн дол.

2 год – 6 млн дол.

3 год – 8 млн дол.

4 год – 3 млн. долларов.

Требуется определить внутреннюю норму доходности проекта.

Задача 3.19. Величина инвестиций – 1 млн руб.; прогнозная оценка генерируемого по годам дохода (тыс. руб.): 344; 395; 393; 322. Рассчитайте значения показателей IRR и MIRR, если цена капитала 10%.

Задача 3.20. Рассчитайте IRR проекта при следующих денежных потоках: -200 20 40 60 60 80

Задача 3.21. Рассчитайте IRR и MIRR проекта, если цена капитала равна 10%. Денежные потоки по годам: -1 8 -14 7

Задача 3.22. Денежные потоки двух проектов (млн руб.) следующие:

П1 -10 5 3 2 4

П2 -10 2 3 5 4

Какой критерий не делает различия между этими проектами?

Не делая специальных расчетов, ответьте на вопросы: а) одинаковы ли IRR этих проектов или нет; б) если IRR различны, какой проект имеет большее значение IRR и почему? Ответы обоснуйте.

Задача 3.23. Имеются два независимых проекта А и В, данные, о которых приведены ниже:

Проект	Денежные потоки, млн. руб.
CF	CF	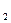CF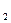
А		-150
В	-50

Можно ли их принять к реализации, если цена капитала: а) 10%; б) 30%?

Решение принять с помощью критериев IRR и NPV.

Дать графическое представление результатов.

Задача 3.24. Имеются два альтернативных проекта С и Д, данные, о которых приведены ниже:

Проект	Денежные потоки, млн. руб.
CF	CF	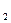CF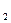
С		-150
Д	-50

Какой из них предпочтительней, если цена капитала: а) 10%; б) 50%?

Для принятия решения использовать точку Фишера.

Задача 3.25. Найдите IRR денежного потока: -100, +230, -132.

Задача 3.26. Акционерное общество в 1989 г. построило кинотеатр, затратив 200 тыс. руб. Кинотеатр принес прибыль в 1990 г. в размере 100 тыс. руб., в 1991 г. и в 1992 г. – по 1 млн руб., после чего в конце 1992 г. был продан за 5 млн руб. Оценить рентабельность инвестиций данного проекта, если ставки дисконтирования составили: в 1990 г. – 20%, в 1991 г. – 50%, в 1992 г. – 60%.

Задача 3.27. Инвестиционная компания получила для рассмотрения несколько инвестиционных проектов. Необходимо выбрать из них наиболее эффективные, исходя из бюджета около 70 000 тыс. руб.

Проект	Приведенные поступления, тыс. руб.	Приведенные инвестиции, тыс. руб.
	12 000 95 000 87 500	5 000 75 000 60 000

Задача 3.28. Фирма планирует инвестировать в основные фонды 60 млн денежных единиц. “Цена” источников финансирования – 10%. Рассматриваются четыре альтернативных проекта со следующими потоками платежей (млн денежных единиц):

Проект А: -35; 11; 16; 18; 17

Проект Б: -25; 9; 13; 17; 10

Проект В: -45; 17; 20; 20; 20

Проект Г: -20; 9; 10; 11; 11

Составить оптимальный план размещения инвестиций (возможно дробление рассматриваемых проектов).

Методические указания:

1. Для каждого проекта рассчитать индекс доходности PI.

2. Проекты проранжировать по степени убывания PI.

3. К реализации принять первые X проектов, стоимость которых в сумме не превысит лимита средств, предназначенных на инвестиции.

4. При наличии остатка инвестиционных средств они вкладываются в очередной проект, но не в полном объеме, а лишь в той части, в которой он может быть профинансирован.

Задача 3.29. Используя данные предыдущей задачи, составить план оптимального размещения инвестиций, если лимит инвестиций не должен превысить 60 млн денежных единиц, а к реализации могут быть приняты проекты только в полном объеме.

Методические указания:

Рассмотреть возможные сочетания проектов и их суммарные NPV.

Задача 3.30. По условиям задачи 3.28 составить оптимальный план размещения инвестиций на два года при условии, что инвестиции на планируемый год не могут превысить 75 млн денежных единиц.

Методические указания:

По каждому проекту рассчитать индекс возможных потерь, характеризующий относительную потерю NPV в случае, если проект будет отсрочен к исполнению на год.

Индекс рассчитывается по формуле:

,

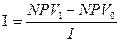где 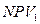– приведенная стоимость проекта в случае начала реализации проекта в текущем году;

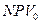– приведенная стоимость проекта в случае начала реализации проекта через год;

- размер отложенных на год инвестиций.

,

Реализацию проектов, обладающих наименьшей величиной индекса возможных потерь, перенести на следующий год.

Задача 3.31. Предприятие имеет возможность инвестировать до 60 млн руб., при этом цена источников финансирования составляет 10%. Требуется составить оптимальный инвестиционный портфель, если имеются следующие альтернативные проекты:

Проект	Денежные потоки по годам (млн руб.)
	1-й	2-й	3-й	4-й	5-й
А Б В Г	-30 -20 -40 -15

Инвестиции осуществляются в течение первого года, выпуск продукции - со второго года. Выбор осуществить на основе показателей: чистой текущей стоимости проекта, индекса доходности и внутренней нормы доходности.

Задача 3.32. Предприятие имеет возможность инвестировать:

а) до 55 млн руб.; б) до 90 млн руб., при этом цена капитала составляет 10%. Составьте оптимальный инвестиционный портфель из следующих альтернативных проектов (млн руб.):

А -30 6 11 13 12

Б -20 4 8 12 5

В -40 12 15 15 15

Г -15 4 5 6 6

Задача 3.33. Анализируются четыре проекта (тыс. долл.):

Год А Б В Г

0 -31 -60 -25 -40

1 6 20 30

2 6 20 25

3 6 40

4 6 10

5 6

6 6

7 6

8 6

9 6

10 6 80

Цена капитала – 12%. Бюджет ограничен $120000. Предполагая, что проекты независимы и делимы, составьте оптимальную комбинацию.

Задача 3.34. Объем инвестиционных возможностей компании ограничен $90000. Имеется возможность выбора из следующих шести проектов:

I IRR NPV

A -30000 13.6% 2822

B -20000 19.4% 2562

C -50000 12.5% 3214

D -10000 21.9% 2679

E -20000 15.0% 909

F -40000 15.6% 4509

Предлагаемая цена капитала 10%. Сформируйте оптимальный портфель по критериям: (а) NPV; (б) IRR; (в) PI.

Задача 3.35. Анализируются четыре проекта, причем А и В, а также Б и Г - взаимоисключающие проекты. Составьте возможные комбинации проектов и выберите оптимальную.

I NPV IRR

А - 600 65 25%

Б - 800 29 14%

В - 400 68 20%

Г - 280 30 9%

Задача 3.36. Предприятие инвестировало на строительство гостиницы 40 млн руб. Ежегодные планируемые поступления от эксплуатации гостиницы составляет соответственно 35, 60, 80 и 100 млн руб.

Ставка дисконтирования 100%. Определить статический и динамический сроки окупаемости.

Задача 3.37. Анализируются проекты (дол.):

I CF1 CF2

А. - 4000 2500 3000

Б. - 2000 1200 1500

Ранжируйте проекты по критериям IRR, DPP, NPV, если r=10%.

Задача 3.38. Компания планирует начать производство нового продукта, который заменит устаревший. По ее расчетам для реализации проекта необходимы инвестиции в объеме 1 млн дол. в год 1. Ожидается, что новый проект принесет (после налогообложения) 250 000 дол. в год - 2, 300 000 дол. в год - 3, 350 000 дол. - в год - 4 и 400 000 дол. каждый год с 5 по 10. Хотя проект может длится и по прошествии 10 лет, но компания предпочитает быть консервативной и ограничить все расчеты этим периодом.

А. Если необходимая норма прибыли составляет 15%, чему равна чистая текущая стоимость проекта? Приемлем ли он для компании?

Б. Чему равна внутренняя норма доходности для него?

В. Как изменилась бы ситуация, если бы необходимая норма прибыли была равна 10%?

Г. Чему равен период окупаемости проекта?

Задача 3.39. Сравните по критериям NPV, IRR, DPP два проекта, если цена капитала 13%:

А. – 20000 7000 7000 7000 7000

Б. – 25000 2500 5000 10000 20000

Задача 3.40. Проект, требующий инвестиций в размере $160000, предполагает получение годового дохода в размере $30000 на протяжении пятнадцати лет. Оцените целесообразность такой инвестиции, если коэффициент дисконтирования - 15%.

Задача 3.41. Проект, рассчитанный на пятнадцать лет, требует инвестиций в размере 150000 дол. В первые пять лет никаких поступлений не ожидается, однако в последующие 10 лет ежегодный доход составит 50000 дол. Следует ли принять этот проект, если коэффициент дисконтирования равен 15%?

Задача 3.42. Ожидается, что результатом предполагаемого инвестиционного проекта, жизненный цикл которого составит 7 лет, станут следующие денежные потоки после налогов (тыс. дол.):

Год

1 10,000

2 15,000

3 15,000

4 20,000

5 15,000

6 10,000

7 5,000

а. Рассчитайте чистую текущую стоимость, если ставка дисконтирования равна 10%, 16%.

б. Определите внутреннюю норму окупаемости (доходность) предлагаемого проекта.

в. Если бы денежные потоки были одинаковыми и равными $13000 в год в течение 7 лет, какой была бы чистая текущая стоимость при ставке дисконтирования 10%?

г. Какой величины денежные потоки требуются, чтобы ставка доходности составила 16%?

д. Как изменились бы ответы на вопросы а, б, если бы в конце года происходило высвобождение капитала в сумме $10000?

е. Как изменился бы ответ на вопрос «г», если в конце года 7 происходило бы высвобождение капитала в сумме $10000?

Контрольные вопросы

1. Почему в инвестиционном анализе в качестве инструментарии в основном используется дисконтирование, а не начисление сложных процентов?

2. Поясните экономический смысл основных динамических критериев оценки (NPV, IRR, MIRR, PI, DPP).

3. Что такое чистый денежный поток, как его построить (рассчитать)?

4. Покажите особенности отражения налоговых факторов при прогнозе денежных потоков проекта.

5. Как определить величину ставки дисконтирования? В чем ее экономический смысл?

6. Какие проблемы существуют при использовании метода IRR.

7. Какие показатели следует предпочесть в условиях ограниченности капитала?

8. Что такое модифицированная внутренняя норма доходности (правила расчета и преимущества).

9. В каких случаях применяется метод индекса доходности?

10. Снимает ли расчет дисконтированного срока окупаемости проекта недостатки традиционного метода статического срока окупаемости?

11. В чем смысл точки Фишера?

12. Какие методы следует использовать при формировании оптимального инвестиционного портфеля?

Дата добавления: 2014-12-27