Точечные оценки законов распределения

Основные законы распределения.

1. Трапециидальное распределение.

К трапециидальным распределениям относятся:

1) равномерное (а); 2) собств. трапециидальное (б);

3) треугольное – Симсона (в).

2. Экспоненциальное распределение.

Наиболее распространенный вид – распределение Гаусса.

3. Уплощенное распределение – композиция равномерного и какого-либо экспоненц. распределения.

4. Семейство распределений Стьюдента.

Эти законы описывают плотность распределения вероятности среднего арифметического, вычисленного по выборке из n случайных отсчетов нормально распределенной генеральной совокупности.

Особенности:

¨ при n<3 s=¥, т.е. дисперсионная оценка ширины разброса становится невозможна;

¨ классический аппарат моментов для оценки формы и ширины распределения Стьюдента с малым числом степеней свободы (n-1) оказывается неработоспособным, их ширина и форма могут быть оценены лишь с использованием доверительной и энтропийной оценок.

5. Двухмодальное распределение.

К ним относятся:

1) дискретное двузначное (рис. а); 2) арксинусоидальное (б); 3) двухмодальные островершинные (в) и кругловершинные (г).

Остро- и кругловершинные двухмодальные распределения получаются как композиция дискретного двузначного и экспоненциального распределений с различными значениями коэффициента a (параметр распределения).

Оценка точечная, если она выражается одним числом.

Точечные оценки могут быть состоятельными, несмещенными и эффективными.

Состоятельная – оценка, которая при увеличении объема выборки стремится по вероятности к истинному значению числовой характеристики.

Несмещенная – оценка, мат. ожидание которой равно оцениваемой числовой характеристике.

Наиболее эффективной считают ту из нескольких возможных несмещенных оценок, которая имеет наименьшую дисперсию.

Точечная оценка мат. ожидания:

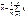
Точечная оценка дисперсии:

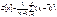
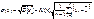
Существуют точечные оценки и других параметров.

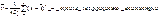
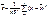
S – среднеквадратическое отклонение.

22. Интервальные оценки законов распределения: доверительный интервал, доверительная вероятность, квантильные значения погрешностей.

На практике важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с разными доверительными вероятностями находится результат измерения.

P {x_Н < x < x_В} = 1 – q

q – уровень значимости; x_Н, x_В – нижняя и верхняя границы.

Если неизвестен закон распределения, то тогда доверительный интервал находят из неравенства Чебышева

P {½x–x_y½£ tG_x} £ 1 – 1/t²

Под P-процентным квантилем x_p понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плоскости распределения равна P%.

На основании такого подхода вводится такое значение погрешности, заданной с доверительной вероятностью P – границ интервала неопределенности

±D = ±(x_p – x_1-p)/2 = ±d_p/2

Расчет доверительных интервалов для случая, когда распределение результатов наблюдения нормально, но их дисперсия неизвестна, т.е. при малом числе наблюдений n возможно выполнить с использованием распределения Стьюдента.

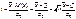
где – среднее арифметическое значение, s – СКО.

Дата добавления: 2014-12-27