Пример 1. Дисперсионный анализ

Дисперсионный анализ

Пример.

Для некоторой страны функция Лоренца имеет вид:

у (х) = 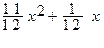. Найдем коэффициент Джини:

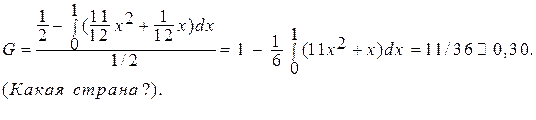
(Analysis of Variance)- ANOVA

В практической деятельности менеджеров, руководителей производств, экономических и кадровых служб часто возникает необходимость убедиться - действительно ли данный качественный фактор А оказывает существенное, значимое влияние на некоторый результативный признак.

Например, влияет ли тип станка на среднюю производительность рабочих, влияет ли температура на средний срок службы данной установки, влияет ли тот или иной месяц года на средний объем реализации продукции, влияет ли разбиение студентов на группы на их среднюю успеваемость, влияет ли размер предприятия на производительность, влияет ли численность региона на объем выручки и т.д.

Служба управления персоналом крупной компании хочет проанализировать, влияет ли тип методики обучения на среднюю производительность персонала.

Построим математическую модель ситуации и воспользуемся методом математической статистики.

1. Пусть Х - случайная величина, определяющая результативный признак, в данном случае - производительность. Фактор А - методика обучения.

2. Разобьем фактор А на к уровней - рассмотрим 3 методики обучения (к = 3) и для каждого уровня получим выборку объема n случайной величины Х (n=5):

уровень	в ы б о р к а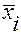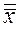

Для каждого уровня подсчитаем среднее 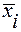, а также среднее 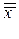по всем выборкам:

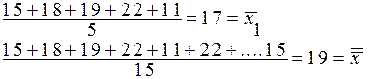
3. Подсчитываем факторную дисперсию:

(оценивает степень влияния данного фактора на результирующий признак).

Q_А = 5(17-19)² + 5(21-19)² +5(19-19)² = 40

4. Подсчитываем остаточную дисперсию:

(оценивает влияние иных, остаточных причин на результирующий признак).

Q_ост = (15-17)²+ (18-17)²+ (19-17)²+ (22-17)² + (11-17)² +

(22-21)²+ (27-21)²+ (18-21)²+ (21-21)² + (17-21)² +

(18-19)²+ (24-19)²+ (16-19)²+ (22-19)² + (15-19)² =192

Если эти дисперсии значимо отличаются, то это свидетельствует о существенном влиянии фактора, в противном случае - принимается, что фактор не оказывает существенного влияния. С целью сравнения дисперсий

5. Вычисляем значение критерия Фишера:

F_набл. =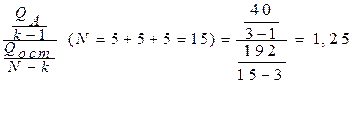

6. Выбираем уровень значимости α = 0,05

7. Находим число степеней свободы числителя (v₁) и знаменателя (v₂):

v₁ = к – 1 =2

v₂ = N– k =15 – 3=12

По таблице критерия Фишера (одна из таблиц математической статистики) находим: F_кр = 3,885

8. Так как наблюдаемое значение критерия (1,25) не превосходит критического значения (3,885), то принимается гипотеза о несущественности влияния фактора А при уровне значимости 0,05.

(в противном случае гипотезу следовало бы отвергнуть).

Дата добавления: 2014-12-27