
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Графы и их представления
|
|
|
|
Граф — это множество точек, называемых вершинами, и множество линий, называемых ребрами, которые соединяют пары вершин, или вершину саму с собой, в виде дуги. Простейшей аналогией графа является карта, на которой нанесены города (вершины), а дороги (ребра, дуги) соединяют их. Для математических целей мы нуждаемся в более строгом определении. Чтобы определить граф, мы должны корректно задать множество вершин и множество ребер. Далее мы должны четко указать, какие ребра соединяют какие вершины. По определению ребро должно иметь вершину на каждом своем конце, поэтому каждому ребру графа мы должны приписать его вершины на концах, то есть каждое ребро е мы определяем как множество пар вершин {v1, v2}, которые е соединяет. Таким образом, множество {v1, v2}, которое мы будем обозначать 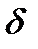 (е), представляет собой подмножество множества вершин. Следовательно,
(е), представляет собой подмножество множества вершин. Следовательно, 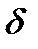 (е) это элемент мощностного множества вершин. Итак, мы приходим к следующему формальному определению.
(е) это элемент мощностного множества вершин. Итак, мы приходим к следующему формальному определению.
Определение 1.1. Ненаправленный граф Г это:
(i) конечное множество V вершин;
(ii) конечное множество Е ребер;
(iii) функция 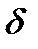 : Е
: Е  P(V) такая, что для каждого ребра е,
P(V) такая, что для каждого ребра е, 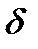 (е) одно или двух элементное подмножество множества V.
(е) одно или двух элементное подмножество множества V.
Говорят, что ребра е связывают элементы (элемент) 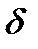 (е). Рассмотрим например, граф Г, представленный на рис. 1.
(е). Рассмотрим например, граф Г, представленный на рис. 1.
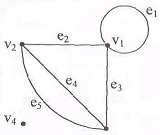
Рис. 1. Пример графа Г
Здесь для графа Г множество вершин будет: {v1, v2, v3, v4}, множество peбep {e1, e2, e3, e4, e5}. Функция 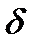 : Е
: Е 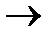 P(V) определена так:
P(V) определена так:
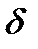 : e1
: e1 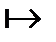 {v1};
{v1};
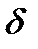 : e2
: e2 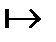 {v1, v2};
{v1, v2};
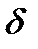 : e3
: e3 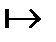 {v1, v3};
{v1, v3};
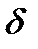 : e4
: e4 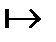 {v2, v3};
{v2, v3};
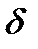 : e5
: e5 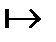 {v2, v3}.
{v2, v3}.
В данном случае ребро е1 связывает вершину v1 саму с собой. Ребро е2 связывает вершину v1 с вершиной v2, и т.д., вершина v4 оказывается не связанной ни с какой другой вершиной, вершины v1 и v3 связаны не одним, а двумя ребрами е4 и е5.
К сожалению, существует много различных подходов к определению графа. Отдельные авторы при определении графа исключают возможность введения нескольких ребер, соединяющих одни и те же вершины, другие исключают возможность наличия петель, то есть ребер, соединяющих вершину саму с собой, а потом, чтобы определить данные графы вводятся специальные термины типа мультиграф и т.п. Таким образом, в настоящее время все еще не сложилось единого стандарта терминологии теории графов, поэтому, если вы открываете новую книгу, то внимательно проследите за введенными автором понятиями и определениями.
Следует обратить также внимание не тот факт, что граф и диаграмма, его представляющая, это не одно и то же. Как мы определили, граф состоит из двух множеств и функции. Рис. 1 — это не граф, это наглядное представление одного из них. Несмотря на то, что представление графа в виде диаграммы оказывается очень полезным для наглядного восприятия свойств графа, здесь нужна определенная осторожность. Дело в том, граф может быть представлен несколькими диаграммами, которые сильно отличаются друг от друга. Такой пример приведен на рис. 2. Граф Т, изображенный на рис. 2.(а), называют графом колеса с семью вершинами W7. В общем случае Wn.
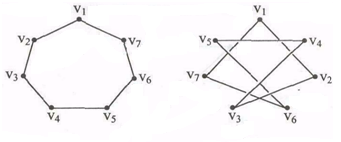
а) б)
Рис. 2. Две диаграммы одного графа Т: а – граф колеса; б – другое представление графа Т
.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 509; Нарушение авторских прав?; Мы поможем в написании вашей работы!