Определение 1.3

Определение 1.2.

(i) Пара вершин v и w называются смежными, если существует ребро е, соединяющее их. В таком случае говорят также, что вершины v, w инцидентны ребру е или также ребро е инцидентно вершине v и вершине w.

(ii) Ребра е„ е₂,..., е„ называются смежными, если они имеют, по крайней мере, одну общую вершину.

(iii) Валентностью или степенью вершины v / (v)/ называется число и ребер инцидентных вершине v. (Если не оговаривается особо, петля учитывается дважды при подсчете валентности вершины v) Граф, у которого каждая вершина имеет одинаковую валентность r, называется правильным (с валентностью r) или просто r-валентным графом.

Пример 1.1. Рассмотрим граф, изображенный на рис. 1. Вершины v₁, v₂ смежные, ибо ребро е₂ связывает их. Аналогично вершины v₁, v₃ смежные, v₂, v₃ - смежные. Только вершина v₄ не будет смежной ни по отношению ни к одной другой вершине. Ребра e_l е₂, е₃ смежные, так как все они соединяются в вершине v₁. Аналогично ребра е₂, е₄, е₅ смежные, и ребра e₃, e₄, e₅ смежные. Отметим, что только пары вершин могут быть смеж­ными, а число смежных ребер может быть любым. Валентности четырех вершин приведены в табл. 1.

Таблица 1.

Валентность вершин графа Г, изображенного на рис. 1

Вершина	Валентность
v1
v2
v3
v4

(i) Нулевым графом (или полностью несвязанным графом) называется граф с пустым множеством ребер, то есть нулевой граф — это просто множество точек (вершин).

(ii) Полным графом называется граф, у которого каждая пара различных вершин связана ровно одним ребром.

(iii) Двудольным графом называется граф, у которого множество вершин имеет разбиение {V₁, V₂} такое, что каждое ребро связывает вершины из множества V₁ с вершиной из множества V₂.

(iv) Полным двудольным графом называется двухдольный граф, у которого каждая вершина множества V₁ связана с каждой вершиной множества V₂ единственным ребром.

(v) Простым графом мы называем граф, который не имеет петель или множественных ребер, то есть для того, чтобы назвать граф простым не должно быть двух ребер, соединяющих одну и туже пару вершин и не должно быть ребер, соединяющих вершину саму с собой.

Пример 1.2. Так как полный граф — это простой граф, то у полного графа нет петель, и каждая пара различных вершин соединена единственным ребром. Поэтому полный граф однозначно задается числом своих вершин.

Полный граф К_n с n вершинами может быть описан так: К_n имеет множество вершин V = {v₁, v₂,..., v_n} и множество ребер Е = {е_ij: 1 i < j 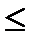n} с функцией 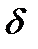(е_ij) = {v_i, v_j}.

Очевидно, что граф К_n является правильным с валентностью (n-1), так как каждая вершина связана с каждой из остальных (n-1) вершин посредством одного ребра. Полные графы с тремя, четырьмя и пятью вершинами показаны на рис. 3.

Рис. 3. Полные графы К_n

Пример 1.3. Пусть Г — двудольный граф и его множество вершин V имеет разбиение {V₁,, V₂}- Отметим, что Г не обязан быть простым. Все, что требуется это каждое ребро должно соединять вершины множества V₁ с вершинами множества V₂. Для заданных вершин v₁ 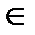V, и v₂ V₂ может быть более, чем одно ребро, соединяющие их или вообще не быть ни одного ребра, соединяющего вершины V ₁ и V₂. Понятно, что такой граф Г не должен иметь петель. Полный двудольный граф полностью описывается числом вершин своих частей, то есть числами | V₁|=n, |V₂|=m.

Полный двудольный граф с числом вершин n, m обозначается К_n,m где. IV₁|=n, |V₂|=m. Он, конечно, является простым.

На рис. 4. показаны два двудольных графа. В каждом случае вер­шины множества V₁ обозначены кружком, а вершины множества V₂ крестиком. Граф K_3,3 на рис. 4 - это полный двудольный граф

Рис. 4. Двудольные графы

Мы уже отмечали, что граф Г может быть представлен с помощью диаграмм, которые могут сильно отличаться друг от друга даже для одного графа. Альтернативный способ представления графа, очень удобный, кстати, для компьютерного представления это представле­ние графа с помощью "матрицы смежности".

Определение 1.4. Пусть Г - граф с множеством вершин {v₁, v₂,.., v_n}. Матрицей смежности графа Г называется матрица nxn А=А(Г), элементы которой а_ij представляют собой число различных ребер, соединяющих вершины v_i и v_j.

Матрицы смежности с неизбежностью должны быть симметричными, так как число ребер, соединяющих вершины v_i и v_j, равно числу ребер, соединяющих вершины v_j и v_i. Валентность вершины v_i можно легко определить на основании матрицы смежности. Если у графа Г нет петель при вершине v_i, то валентность этой вершины равна сумме всех элементов i-ой строки (или i-oro столбца). Так как каждая петля учитывается дважды при вычислении валентности, то при суммировании элементов i-ой строки (или i-oro столбца) элемент диагонали а_ii должен быть удвоен при вычислении валентности вершины v_i.

Пример 1.4. Запишем матрицу смежности А для графа, представленного на рис. 1.

.

Заметим, что V = {v₁, v₂, v₃, v₄} и строки и столбцы матрицы А соответствуют порядку следования элементов множества V. Две особенности данного графа могут быть сразу отмечены. Во-первых, на главной диагонали имеется только один элемент а_ii = 1, отличный от нуля, поэтому граф имеет только одну петлю при вершине v₁. Во-вторых, последняя строка (столбец) состоит только из нулей, то есть вершина v₄является изолированной, она не связана ни с одной другой вершиной. Валентность вершин может быть легко определена на основе матрицы смежности:

(v₁) = 2x1+1+1 = 4
(v₂) = 1+2 = 3
(v₃) = 1+2 = 3
(v₄) = 0

Пример 1.5. Нулевой граф, содержащий "n" вершин, имеет матрицу смежности nхn, которая состоит только из нулей О_nхn.

Пример 1.6. Полный граф имеет матрицу смежности, которая имеет нули на главной диагонали (так как не должно быть петель) и во всех остальных местах единицы (так как каждая вершина должна быть связана с любой другой один раз).

Таким образом, граф можно задать:

- перечислением конечного множества вершин, конечного множества ребер и функцией соответствия элементов множества вершин и ребер

- матрицей смежности;

- диаграммой.

Дата добавления: 2014-12-27