Деревья. Интуитивно понятно, что отдельные графы могут состоять из раз­розненных блоков, в то время как другие оказываются локализованны­ми в единый комплекс. Мы можем

Связность

Интуитивно понятно, что отдельные графы могут состоять из раз­розненных блоков, в то время как другие оказываются локализованны­ми в единый комплекс. Мы можем воспользоваться понятием пути, чтобы сформулировать данные обстоятельства более точно.

Определение 1. 6. Граф называется связным, если для любой пары различных вершин существует соединяющий их путь.

Произвольный граф естественно разбивается на некоторое число связных подграфов, которые называются компонентами связности.

Как правило, из диаграммы графа всегда можно сказать, сколько компонент он имеет. Иногда это сразу видно, а иногда требуется более внимательный анализ. Граф, представленный на рис. 1, имеет две компоненты связности, одна из которых — это нулевой граф с вершиной {v₄}.

Выше мы рассмотрели пути и циклы графа. Существует специальный тип графа, называемый «дерево», который вообще не имеет циклов. Впервые ввел понятие деревьев физик Густав Кирхгофф в 1847. Будучи студентом Кенигсбергского университета, он сформулировал законы, управляющие течением тока в электрических сетях. Сети проводов могут быть рассмотрены, как графы. Уравнения, которые вытекают из законов Кирхгоффа, не являются незави­симыми и Кирхгофф использовал деревья для получения независимого подмножества уравнений.

В последние десятилетия компьютерная наука столкнулась с тем фактом, что деревья обеспечивают удобные структуры для хранения и исправления определенных типов данных - так называемых иерархи­ческих баз данных.

Определение 3.7. Дерево- это связанный граф, который не содержит циклов.

Из определения сразу ясно, что деревья не имеют петель или кратных ребер. Каждая петля является цепью и если ребра е_i и e_j соединяют одну пару вершин, то последовательность е_i, e_j будет циклом.

На рис. 5 приведены примеры деревьев.

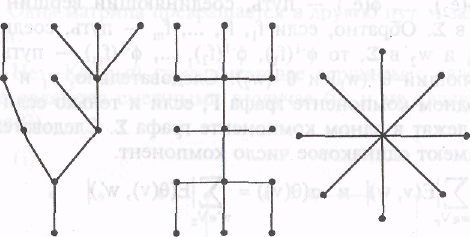
Рис. 5. Деревья

Одна из причин, по которой деревья имеют большое значение в прикладных задачах, связана с тем, что любой связнный граф содержит в себе дерево, которое называется деревом по­крытия покрывающим деревом или остовным деревом, которое связывает все вершины графа. Помимо этого дерево покрытия обеспечивает удобное множество путей, связывающих любые пары вершин графа,

Определение 1.8. Пусть Г- связный граф с множеством вершин V. Деревом покрытия графа Г называется подграф, который является деревом, и множеством вершин которого является множество V.

Теорема 1.1. Каждый связный граф содержит в себе покрывающее дерево.

Доказательство: Пусть Г — связный граф; если Граф не, содержит циклов, то доказывать ничего не надо, ибо Г сам по себе - дерево покрытия. Предположим, что Г содержит цикл. Удаление любого ребра из цикла дает граф, который все еще остается связным. Если новый граф все еще содержит циклы, то опять удалим одно ребро этого цикла. Продолжим процесс до тех пор, пока результирующий граф Г не будет содержать ни одного цикла. Мы не удалили ни одной вершины, поэтому граф Г имеет такое же множество вершин, как и граф Г, и на каждой стадии процесса обрезания цикла связность графа не нарушалась. Итак, граф Г - связный и представляет собой дерево покрытия графа Г.

Заметим, что исходный связный граф Г, в общем случае может иметь много различных деревьев покрытия.

Простая структура деревьев позволяет нам легко получить некоторые элементарные положения с ними связанные, которые сформули­рованы в виде следующей теоремы.

ТЕОРЕМА 1.2. Пусть Т - дерево с множеством вершин V и множеством ребер Е. Тогда:

(i) для каждой пары различных вершин v и w существует единственный путь в Т, связывающий их;

(ii) удаление любого ребра из Т приводит к образованию графа с двумя компонентами, каждая из которых является деревом;

(ii) |E|=|V| – 1

Более того, связанный граф, удовлетворяющий любому одному из этих свойств, является деревом.

Доказательство:

(i) Пусть v и w — любые две различные вершины графа Т; так как Т - связанный граф, то существует путь Р₁ е₁, е₂,..., е_n связывающий v и w. Предположим, что существует другой путь Р₂: f₁, f₂,..., f_m, который также связывает v и w. В некоторой точке эти два пути должны расходиться. Пусть v* - является последней вершиной, до которой, перед началом расхождения, пути p₁ и Р₂ имели общую часть. Так как оба пути заканчиваются на вершине w, то эти пути должны опять соединиться. Пусть w* - первая вершина, в которой пути Р₁ Р₂ сходятся (см. рис. 6). Определим путь так: берем ребра пути Р₁, связывающие v* и w* и присоединяем ребра пути Р₂, связывающие w* и v*. Такой путь связывает вершину v* саму с собой без повторения ребер, то есть это цепь графа Т. Однако, этого не может быть, ибо Т - дерево. Следовательно, существует только единственный путь, связывающий v и w.

Рис. 6. Связанный граф Т

(ii) Пусть "е" - произвольное ребро графа Т, связывающее вершины v и w и пусть Г- граф, получаемый путем удаления ребра "е" из графа Т. Так как ребро "е" представляет собой единственный путь графа Т, связывающий v и w, то у графа Г нет пути, связывающего вершины v и w, то есть Г - несвязный.

Пусть V₁ - множество вершин графа Г, которые могут быть связаны путем графа Г с вершиной v и пусть V₂ - множество вершин графа Г, которые могут быть связаны путем графа Г с вершиной w. Тогда V₁ V₂ = V и V₁, V₂ определяют два связных подграфа графа Г. Каждая из этих компонент графа Г является деревом, ибо любая цепь в какой -либо из компонент была бы также цепью графа Т.

(iii) Доказывается по индукции числа вершин графа Т.

Теперь докажем, что если Г - связный граф, удовлетворяющий свойству (i) или (ii), то Г- дерево.

Начнем с первого. Пусть Г - связный граф и пусть Г удовлетворяет (i). Если у графа Г имеется цикл, содержащий пару различных вершин v и w, то этот цикл обеспечивает существование двух различных путей, связывающих v и w. Так как это противоречит условию (i), то таких циклов нет. Не будет также и петель у графа Г. Если V-петля при вершине v и w - любая другая вершина, то существует два различных пути, связывающих v и w: один путь начинается с "е", а другой нет. Следовательно, если Г вообще не содержит циклов, то Г- дерево.

Наконец, предположим, что Г - связный граф и выполняется свой свойство (ii). Если Г содержит цикл, то мы можем удалить ребро цикла, не нарушая связанности Г, что противоречит (ii). Следовательно, опять Г вообще не должен содержать циклов и поэтому Г является деревом.

Дата добавления: 2014-12-27